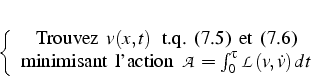6.2 Formulation faible

La formulation faible de l'équation des ondes (7.3) s'obtiens classiquement en multipliant par une fonction test $w(x)=\delta v$ (variation de $v(x,t)$ à un instant t fixé), et en intégrant l'équation à $t$ fixé sur le domaine de calcul:

$$\int_{0}^{L}\frac{\partial^{2}v}{\partial t^{2}}w dx=\int_{0}^{L}c_{0}^{2}\frac{\partial v^{2}}{\partial x^{2}}w dx$$

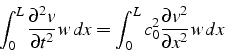
En intégrant par partie le membre de droite, et en utilisant les conditions aux limites de Dirichlet sur $v$ (7.5), qui imposent des conditions homogènes sur la variation $w$

$$w(0)=0 \mbox{et } w(L)=0$$

on obtiens la formulation faible suivante:

$$% latex2html id marker 11253\left\{ \begin{array}{c} \mbox... ...forall w(x) \mbox{ t.q. } w(0)=w(L)=0\end{array}\right.$$ (6.7)

Cette formulation faible correspond au thèorème des travaux virtuels, qui traduit la condition de minimisation de l'action $\mathcal{A}=\int_{0}^{\tau}\mathcal{L}(v,\dot{v}) dt$, avec un Lagrangien:

$$\mathcal{L}(v,\dot{v})=\underbrace{\frac{1}{2}\int_{0}^{L}\l... ...l v}{\partial x}\right)^{2}dx}_{U=\mbox{énergie potentielle}}$$

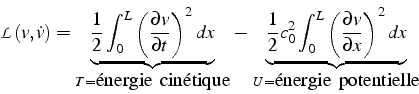
La formulation variationnelle associée s'écrit alors:

$$% latex2html id marker 14071\left\{ \begin{array}{c} \mbox... ...A}=\int_{0}^{\tau}\mathcal{L}(v,\dot{v}) dt\end{array}\right.$$