suivant: 6.2 Formulation faible monter: 6. Problème hyperbolique: modes précédent: 6. Problème hyperbolique: modes Table des matières
Considérons une corde tendue suivant l'axe ![]() , initialement au
repos avec une longueur
, initialement au
repos avec une longueur ![]() et soumise à une tension
et soumise à une tension ![]() 6.1, que l'on déforme à l'instant
6.1, que l'on déforme à l'instant ![]() . C'est le problème de la corde
pincée d'un instrument de musique (clavecin), dont on se propose d'étudier
la vibration (figure 7.1).
. C'est le problème de la corde
pincée d'un instrument de musique (clavecin), dont on se propose d'étudier
la vibration (figure 7.1).
On suppose que la corde est sans raideur (ou souple), c'est à dire
que la résultante des contraintes est la tension ![]() qui reste
tangente à la corde. On néglige en particulier le moment de flexion
qui apparaıt si la corde possède une raideur (cas d'une poutre). On
tiens cependant compte de l'élasticité de la corde, qui peut s'allonger
proportionnellement à une variation de tension.
qui reste
tangente à la corde. On néglige en particulier le moment de flexion
qui apparaıt si la corde possède une raideur (cas d'une poutre). On
tiens cependant compte de l'élasticité de la corde, qui peut s'allonger
proportionnellement à une variation de tension.
Considérons un élement de corde ![]() de longueur
de longueur ![]() (figure 7.1)
situé en un point
(figure 7.1)
situé en un point ![]() de la corde. Au repos ce brin de corde
de la corde. Au repos ce brin de corde ![]() est situé au point
est situé au point ![]() d'abscisse
d'abscisse ![]() , d'ordonnée
, d'ordonnée ![]() et
a pour longueur
et
a pour longueur ![]() :
: ![]()
A l'instant ![]() il a subit un déplacement longitudinal
il a subit un déplacement longitudinal ![]() et un déplacement transversal
et un déplacement transversal ![]() . Le point
. Le point ![]() se trouve donc
en
se trouve donc
en ![]() et
et ![]() :
: ![]() et le point
et le point ![]() en
en ![]() et
et
![]() :
:
![]() . Le brin
. Le brin ![]() fait un angle
fait un angle ![]() avec l'axe
avec l'axe ![]() et sa longueur
et sa longueur ![]() vaut donc
vaut donc
![]() ,
soit puisque les variables ne dépendent que de
,
soit puisque les variables ne dépendent que de ![]() et du temps
et du temps ![]() :
:
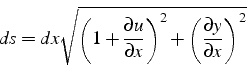
L'angle ![]() vérifie les relations suivantes:
vérifie les relations suivantes:
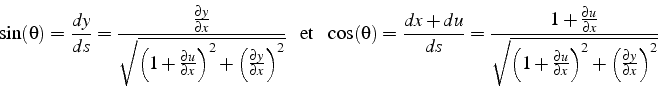
Pour de petits déplacements (
![]() , et à un instant
, et à un instant
![]() fixé on en déduit les relations suivantes:
fixé on en déduit les relations suivantes:
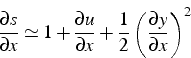
L'allongement relatif du brin ![]() s'écrit:
s'écrit:
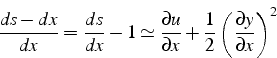
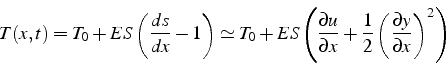
L'équation d'équilibre dynamique pour le brin ![]() de masse volumique
de masse volumique
![]() :
:
En ne conservant que les termes du premier ordre (petites oscillations), on obtiens un système de 2 équations découplées :
qui sont 2 équations des ondes, correspondant respectivement à des
ondes de flexion ( ![]() ) de célérité
) de célérité
![]() et des ondes de compression (
et des ondes de compression (![]() ) de célérité
) de célérité
![]() .
.
Dans la cas d'une corde de section ![]() constante, ces 2 équations
s'écrivent sous la forme d'une équation des ondes avec une célérité
constante
constante, ces 2 équations
s'écrivent sous la forme d'une équation des ondes avec une célérité
constante ![]() (
(![]() ou
ou ![]() ):
):
Dans le cas d'une corde de section ![]() non constante (de section
moyenne
non constante (de section
moyenne ![]() ), cette équation s'écrit:
), cette équation s'écrit:
avec
![]() ,
, ![]() et
et
![]() pour l'onde de flexion
pour l'onde de flexion ![]() et
et
![]() ,
, ![]() et
et
![]() pour l'onde de compression
pour l'onde de compression
![]() .
.
A cette équation on ajoutte des conditions aux limites de déplacement nul aux 2 extrémitées:
et des conditions initiales (déformation ![]() sans vitesse
initiale):
sans vitesse
initiale):