suivant: 2.4 Remarques finales monter: 2. Les équations de précédent: 2.2 Équation de bilan Table des matières
La résolution numérique des équations d'équilibre précédentes nécessitent des informations supplémentaires (conditions aux limites et/ou initiales). Le choix et le type de ces conditions sont importantes et conditionnent souvent la résolution numérique. De ce point de vue, nous distinguerons 3 grandes classes de problème.
Cette classe de problèmes corresponds à des problèmes stationnaires, qui sont caractéristiques de:
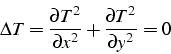
Pour résoudre cette équation dans un domaine ![]() , il faut se
donner une condition aux limites 2.1en tous les points de la frontière
, il faut se
donner une condition aux limites 2.1en tous les points de la frontière
![]() . Cette
condition aux limites peut être une:
. Cette
condition aux limites peut être une:
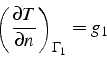
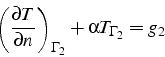
Pour des équations d'ordre 4 (2.16), l'équation type est le bi-laplacien :

Pour résoudre cette équation dans un domaine ![]() , il faut se
donner deux conditions2.2 aux limites en chaque point de la frontière
, il faut se
donner deux conditions2.2 aux limites en chaque point de la frontière
![]() . Ces 2 conditions peuvent être une combinaison de
. Ces 2 conditions peuvent être une combinaison de
Cette classe de problèmes corresponds à des problèmes instationnaires, qui sont caractéristiques de:
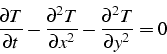
Pour résoudre cette équation dans un domaine ![]() , il faut se
donner une condition aux limites en chaque point de la frontière
, il faut se
donner une condition aux limites en chaque point de la frontière
![]() (comme pour les problèmes elliptiques) et une condition initiale:
la valeur de la solution à
(comme pour les problèmes elliptiques) et une condition initiale:
la valeur de la solution à ![]() .
.
Cette classe de problèmes corresponds à des problèmes instationnaires, qui sont caractéristiques de:
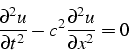
qui nécessite pour la résoudre 2 conditions initiales: la valeur de la solution et de sa dérivée temporelle à l'instant initial, et des conditions aux limites.
Dans le cas de système hyperbolique (2.19,2.20), il faut se donner une condition initiale, mais les conditions aux limites sont plus délicates à formuler et dépendent des ondes caractéristiques qui peuvent se propager dans le milieu.