2.1 Equation de bilan pour un champ scalaire

En mécanique des milieux continus, l'équation d'évolution d'une quantité physique $W(t,x,y,z)$ par unité de masse (température, concentration, énergie ...) traduit un principe de conservation, et donc un bilan effectué sur un petit élément de volume $dV=dxdydz$ fixe par rapport à l'observateur (formulation eulérienne). En notant $\rho$, la masse volumique du milieu, la quantité de $W$ dans l'élément $dV$ est $\rho WdV$. La variation temporelle de $W$est donc égale à la somme des fluxs de $W$ à travers les facettes $dS$ auquelle on ajoutte les termes sources volumiques $T_{s}$.

L'équation de bilan peut s'écrire sous forme générique:

$$\underbrace{\frac{\partial}{\partial t}(\rho W)dV}_{\mbox{va... ...dS\right)}_{\mbox{fluxs}}+\underbrace{T_{s}dV}_{\mbox{source}}$$ (2.1)

Cette équation contient

1. un terme instationnaire $\frac{\partial\rho W}{\partial t}$,
2. des termes de flux surfaciques $\phi$, traduisant un bilan à travers les surfaces $dS$ du volume $dV$,
3. des termes sources volumiques $T_{s}$.

Pour les fluxs, on distingue des fluxs par diffusion moléculaire $\phi_{d}$, qui sont proportionnels au gradient de $W$ dans la direction normale à la facette $dS$: $\phi_{d}=\lambda\frac{\partial W}{\partial n}$ (loi de Fourier), et des flux de convection $\phi_{c}$, qui traduisent le transport de $W$ par le milieu et sont proportionnels à la vitesse $\overrightarrow{\mathbf{V}}$ dans la direction normale à la facette $dS$: $\phi_{c}=\rho W \overrightarrow{\mathbf{V}}.\overrightarrow{n}$

En considérant un milieu homogène suivant l'axe $z$ , avec un champ de vitesse bidimensionnel $\overrightarrow{V}=(v_{1},v_{2})$ (figure 2.1), le bilan (2.1) s'écrit:

Figure 2.1: bilan de flux sur un élément de volume (en 2D)

$$\begin{eqnarray*} \frac{\partial\rho W}{\partial t}dxdydz & = & \left(\left(\lam... ...+\left(v_{2}\rho W\right)_{y}\right)dxdz\\ & + & T_{s}(W)dxdydz\end{eqnarray*}$$

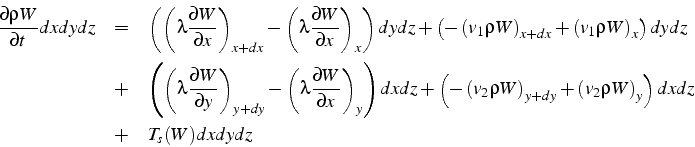
En effectuant les développements limités des termes en $x+dx$ et $y+dy$ et un passage à la limite, on obtiens l'équation classique de bilan pour un scalaire $W$:

$$\frac{\partial\rho W}{\partial t} = \frac{\partial}{\partial x}(\lambda\frac{\partial W}{\partial x})... ...ial}{\partial x}(\rho v_{1}W)-\frac{\partial}{\partial y}(\rho v_{2}W)+T_{s}(W)$$ (2.2)

$$= div(\lambda \overrightarrow{grad }W)-div(\overrightarrow{\mathbf{V}}\rho W)+T_{s}(W)$$

Cette équation (2.2) est l'équation classique de convection diffusion. A partir de cette équation, on retrouve les équations classiques en mécanique des milieux continus:

1. équation de diffusion pure:
   
   

   $$div(\lambda \overrightarrow{grad}W)=0$$ (2.3)

   
   
   l'exemple type est l'équation de la chaleur stationnaire, qui donne la répartition stationnaire de la température dans un solide homogène:
   
   

   $$\Delta T=\frac{\partial^{2}T}{\partial x^{2}}+\frac{\partial^{2}T}{\partial y^{2}}=0$$ (2.4)

   
   

2. équation de diffusion instationnaire:
   
   

   $$\frac{\partial\rho W}{\partial t}=div(\lambda \overrightarrow{grad}W)$$ (2.5)

   
   
   l'exemple type est l'équation de la chaleur instationnaire, qui traduit l'évolution temporelle de la température dans un solide homogène:
   
   

   $$\frac{\partial T}{\partial t}=K\Delta T=K(\frac{\partial^{2}T}{\partial x^{2}}+\frac{\partial^{2}T}{\partial y^{2}})$$ (2.6)

   
   

3. équation de convection pure:
   
   
   $$\frac{\partial\rho W}{\partial t}+div(\overrightarrow{\mathbf{V}}\rho W)=0$$
   
   
   l'exemple type est l'équation de transport, qui traduit le transport d'un scalaire $C$ par le champ de vitesse d'un fluide incompressible ($\rho=cste$, $div\overrightarrow{\mathbf{V}}=0$):
   
   
   $$\frac{\partial C}{\partial t}+\overrightarrow{\mathbf{V}} \overrightarrow{grad}C=0$$
   
   

4. équation de diffusion convection:
   
   

   $$\frac{\partial\rho W}{\partial t}+div(\overrightarrow{\mathbf{V}}\rho W)=div(\lambda \overrightarrow{grad}W)$$ (2.7)

   
   
   l'exemple type est l'équation de convection diffusion de la température dans un fluide incompressible ($\rho=cste$, $div\overrightarrow{\mathbf{V}}=0$):
   

   $$\frac{\partial T}{\partial t}+\overrightarrow{\mathbf{V}} \overrightarrow{grad} T=K\Delta T$$ (2.8)