2.2 Équation de bilan pour un champ vectoriel

Le principe fondamental de la dynamique, qui traduit l'équilibre entre l'accélération et les forces appliquées, conduit lorsqu'on l'applique à un élément de volume à une équation de bilan vectorielle. Cette équation de bilan a cependant une forme différente suivant la variable vectorielle choisie pour décrire le mouvement.

2.2.1 Équation de bilan local en mécanique des solides

En mécanique des solides, la variable choisie est le champ de déplacement $\overrightarrow{U}$. L'accélération d'un élément de volume de masse $\rho dV$ , qui s'écrit $\vec{\gamma}=\frac{\partial^{2}\vec{U}}{\partial t^{2}}$ , est égale à la somme des contraintes $\overrightarrow{\sigma}.\overrightarrow{n}$ (avec une composante normale $\sigma$ et une composante tangentielle $\tau$) qui s'exercent sur les facettes $ds$, auquelle on ajoutte les forces volumiques $\overrightarrow{f}$.

Cette équation de bilan s'écrit:

$$\rho\frac{\partial^{2}\overrightarrow{U}}{\partial t^{2}}dV=... ...arrow{\sigma}.\overrightarrow{n} dS +\overrightarrow{f} dV$$

Figure 2.2: bilan des forces sur un élément de solide (en 2D)

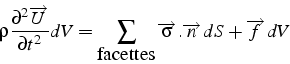
Pour un problème plan (figure ), ce bilan s'écrit sous la forme de 2 équations scalaires:

$$\begin{eqnarray*} \rho dxdydz\frac{\partial^{2}u_{1}}{\partial t^{2}} & = & \lef... ...ht)dxdz+\left(\tau_{xy}(x+dx)-\tau_{xy}(x)\right)dydz+f_{2}dxdydz\end{eqnarray*}$$

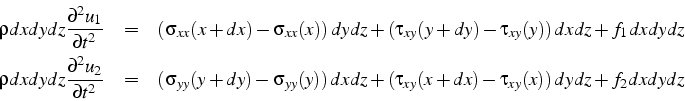
En effectuant des développements limités et après une passage à la limite, on obtiens les équations d'équilibre:

$$\begin{eqnarray*} \rho\frac{\partial^{2}u_{1}}{\partial t^{2}} & = & \frac{\part... ...au_{xy}}{\partial x}+\frac{\partial\sigma_{yy}}{\partial y}+f_{2}\end{eqnarray*}$$

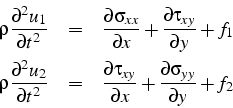
soit sous forme vectorielle:

$$\rho\frac{\partial^{2}\overrightarrow{\mathbf{U}}}{\partial ... ...arrow{\mathbf{div}} \overrightarrow{\sigma}+\overrightarrow{f}$$

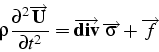
La loi de comportement du matériau permet d'obtenir la relation entre les contraintes $\overrightarrow{\sigma}$ et les déformations $\overrightarrow{\varepsilon}$. En élasticité linéaire, cette relation s'écrit:

$$\overrightarrow{\sigma}=\mathbf{D} \overrightarrow{\varepsilon}$$

où $\mathbf{D}$ est la matrice des propriétés du matériau. Pour un matériau homogène et isotrope, en notant $E$ le coefficient d'élasticité et $\nu$ le module d'Young du matériau, cette relation s'écrit:

$$\left[\begin{array}{c} \sigma_{xx}\\ \sigma yy\\ \sigma zz... ..._{xy}\\ \varepsilon_{yz}\\ \varepsilon_{zx}\end{array}\right]$$

Dans le cas d'un champ de contrainte plane $(\sigma_{zz}=\tau_{yz}=\tau_{zx}=0)$, la relation se simplifie puisque $\varepsilon_{zz}=-\frac{\nu}{1-\nu}(\varepsilon_{xx}+\varepsilon_{yy})$

$$\begin{eqnarray*} \left[\begin{array}{c} \sigma_{xx}\\ \sigma_{yy}\\ \tau_{xy}... ...on_{xx}\\ \varepsilon_{yy}\\ \varepsilon_{xy}\end{array}\right]\end{eqnarray*}$$

Dans le cas d'un champ de contrainte unidimensionnel $(\sigma_{yy}=\tau_{xy}=0)$, on retrouve les relations classiques de la résistance des matériaux, en utilisant $\varepsilon_{yy}=-\nu \varepsilon_{xx}$:

$$\sigma_{xx}=E \varepsilon_{xx}$$

La relation cinématique lie le champ de déformation $\overrightarrow{\varepsilon}$ au champ de déplacement $\overrightarrow{U}$:

$$\varepsilon_{xx}=\frac{\partial u_{1}}{\partial x}\„ \tau_... ...tial x})\„ \varepsilon_{yy}=\frac{\partial u_{2}}{\partial y}$$

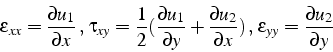
A partir de ces équations d'équilibres, on retrouve les équations classiques

1. équation de traction en statique:
   qui traduit l'équilibre d'une poutre en traction-compression unidimensionnel
   

   $$E\frac{\partial u_{1}^{2}}{\partial x^{2}}=0$$ (2.9)

   
   

2. équation de traction en dynamique:
   qui modélise les vibrations libres d'un poutre en traction-compression
   

   $$\rho\frac{\partial^{2}u_{1}}{\partial t^{2}}=E\frac{\partial u_{1}^{2}}{\partial x^{2}}$$ (2.10)

   
   

3. équations couplées en statique:
   qui traduisent l'équilibre d'une plaque en traction
   
   

   $$\frac{E}{1-\nu^{2}}\left(\frac{\partial}{\partial x}\left(\frac{\... ...rtial u_{1}}{\partial y}+\frac{\partial u_{2}}{\partial x}\right)\right)\right) = 0$$ (2.11)

   $$\frac{E}{1-\nu^{2}}\left(\frac{\partial}{\partial y}\left(\frac{\... ...rtial u_{1}}{\partial y}+\frac{\partial u_{2}}{\partial x}\right)\right)\right) = 0$$

   
   

4. équations couplées en dynamique:
   qui modélisent les vibrations libres d'une plaque en traction-compression
   

   $$\rho\frac{\partial^{2}u_{1}}{\partial t^{2}} = \frac{E}{1-\nu^{2}} \frac{\partial}{\partial x}\left(\frac{\partial u_{1}}{\partial x}+\nu\frac{\partial u_{2}}{\partial y})\right)$$ (2.12)

   $$+ \frac{E}{2(1+\nu)} \frac{\partial}{\partial y}\left(\frac{\partial u_{1}}{\partial y}+\frac{\partial u_{2}}{\partial x}\right)$$ (2.13)

   $$\rho\frac{\partial^{2}u_{2}}{\partial t^{2}} = \frac{E}{1-\nu^{2}} \frac{\partial}{\partial y}\left(\frac{\partial u_{2}}{\partial y}+\nu\frac{\partial u_{1}}{\partial x})\right)$$

   $$+ \frac{E}{2(1+\nu)} \frac{\partial}{\partial x}\left(\frac{\partial u_{1}}{\partial y}+\frac{\partial u_{2}}{\partial x}\right)$$ (2.14)

   
   

2.2.2 Équations de bilan moyennées en mécanique des solides

Pour un certain nombre de problèmes de mécanique des solides, on peut simplifier l'approche locale précédente en moyennant les efforts sur un volume moyen, par exemple une section de poutre.

Figure 2.3: poutre en flexion

Ainsi pour une poutre en flexion, on peut utiliser les hypothèses de Bernouilli (les sections restent planes, orthogonales à la ligne moyenne et conservent leur forme). Dans une section $S$ la résultante des efforts se réduit alors à une force de cisaillement $T$ et un moment fléchissant $M_{z}$:

$$T=\int_{S}\sigma_{xy}dS \mbox{ et } M_{z}=\int_{S}y\sigma_{xx}dS$$

L'équilibre des forces sur le volume entre 2 sections soumis à une charge linéique $p$ (suivant y) s'écrit:

$$M_{z}(x+dx)=M_{z}(x)+Tdx \mbox{ et } T(x+dx)=T(x)+pdx$$

soit par passage à la limite:

$$\frac{dM_{z}}{dx}=T, \frac{dT}{dx}=p$$

ce qui fournit l'équation d'équilibre:

$$\frac{dM_{z}^{2}}{dx^{2}}=p$$ (2.15)

Puisque les sections ne subissent qu'une rotation (et pas de déformation), on peut exprimer les déplacements en fonction de l'angle de rotation $\theta(x)$. Le déplacement $u_{1}(x,y)$ suivant x dans une section s'écrit $u_{1}=-y\theta(x)=-y\frac{du_{2}}{dx}$ ($u_{2}(x)$ est la déflexion de la ligne moyenne). Pour les contraintes, on suppose que $\sigma_{yy}=0$ ( $\varepsilon_{yy}=-\nu \varepsilon_{xx}$) et les seules contraintes significatives sont $\sigma_{xx}$ et $\tau_{xy}$ (avec $\tau_{xy}\ll\sigma_{xx}$). on a donc:

$$\sigma_{xx}=E \varepsilon_{xx}=E\frac{\partial u_{1}}{\part... ...eta}{dx}, \sigma_{xy}=\frac{E}{2(1+\nu)}\varepsilon_{xy}$$

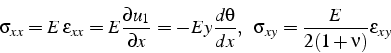
d'où l'expression du moment fléchissant $M_{z}$ en fonction de l'inertie $I$ de la section et du déplacement vertical $u_{2}$ de la ligne moyenne:

$$M_{z}=E\frac{d\theta}{dx}\int_{S}y^{2}dS=EI\frac{du_{2}^{2}}{dx^{2}}$$

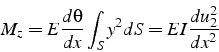
En reportant dans l'équation (2.15), on obtiens l'équation d'équilibre moyenne dans la direction $y$ (comme il n'y a pas de compression, la force axiale est nulle en moyenne dans la section $\int_{S}\sigma_{xx}ds=0$):

$$\frac{\partial^{2}}{\partial x^{2}}(EI\frac{\partial u_{2}^{2}}{\partial x^{2}})=p$$ (2.16)

C'est l'équation classique de flexion d'une poutre en statique.

En introduisant l'accélération suivant $y$, on obtiens l'équation de flexion en dynamique qui modélise les vibrations propres d'une poutre en flexion:

$$\rho S\frac{\partial^{2}u_{2}}{\partial t^{2}}=-\frac{\parti... ...}{\partial x^{2}}(EI\frac{\partial u_{2}^{2}}{\partial x^{2}})$$ (2.17)

2.2.3 Équations de bilan local en mécanique des fluides

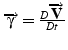En mécanique des fluides, la variable choisie pour décrire le mouvement est le champ de vitesse $\overrightarrow{\mathbf{V}}$. L'accélération d'une particule fluide de masse $dm=\rho dV$ s'écrit alors $\overrightarrow{\gamma}=\frac{D\overrightarrow{\mathbf{V}}}{Dt}$ (la dérivation $\frac{D}{Dt}$ s'effectue en suivant le mouvement de la particule). En utilisant une formulation eulérienne, dans un repère fixe lié à l'observateur, cette accélération s'écrit:

$$\overrightarrow{\gamma}=\left(\frac{\partial\overrightarrow{... ...ial y}+v_{3}\frac{\partial v_{3}}{\partial z}\end{array}\right]$$

L'équilibre d'une particule fluide (figure 2.4 ) résulte de l'équilibre entre l'accélération $\overrightarrow{\gamma}$, les contraintes $\overrightarrow{\sigma}$ exercées par l'extérieur (fluide, paroi) et les forces volumiques $\overrightarrow{f}$:

$$\rho\left[\frac{\partial\overrightarrow{\mathbf{V}}}{\partia... ...arrow{\sigma}.\overrightarrow{n} dS +\overrightarrow{f} dV$$

Figure 2.4: bilan des forces sur une particule fluide

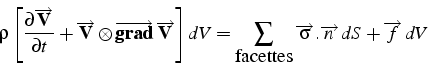
Pour un fluide le tenseur des contraintes $\overrightarrow{\sigma}$ est constitué d'une contrainte normale de pression et de contraintes visqueuses $\overrightarrow{\tau}$, proportionnelles aux gradients du champ de vitesse (fluide Newtonien).

$$\overrightarrow{\sigma}\otimes\overrightarrow{n}=-p\overrigh... ...t} \overrightarrow{\mathbf{V}}\right)\otimes\overrightarrow{n}$$

Pour un écoulement bidimensionnel (2D) on obtiens les équations d'équilibre suivantes (après passage à la limite):

$$\begin{eqnarray*} \rho\left(\frac{\partial v_{1}}{\partial t}+v_{1}\frac{\partia... ...v_{1}}{\partial y}+\frac{\partial v_{2}}{\partial x}\right)+f_{2}\end{eqnarray*}$$

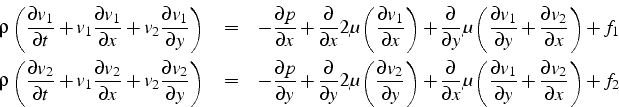
Ce sont les équations classiques de Navier-Stokes. A ce système d'équations, il faut ajouter l'équation de conservation de la masse (bilan de masse dans l'élément de volume):

$$\frac{\partial\rho}{\partial t}+div(\rho\overrightarrow{\mathbf{V}})=0$$

et dans le cas général une équation de conservation de l'énergie et une équation d'état. A partir de ces équations de Navier-Stokes on retrouve les approximations classiques:

1. fluide non visqueux ($\mu=0$)
   
   

   $$\frac{\partial\rho}{\partial t}+\frac{\partial\rho v_{1}}{\partial x}+\frac{\partial\rho v_{2}}{\partial y} = 0$$ (2.18)

   $$\frac{\partial v_{1}}{\partial t}+v_{1}\frac{\partial v_{1}}{\partial x}+v_{2}\frac{\partial v_{1}}{\partial y} = -\frac{1}{\rho}\frac{\partial p}{\partial x}$$

   $$\frac{\partial v_{2}}{\partial t}+v_{1}\frac{\partial v_{2}}{\partial x}+v_{2}\frac{\partial v_{2}}{\partial y} = -\frac{1}{\rho}\frac{\partial p}{\partial y}$$

   
   
   ce sont les équations d'Euler (avec l'équation de conservation de l'énergie et l'équation d'état)
2. écoulement non visqueux adiabatique
   dans ce cas l'équation d'énergie et l'équation d'état sont remplacées par l'équation d'adiabaticité $\frac{p}{\rho^{\gamma}}=cste$, et le système complet d'équation s'écrit:
   
   

   $$\frac{\partial\rho}{\partial t}+\frac{\partial\rho v_{1}}{\partial x}+\frac{\partial\rho v_{2}}{\partial y} = 0$$ (2.19)

   $$\frac{\partial v_{1}}{\partial t}+v_{1}\frac{\partial v_{1}}{\partial x}+v_{2}\frac{\partial v_{1}}{\partial y} = -\frac{1}{\rho}\frac{\partial p}{\partial x}$$

   $$\frac{\partial v_{2}}{\partial t}+v_{1}\frac{\partial v_{2}}{\partial x}+v_{2}\frac{\partial v_{2}}{\partial y} = -\frac{1}{\rho}\frac{\partial p}{\partial y}$$

   
   
   avec $\frac{dp}{p}=\gamma\frac{d\rho}{\rho}$. Pour un écoulement unidimensionnel, en introduisant la célérité du son $c^{2}=\gamma \frac{p}{\rho}$, on obtiens
   

   $$\frac{\partial\rho}{\partial t}+\frac{\partial\rho v_{1}}{\partial x} = 0$$ (2.20)

   $$\rho\frac{\partial v_{1}}{\partial t}+\rho v_{1}\frac{\partial v_{1}}{\partial x} = -c^{2}\frac{\partial\rho}{\partial x}$$

   
   

3. équations de l'acoustique (en 1D)
   en linéarisant le système d'équation précédant autour d'un état au repos ($\rho=\rho_{0}$, $v_{1}=0$), les fluctuations $\rho'$ et $v'_{1}$ vérifient après linéarisation:
   
   

   $$\frac{\partial\rho'}{\partial t}+\rho_{0}\frac{\partial v'_{1}}{\partial x} = 0$$ (2.21)

   $$\rho_{0}\frac{\partial v'_{1}}{\partial t}-c_{0}^{2}\frac{\partial\rho'}{\partial x} = 0$$

   
   
   qui conduisent, après élimination de $\rho'$ à l'équation classique des ondes
   
   

   $$\frac{\partial^{2}v_{1}}{\partial t^{2}}-c_{0}^{2}\frac{\partial^{2}v'_{1}}{\partial x^{2}}=0$$ (2.22)

   
   

4. fluide incompressible ( $div \overrightarrow{\mathbf{V}}=0$)
   si le fluide est incompressible ($\rho=cste$), l'équation de conservation de la masse se réduit à une contrainte sur le champ de vitesse: $div \overrightarrow{\mathbf{V}}=0$
   
   

   $$\frac{\partial v_{1}}{\partial x}+\frac{\partial v_{2}}{\partial y} = 0$$ (2.23)

   $$\frac{\partial v_{1}}{\partial t}+v_{1}\frac{\partial v_{1}}{\partial x}+v_{2}\frac{\partial v_{1}}{\partial y} = -\frac{1}{\rho}\frac{\partial p}{\partial x}+\frac{\mu}{\rho}\lef... ...rtial^{2}v_{1}}{\partial x^{2}}+\frac{\partial^{2}v_{1}}{\partial y^{2}}\right)$$

   $$\frac{\partial v_{2}}{\partial t}+v_{1}\frac{\partial v_{2}}{\partial x}+v_{2}\frac{\partial v_{2}}{\partial y} = -\frac{1}{\rho}\frac{\partial p}{\partial y}+\frac{\mu}{\rho}\lef... ...rtial^{2}v_{2}}{\partial x^{2}}+\frac{\partial^{2}v_{2}}{\partial y^{2}}\right)$$

   
   

5. fluide très visqueux en écoulement stationnaire
   dans ce cas le terme d'accélération est négligeable, et on obtiens les équations de Stockes
   
   

   $$\frac{\partial v_{1}}{\partial x}+\frac{\partial v_{2}}{\partial y} = 0$$ (2.24)

   $$-\frac{1}{\rho}\frac{\partial p}{\partial x}+\frac{\mu}{\rho}\lef... ...rtial^{2}v_{1}}{\partial x^{2}}+\frac{\partial^{2}v_{1}}{\partial y^{2}}\right) = 0$$

   $$-\frac{1}{\rho}\frac{\partial p}{\partial y}+\frac{\mu}{\rho}\lef... ...rtial^{2}v_{2}}{\partial x^{2}}+\frac{\partial^{2}v_{2}}{\partial y^{2}}\right) = 0$$

   
   

6. fluide parfait incompressible en écoulement potentiel
   les effets de viscosité sont négligés, et l'écoulement est irrotationnel à divergence nulle. Le champ de vitesse $\overrightarrow{\mathbf{V}}$ découle d'un potentiel $\Phi$: $\overrightarrow{\mathbf{V}}=\overrightarrow{grad} \Phi$, qui est solution d'une équation de Laplace:
   
   

   $$\Delta\Phi=0$$ (2.25)