TP méthode de minimisation multi-dimensionnelle

2. TP méthode de minimisation multi-dimensionnelle#

Marc Buffat Dpt mécanique, UCB Lyon 1 Minimisation 2D

%matplotlib inline
#algèbre linéaire
import numpy as np
import sympy as sp
import time
#représentation des résultats
import matplotlib.pyplot as plt
from IPython.display import display,Markdown
def printmd(text):
    display(Markdown(text))
plt.rc('font', family='serif', size='18')

from validation.validation import info_etudiant
def printmd(string):
    display(Markdown(string))
# test si numero étudiant spécifier
try: NUMERO_ETUDIANT
except NameError: NUMERO_ETUDIANT = None 
if type(NUMERO_ETUDIANT) is not int :
    printmd("**ERREUR:** numéro d'étudiant non spécifié!!!")
    NOM,PRENOM,NUMERO_ETUDIANT=info_etudiant()
    #raise AssertionError("NUMERO_ETUDIANT non défini")
# parametres spécifiques
_uid_    = NUMERO_ETUDIANT
np.random.seed(_uid_)
printmd("**Login étudiant {} {} uid={}**".format(NOM,PRENOM,_uid_))
# fonctionnelle a minimiser
import pwd,sys
libpath=pwd.getpwnam('cours')[5]+'/IntroIA/lib'
sys.path.insert(0, libpath)
from Fonctionnelle import Fonctionnelle
J = Fonctionnelle(_uid_)
printmd("**Fonctionnelle J à minimiser**")
J.info()

ERREUR: numéro d’étudiant non spécifié!!!

Login étudiant Marc BUFFAT uid=137764122

Fonctionnelle J à minimiser

Fonctionnelle J(X) 
dimension de X : 43
minimum   de J : -1.7692176662626187
pour ||X|| < 1.0

2.1. Objectifs#

Trouver le vecteur X minimisant la fonction J(X).

Cette fonction J() est implémentée en Python comme un objet (instance de classe):

  • J : nom de l’objet

  • J.dim() : dimension de X, i.e. le nombre de variables dont J dépend

  • J(X) : calcul la valeur de J pour un vecteur X de dimension J.dim()

  • J.grad(X) : calcul le gradient de J en X

  • J.err(X) : calcul la norme de l’erreur ||X-Xe|| où Xe minimise J(X)

  • J.min() : calcul le minimum de J

2.2. Minimisation 1D#

Etude de la minimisation de \(J(\mathbf{X})\) dans une direction \(\mathbf{D}\) fixée

On choisit un vecteur \(D\) (imposé), et on cherche à minimiser \(J(\alpha \mathbf{D})\)

Dans les cellules suivantes:

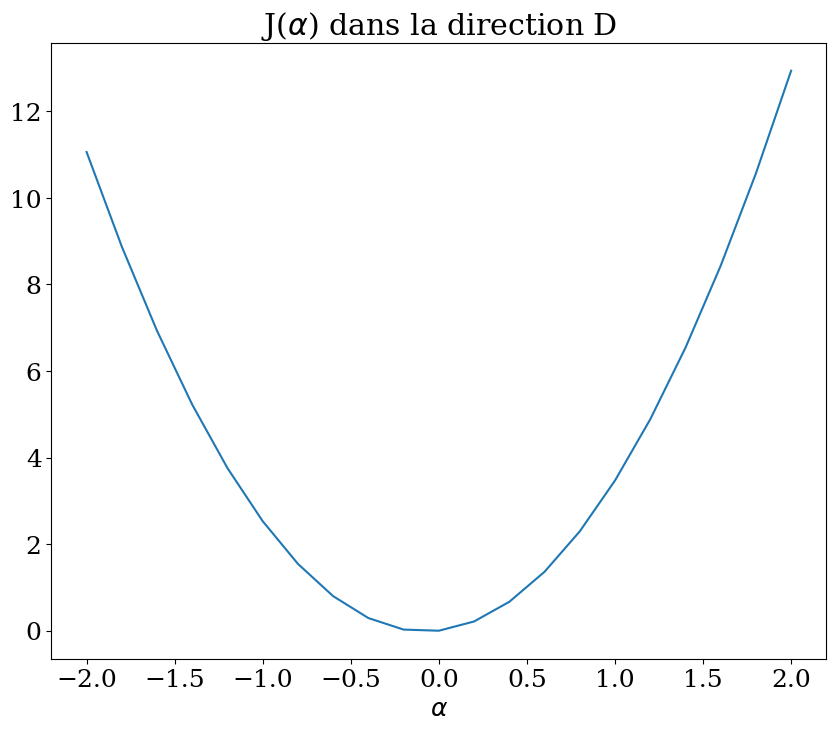
  • calculer \(J(\alpha \mathbf{D})\) pour des valeurs de \(\alpha\) entre -2 et 2

  • tracer la fonction \(J(\alpha)\)

  • utiliser la fonction minimize_scalar de scipy pour calculer le mimimum en \(\alpha\)

  • mettre le resultat dans la variable alpha_min

# calcul variation dans une direction D
D = np.zeros(J.dim())
D[NUMERO_ETUDIANT % J.dim()] = 1
Alpha = None
JAlpha = None

### BEGIN SOLUTION
Alpha  = np.linspace(-2,2,21)
JAlpha = np.array([J(alpha*D) for alpha in Alpha])
plt.figure(figsize=(10,8))
plt.plot(Alpha,JAlpha)
plt.xlabel("$\\alpha$")
plt.title("J($\\alpha$) dans la direction D");
### END SOLUTION
../../../_images/40d47e1545600b36fe7c8c9a1eb737f7e21e82588e7a6a3c393329eae262a68e.png 
from scipy.optimize import minimize_scalar

alpha_min = None
### BEGIN SOLUTION
F = lambda al
pha:J(alpha*D)
res = minimize_scalar(F,method='Brent')
print("Jmin=",res.fun)
alpha_min = res.x
print("solution alpha=",alpha_min)
X = alpha_min*D
print("err=",J.err(X))
res
### END SOLUTION

  Cell In[4], line 5
    F = lambda al
                 ^
SyntaxError: invalid syntax

print(f"alpha={alpha_min} minimise J suivant D\n",D)
assert(J.err1D(alpha_min,D)<1.e-5)

2.3. Minimisation multi-dimensionelle#

utilisation de la bibliothéque scipy

  • fonction minimize (minimisation locale)

    • méthode de gradients exactes: Gradients Conjugués, Newton GC,

    • méthode de gradients approchées: BFGS,

    • line search Powell, Simplex Nelder-Mead

  • optimisation globale

    • simulated annealing

Dans la cellule suivante, définir 2 nouvelles fonctions

  • F(X) qui calcul J(X)

  • Fgrad(X) qui calcule le gradient

on définit des fonctions python car les méthodes de minimisation n’autorisent pas les méthodes de classe

F = None
Fgrad = None
### BEGIN SOLUTION
F = lambda X:J(X)
Fgrad = lambda X:J.grad(X)
### END SOLUTION
X0 = np.zeros(J.dim())

print("solution initiale X0:\n",X0)
assert np.allclose(F(X0),J(X0))
assert np.allclose(Fgrad(X0),J.grad(X0))

2.3.1. Méthode par défaut#

pour chacune des méthodes:

  • on calcule la solution obtenue Xe,

  • la valeur de J

  • l’erreur (qui doit etre inférieure à 1.e-5)

Il faut aussi jouer sur les paramètres optionnels de la fonction

from scipy.optimize import minimize

Xe = None
### BEGIN SOLUTION




res = minimize(F, X0,options={'disp':True})
Xe = res.x
print("Jmin=",res.fun,res.message)
print('solution J(Xe)={J(Xe)} pour Xe:\n',Xe)
print("Erreur = ",J.err(Xe))
### END SOLUTION

print(f"J={J(Xe)} avec erreur={J.err(Xe)} pour  X:\n",Xe)
assert( J.err(Xe) < 1.e-5)

2.3.2. Méthode de gradient conjugué#

Xe = None
### BEGIN SOLUTION
res = minimize(F, X0, jac=Fgrad, method='CG',options={'disp':True})
print("Jmin=",res.fun,res.message)
Xe = res.x
print('solution J(Xe)={J(Xe)} pour Xe:\n',Xe)
print("Erreur = ",J.err(Xe))
### END SOLUTION

print(f"J={J(Xe)} avec erreur={J.err(Xe)} pour  X:\n",Xe)
assert( J.err(Xe) < 1.e-5)

2.3.3. Méthode de gradient conjugué avec Newton#

Xe = None
### BEGIN SOLUTION
res = minimize(F, X0, jac=Fgrad, method='Newton-CG',options={'disp':True})
print("Jmin=",res.fun,res.message)
Xe = res.x
print('solution J(Xe)={J(Xe)} pour Xe:\n',Xe)
print("Erreur = ",J.err(Xe))
### END SOLUTION

print(f"J={J(Xe)} avec erreur={J.err(Xe)} pour  X:\n",Xe)
assert( J.err(Xe) < 1.e-5)

2.3.4. Méthode BFGS (gradient avec calcul d’un gradient numérique)#

Xe = None
### BEGIN SOLUTION
res = minimize(F, X0, method='BFGS',options={'disp':True})
print("Jmin=",res.fun,res.message)
Xe = res.x
print('solution J(Xe)={J(Xe)} pour Xe:\n',Xe)
print("Erreur = ",J.err(Xe))
### END SOLUTION

print(f"J={J(Xe)} avec erreur={J.err(Xe)} pour  X:\n",Xe)
assert( J.err(Xe) < 1.e-5)

2.3.5. Algorithme Powell (line search 2D)#

Xe = None
### BEGIN SOLUTION
res = minimize(F, X0, method='Powell',options={'disp':True,'xtol':1.e-8,'ftol':1.0e-8})
print("Jmin=",res.fun,res.message)
Xe = res.x
print('solution J(Xe)={J(Xe)} pour Xe:\n',Xe)
print("Erreur = ",J.err(Xe))
### END SOLUTION

print(f"J={J(Xe)} avec erreur={J.err(Xe)} pour  X:\n",Xe)
assert( J.err(Xe) < 1.e-3)

2.3.6. Simulated annealing#

from scipy.optimize import dual_annealing

Xe = None
### BEGIN SOLUTION
bounds = [[-1,1]]*J.dim()
res=dual_annealing(F,bounds=bounds)
print(res)
print("Jmin=",res.fun,res.message)
Xe = res.x
print('solution J(Xe)={J(Xe)} pour Xe:\n',Xe)
print("Erreur = ",J.err(Xe))
### END SOLUTION

print(f"J={J(Xe)} avec erreur={J.err(Xe)} pour  X:\n",Xe)
assert( J.err(Xe) < 1.e-4)

2.3.7. Méthode du Simplex (Nelder-Mead)#

Xe = None
### BEGIN SOLUTION
bounds = [[-1,1]]*J.dim()
res = minimize(F, X0, method='Nelder-Mead',bounds=bounds,
               options={'disp':True, 'maxiter':500000, 'ftol':1.0e-9,'xtol':1.0e-9})
print("Jmin=",res.fun,res.message)
Xe = res.x
print('solution J(Xe)={J(Xe)} pour Xe:\n',Xe)
print("Erreur = ",J.err(Xe))
# non cvge
### END SOLUTION

print(f"J={J(Xe)} avec erreur={J.err(Xe)} pour  X:\n",Xe)
#assert( J.err(Xe) < 0.8)

2.4. Analyse#

comparaison des méthodes

  • coût

  • précision

Ecrivez votre analyse en markdown

2.5. FIN#

Contents