suivant: 2. Construction de schéma monter: 1. Une première approche précédent: 1.5 Étude de la Table des matières
Pour valider les analyses précédentes, nous allons utiliser Matlab
pour simuler les problèmes
![]() et
et
![]() .
.
La fonction Matlab expliciteP1, donnée dans le programme
1.6.1, calcule l'erreur
![]() au temps
au temps
![]() entre la solution exacte
entre la solution exacte
![]() et la solution numérique
et la solution numérique
![]() calculée avec
calculée avec
![]() intervalles, un paramètre
intervalles, un paramètre
![]() fixé,
et pour une condition initiale modale:
fixé,
et pour une condition initiale modale:
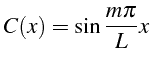
La programmation Matlab est très simple. Avec Matlab, les vecteurs
ont un indice qui commence à 1. La solution est donc stockée dans
un vecteur
![]() de dimension
de dimension
![]() . On effectue
une boucle en temps (ligne 16 à 20), pour calculer la solution
. On effectue
une boucle en temps (ligne 16 à 20), pour calculer la solution
![]() .
En utilisant les notations matricielles de Matlab, la solution aux
noeuds internes
.
En utilisant les notations matricielles de Matlab, la solution aux
noeuds internes
![]() s'écrit (ligne 18):
s'écrit (ligne 18):
Dans cette expression, à droite du signe =,
![]() représente le vecteur
solution connu à l'instant
représente le vecteur
solution connu à l'instant
![]() . La nouvelle valeur de
. La nouvelle valeur de
![]() ( à
gauche du signe =) représente la nouvelle solution calculée à l'instant
( à
gauche du signe =) représente la nouvelle solution calculée à l'instant
![]() .
.
function [ErrMax,U]=expliciteP1(N,r,t0,m)
% schema explicite pble P1
% calcul la solution U et l'erreur ErrMax
% a t=t0 sur N points
% pour une valeur du parametre r fixe
% pour une condition initiale sin(m*Pi*X)
% parametres
L=1;
h=1.0/N; dt=r*h^2; Ndt=round(t0/dt)
% liste des nds internes et pts du maillage
Ni=[2:N];
X=[0:h:L];
% condition initiale C
C=sin(m*pi*X);
t=0; U=C;
for it=1:Ndt
t=t+dt;
U(Ni)=(1-2*r)*U(Ni)+r*(U(Ni-1)+U(Ni+1));
U(1)=0; U(N+1)=0;
end;
% calcul de l'erreur
Ue=C*exp(-m^2*pi^2*t);
ErrMax=norm(Ue-U,inf);
englishANIMATION:Calcul de la solution numérique explicite du problème (
![]() )
)
On a tout d'abord tracé la solution numérique calculée à un instant
![]() pour
pour
![]() ,
,
![]() ,
,
![]() et deux valeurs de
et deux valeurs de
![]() (figure 1.6).
(figure 1.6).
Pour
![]() (figure 1.6a), la solution numérique
décroit comme la solution exacte, i.e. l'amplitude de la solution
numérique décroit de
(figure 1.6a), la solution numérique
décroit comme la solution exacte, i.e. l'amplitude de la solution
numérique décroit de
![]() , alors que la solution exacte décroit
de
, alors que la solution exacte décroit
de
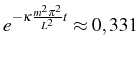 .
.
Par contre pour
![]() (figure 1.6b), la solution numérique
diverge avec une apparition d'oscillations à hautes fréquences d'amplitudes
croissantes, comme prévue dans la thèorie.
(figure 1.6b), la solution numérique
diverge avec une apparition d'oscillations à hautes fréquences d'amplitudes
croissantes, comme prévue dans la thèorie.
Pour les mêmes paramêtres , on a ensuite tracé sur la figure (1.7)
l'évolution temporelle de la valeur maximale de la solution numérique
calculée pour différentes valeurs du pas en temps
![]() et pour deux
maillages
et pour deux
maillages
![]() et
et
![]() . On les a comparé à la valeur de exacte
déduite de (1.18):
. On les a comparé à la valeur de exacte
déduite de (1.18):
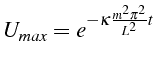
Pour
![]() , on constate que la solution numérique et la solution
exacte sont très proches tant que
, on constate que la solution numérique et la solution
exacte sont très proches tant que
![]() , et que la solution
numérique diverge pour
, et que la solution
numérique diverge pour
![]() . De même pour
. De même pour
![]() , la
solution numérique converge tant que
, la
solution numérique converge tant que
![]() et diverge
sinon. Ces valeurs du pas en temps correspondent justement à la valeur
limite de stabilité du paramêtre
et diverge
sinon. Ces valeurs du pas en temps correspondent justement à la valeur
limite de stabilité du paramêtre
![]() (1.36):
(1.36):
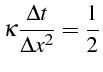
De façon à analyser la précision de la solution numérique, on a tracé
sur la figure (1.8) pour
![]() et
et
![]() ,
l'évolution de l'erreur
,
l'évolution de l'erreur
![]() pour des valeurs
de
pour des valeurs
de
![]() de 8 à 256, et différentes valeurs de
de 8 à 256, et différentes valeurs de
![]() .
.
On vérifie sur cette figure (1.8) la décroissance quadratique
de l'erreur, à
![]() fixé, en fonction de
fixé, en fonction de
![]() , puisque l'erreur théorique
est en
, puisque l'erreur théorique
est en
![]() . A
. A
![]() fixé, lorsque l'on divise
fixé, lorsque l'on divise
![]() par 2, on divise
par 2, on divise
![]() par 4 et l'erreur est divisée
d'un facteur 4. On note aussi que pour
par 4 et l'erreur est divisée
d'un facteur 4. On note aussi que pour
![]() , la convergence
est plus rapide car la valeur du pas en temps
, la convergence
est plus rapide car la valeur du pas en temps
![]() correspond
au cas particulier c1eq28b pour lequel le premier terme de
l'erreur de troncature est nul. L'erreur de troncature est dans ce
cas en
correspond
au cas particulier c1eq28b pour lequel le premier terme de
l'erreur de troncature est nul. L'erreur de troncature est dans ce
cas en
![]() et l'erreur décroit en
et l'erreur décroit en
![]() .
.
On constate enfin que pour
![]() , le schéma diverge, mais uniquement
pour les grandes valeurs de
, le schéma diverge, mais uniquement
pour les grandes valeurs de
![]() . En effet pour
. En effet pour
![]() grand, on effectue
beaucoup plus d'itérations que pour
grand, on effectue
beaucoup plus d'itérations que pour
![]() petit et les erreurs d'arrondis
sont suffisament amplifiées pour faire diverger la solution.
petit et les erreurs d'arrondis
sont suffisament amplifiées pour faire diverger la solution.
On note enfin que l'erreur diminue à
![]() fixé avec
fixé avec
![]() , c'est à
dire avec
, c'est à
dire avec
![]() (avec un cas particulier pour
(avec un cas particulier pour
![]() ).
).
La discrétisation explicite du problème
![]() conduit à la même
équation aux différences (1.35), que pour le problème
conduit à la même
équation aux différences (1.35), que pour le problème
![]() .
La seule différence provient de la condition aux limites en
.
La seule différence provient de la condition aux limites en
![]() .
Pour le problème
.
Pour le problème
![]() , la condition aux limites est une condition
de symétrie:
, la condition aux limites est une condition
de symétrie:
![]() , que l'on doit discrétiser
pour obtenir la valeur numérique
, que l'on doit discrétiser
pour obtenir la valeur numérique
![]() au premier point du
maillage. Nous étudierons deux façons d'imposer cette condition aux
limites de type Neumann:
au premier point du
maillage. Nous étudierons deux façons d'imposer cette condition aux
limites de type Neumann:
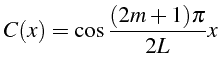
ou une condition initiale d'Heaviside si
![]() (dont on a calculé
une solution exacte au paragraphe c1par1):
(dont on a calculé
une solution exacte au paragraphe c1par1):
function [ErrMax,U]=expliciteP2(N,r,t0,m)
% schema explicite pble P2
% calcul la solution U et l'erreur ErrMax
% a t=t0 sur N points
% pour une valeur du parametre r fixe
% pour une condition initiale cos((m+1)*Pi/2*X) si m>=0
% ou fonction porte si m<0
% parametres
L=1;
h=1.0/N; dt=r*h^2; Ndt=round(t0/dt)
% liste des nds internes et pts du maillage
Ni=[2:N];
X=[0:h:L];
% condition initiale C
if (m>=0)
C=cos((2*m+1)*pi/2*X);
else
% coefficient de Fourier
delta=1/10;
M=[0:20];
CM=4*(sin(pi*M*delta)*cos(pi*delta/2)+...
cos(pi*M*delta)*sin(pi*delta/2))./((2*M+1)*pi);
C=CM*cos(pi/2*(2*M+1)'*X);
end;
t=0; U=C;
for it=1:Ndt
t=t+dt;
Un=U;
U(Ni)=(1-2*r)*Un(Ni)+r*(Un(Ni-1)+Un(Ni+1));
% conditions aux limites
U(1)=(1-2*r)*Un(1)+r*2*Un(2);
U(N+1)=0;
end;
% calcul de l'erreur
if (m>=0)
Ue=C*exp(-((2*m+1)*pi/2)^2*t);
else
Ue=(CM.*exp(-(2*M+1).^2*pi^2/4*t))*cos(pi/2*(2*M+1)'*X);
end;
ErrMax=norm(Ue-U,inf);
La programmation Matlab est identique à celle du programme (1.6.1).
On notera simplement l'utilisation de la notation matricielle pour
le calcul de la solution analytique Ue (équation 1.20)
aux noeuds du maillage (ligne 21 et 38) sur
![]() modes à l'instant
modes à l'instant
![]() :
:
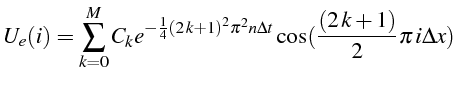
où les
![]() sont données par l'équation 1.21:
sont données par l'équation 1.21:
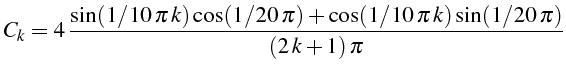
En notant
![]() les modes utilisés pour la calcul de la solution,
le tableau
les modes utilisés pour la calcul de la solution,
le tableau
![]() des coefficients
des coefficients
![]() est calculé directement
à la ligne 21. Le vecteur solution exacte
est calculé directement
à la ligne 21. Le vecteur solution exacte
![]() aux noeuds du maillage
est calculé à la ligne 38 en multipliant terme à terme le vecteur
aux noeuds du maillage
est calculé à la ligne 38 en multipliant terme à terme le vecteur
![]() par le vecteur
par le vecteur
![\bgroup\color{black}$ \left[e^{-1/4 \left(2 M+1\right)^{2}\pi^{2}t}\right]$\egroup](img571.png) (opérateur
(opérateur
![]() ), puis en effectuant le produit scalaire (opérateur
), puis en effectuant le produit scalaire (opérateur
![]() ) avec le vecteur colonne
) avec le vecteur colonne
![]() pour effectuer la somme.
pour effectuer la somme.
La boucle en temps correspond aux lignes 26 à 33 , et la condition
aux limites en
![]() est imposée à la ligne 31 (condition miroir
1.55 dans le programme 1.6.2). Pour l'autre condition
(1.53), il suffit de remplacer la ligne 31 par:
est imposée à la ligne 31 (condition miroir
1.55 dans le programme 1.6.2). Pour l'autre condition
(1.53), il suffit de remplacer la ligne 31 par:
On a tracé sur la figure (1.9) la solution calculée pour
![]() et
et
![]() à différents instants (
à différents instants (
![]() est le temps
caractéristique de diffusion
est le temps
caractéristique de diffusion
![]() ).
En comparant avec la solution exacte de la figure (1.2b),
on constate que les solutions sont très proches.
).
En comparant avec la solution exacte de la figure (1.2b),
on constate que les solutions sont très proches.
Pour le vérifier, on a tracé sur la figure (1.10) l'évolution
de l'erreur entre la solution exacte (calculée avec 20 modes) et la
solution numérique à
![]() pour des valeurs de
pour des valeurs de
![]() de 20 à 640, différentes valeurs de
de 20 à 640, différentes valeurs de
![]() et les deux types de prise
en compte de la condition aux limites en
et les deux types de prise
en compte de la condition aux limites en
![]() . Avec la condition
miroir (1.55), on constate que l'erreur, à
. Avec la condition
miroir (1.55), on constate que l'erreur, à
![]() fixé, décroit
de façon quadratique en
fixé, décroit
de façon quadratique en
![]() , ce que prévoit bien la théorie
du schéma explicite avec une précision en
, ce que prévoit bien la théorie
du schéma explicite avec une précision en
![]() .
Par contre si on impose la condition (1.53), l'erreur décroit
linéairement en
.
Par contre si on impose la condition (1.53), l'erreur décroit
linéairement en
![]() .
.
On constate ici un point important sur la précision des schémas numériques.
La précision d'un schéma numérique dépend à la fois de la précision du schéma interne et de la précision de la discrétisation des conditions aux limites.
Avec la condition (1.53), on calcule la valeur
![]() avec
une approximation d'ordre
avec
une approximation d'ordre
![]() (discrétisation décentrée),
alors que avec la condition (1.55), la valeur de
(discrétisation décentrée),
alors que avec la condition (1.55), la valeur de
![]() est calculée à l'ordre
est calculée à l'ordre
![]() (discrétisation centrée),
et on conserve une approximation en
(discrétisation centrée),
et on conserve une approximation en
![]() pour
pour
![]() .
Donc avec une condition au limite d'ordre 1 en
.
Donc avec une condition au limite d'ordre 1 en
![]() , même
avec un schéma interne d'ordre 2 en
, même
avec un schéma interne d'ordre 2 en
![]() , la solution
a une précision d'ordre 1 en
, la solution
a une précision d'ordre 1 en
![]() .
.
Pour terminer cette analyse, nous avons calculé la solution numérique
avec
![]() et
et
![]() pour une condition initiale
pour une condition initiale
![]() .
Le résultat est tracé sur la figure (1.11). On constate
sur cette figure l'apparition d'oscillations numériques dès les premières
itérations en temps, qui sont ensuite amorties au cours du temps.
Ces oscillations numériques n'apparaisent que pour des valeurs de
.
Le résultat est tracé sur la figure (1.11). On constate
sur cette figure l'apparition d'oscillations numériques dès les premières
itérations en temps, qui sont ensuite amorties au cours du temps.
Ces oscillations numériques n'apparaisent que pour des valeurs de
![]() comprises entre
comprises entre
![]() et
et
![]() , et uniquement
si la condition initiale possède des modes hautes fréquences. C'est
ce que prévoit l'analyse théorique du paragraphe c1convge.
, et uniquement
si la condition initiale possède des modes hautes fréquences. C'est
ce que prévoit l'analyse théorique du paragraphe c1convge.
englishANIMATION:Calcul de la solution numérique explicite du problème (
![]() )
)