suivant: 1.3 Recherche de solution monter: 1. Une première approche précédent: 1.1 Introduction Table des matières
![\includegraphics[clip,width=0.8\textwidth]{CHAP1/barre1}](img164.png)
Considérons le problème de la diffusion de la chaleur dans une barre
homogène, de coefficient de conduction
![]() , de masse volumique
, de masse volumique
![]() , de coefficient calorifique
, de coefficient calorifique
![]() , de section
, de section
![]() et de
longueur
et de
longueur
![]() , sans production d'énergie interne
, sans production d'énergie interne
![]() En supposant
que les deux extrémités sont maintenues à une température constante
En supposant
que les deux extrémités sont maintenues à une température constante
![]() , l'équation de conservation de l'énergie s'écrit:
, l'équation de conservation de l'énergie s'écrit:
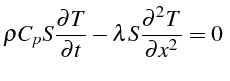 pour
pour
auquel on associe deux conditions aux limites
![]() ,
,
![]() et une condition initiale
et une condition initiale
![]() .
.
En effectuant le changement de variable
![]() , on obtient le
problème modèle
, on obtient le
problème modèle
![]() suivant avec des conditions
aux limites de type Dirichlet homogènes (c'est à
dire que la valeur de
suivant avec des conditions
aux limites de type Dirichlet homogènes (c'est à
dire que la valeur de
![]() est imposée égale à zéro aux extrémités
est imposée égale à zéro aux extrémités
![]() et
et
![]() ):
):
|
|
Dans cette équation
![]() est la diffusivité
thermique du matériau,
est la diffusivité
thermique du matériau,
![]() la température relative, et
la température relative, et
![]() la répartition de température relative initiale
la répartition de température relative initiale
![]() .
.
Dans le but d'obtenir une solution de référence pour les simulations
numériques, nous allons chercher une solution analytique du problème
![]() , en utilisant la méthode classique de séparation de variables.
, en utilisant la méthode classique de séparation de variables.
Pour résoudre
![]() , on considère le problème sans condition
initiale fixée:
, on considère le problème sans condition
initiale fixée:
On cherche une solution élémentaire de ce problème
![]() sous la forme à variables séparées:
sous la forme à variables séparées:
En divisant par
![]() , il vient:
, il vient:
L'examen de l'équation (1.5) montre que le membre de gauche
est une fonction de
![]() seulement, tandis que le membre de droite
n'est fonction que de
seulement, tandis que le membre de droite
n'est fonction que de
![]() Par conséquent si
Par conséquent si
![]() varie et
varie et
![]() reste
constant,
reste
constant,
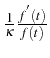 reste constant.
De même, si
reste constant.
De même, si
![]() varie et
varie et
![]() reste constant
reste constant
![]() reste aussi constant. Chacun de ces membres doit donc être constant,
disons égale à
reste aussi constant. Chacun de ces membres doit donc être constant,
disons égale à
![]() D'où les 2 équations:
D'où les 2 équations:
que l'on réécrit sous la forme:
En intégrant l'équation pour
![]() (1.8), il vient:
(1.8), il vient:
Le signe de la constante
![]() donne l'évolution de la température
au cours du temps (puisque
donne l'évolution de la température
au cours du temps (puisque
![]() ). Si la constante
). Si la constante
![]() est positive, la température croit exponentiellement, ce qui n'est
physiquement pas acceptable. Par contre si la constante
est positive, la température croit exponentiellement, ce qui n'est
physiquement pas acceptable. Par contre si la constante
![]() est
négative, la température décroît exponentiellement, ce qui est à priori
la solution à retenir. Nous envisagerons cependant les 2 cas, et nous
montrerons que seul le second cas conduit à une solution non identiquement
nulle.
est
négative, la température décroît exponentiellement, ce qui est à priori
la solution à retenir. Nous envisagerons cependant les 2 cas, et nous
montrerons que seul le second cas conduit à une solution non identiquement
nulle.
En supposant
![]() on pose
on pose
![]() (
(
![]() est une constante arbitraire). En réécrivant l'équation pour
est une constante arbitraire). En réécrivant l'équation pour
![]() (1.9), on obtient :
(1.9), on obtient :
Cette équation (1.11) est une équation du second ordre homogène
et à coefficients constants. Cherchons la solution sous la forme :
![]() . On obtient alors l'équation caractéristique :
. On obtient alors l'équation caractéristique :
![]() qui fixe les valeurs possibles de
qui fixe les valeurs possibles de
![]() , d'où la solution
, d'où la solution
![]() :
:
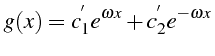
ou encore :
La solution
![]() de (1.2) de s'écrit alors
:
de (1.2) de s'écrit alors
:
![\bgroup\color{black}$\displaystyle u(x,t)=e^{(\kappa\omega^{2}t)}\left[A ch(\omega x)+B sh(\omega x)\right]$\egroup](img217.png)
avec
![]()
![]() et
et
![]() des constantes. On peut montrer
sans difficulté que l'application des conditions aux limites du problème
des constantes. On peut montrer
sans difficulté que l'application des conditions aux limites du problème
![]() conduit à
conduit à
![]() et donc à une solution identiquement
nulle.
et donc à une solution identiquement
nulle.
En supposant maintenant
![]() , on pose
, on pose
![]() , et dans ce cas en suivant la même démarche que précédemment, on
montre que la solution s'écrit :
, et dans ce cas en suivant la même démarche que précédemment, on
montre que la solution s'écrit :
![\bgroup\color{black}$\displaystyle u(x,t)=e^{-(\kappa\omega^{2}t)}\left[A \cos(\omega x)+B \sin(\omega x)\right]$\egroup](img224.png)
L'application de la première condition aux limites
![]() en
en
![]() donne :
donne :
![\bgroup\color{black}$\displaystyle e^{-(\kappa\omega^{2}t)}\left[A+0\right]=0\Rightarrow A=0$\egroup](img226.png)
![]() s'écrit alors:
s'écrit alors:
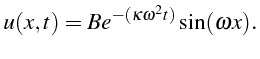
L'application de la deuxième condition en
![]() implique
:
implique
:
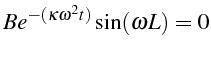
Si on choisit
![]() on retrouve une solution identiquement nulle.
On suppose donc que
on retrouve une solution identiquement nulle.
On suppose donc que
![]() et nous obtenons puisque
et nous obtenons puisque
![]()
![]() :
:
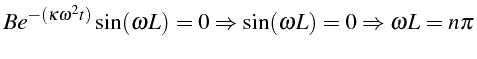
Cette condition fixe les valeurs possibles de
![]() :
:
![]() (
(
![]()
La solution de
![]() s'écrit:
s'écrit:
où les
![]() sont des constantes arbitraires. On constate que puisque
l'on a fixé aucune condition initiale, le problème
sont des constantes arbitraires. On constate que puisque
l'on a fixé aucune condition initiale, le problème
![]() admet une infinité de solutions.
admet une infinité de solutions.
Les solutions (1.14) satisfont l'équation et les
conditions aux limites du problème
![]() . Pour satisfaire la
condition initiale (
. Pour satisfaire la
condition initiale (
![]() ), nous devons avoir :
), nous devons avoir :
Le problème revient maintenant à la détermination des
![]() de
sorte que la série (1.15) converge vers
de
sorte que la série (1.15) converge vers
![]() pour tout
pour tout
![]() . Pour calculer les constantes
. Pour calculer les constantes
![]() , on multiplie
l'équation (1.15) par
, on multiplie
l'équation (1.15) par
![]() , et on intégre
sur l'intervalle
, et on intégre
sur l'intervalle
![]() . En utilisant l'orthogonalité des fonctions
sinus:
. En utilisant l'orthogonalité des fonctions
sinus:
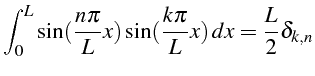
on obtiens la valeur de
![]()
Les
![]() sont les coefficients de Fourier de la fonction périodique
de période
sont les coefficients de Fourier de la fonction périodique
de période
![]() coïncidant avec
coïncidant avec
![]() sur l'intervalle
sur l'intervalle
![]() .
.
|
La solution générale du problème
|
Dans le cas particulier
![]() , on trouve le
mode propre (i.e. une solution qui évolue de façon auto-similaire
au cours du temps) d'ordre
, on trouve le
mode propre (i.e. une solution qui évolue de façon auto-similaire
au cours du temps) d'ordre
![]() du problème
du problème
![]() :
:
Ce mode propre décroît de façon auto-similaire et exponentiellement
au cours du temps proportionnellement au carré de sa longueur d'onde
![]() .
.
Cela montre qu'une fluctuation de température est d'autant plus
amortie au cours du temps que sa longueur d'onde
![]() est courte. C'est un phénomène caractéristique des processus de diffusion.
est courte. C'est un phénomène caractéristique des processus de diffusion.