1.3 Recherche de solution analytique avec Maple

Nous allons appliquer la démarche précédente pour calculer la solution analytique d'un autre problème de conduction en utilisant Maple pour effectuer les calculs analytiques. Le problème étudié $(P_{2})$ différe du problème $(P_{1})$ précédent par les conditions aux limites et la condition initiale.

1.3.1 Problème physique: conduction dans une barre

On considère l'évolution de la température $T(x,t)$ dans un barreau de coefficient de conduction $\lambda,$ de section $S$ , de longueur $2L$ , maintenu à une température constante $T_{0}$ sur chacune de ses extrémités, et chauffé initialement en son milieu à une température $T_{1}$ sur une longueur de $2l=\frac{2L}{10}$ .

L'équation d'équilibre s'écrit:

$$\rho C_{p}S\frac{\partial T}{\partial t}-\lambda S\frac{\partial^{2}T}{\partial x^{2}}=0$$

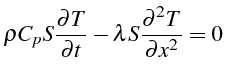
avec les conditions aux limites:

$$T(L,t)=T_{0}$$   et  $$T(-L,t)=T_{0}$$

et la condition initiale:

$$T(x,0)=T_{i}(x)$$

$T_{i}(x)$ est la répartition de température à l'instant initial, supposée symétrique par rapport à $x=0$ .

1.3.2 Problème modèle

En posant $u=\frac{T-T_{0}}{T_{1}-T_{0}}$ , $x=\frac{X}{L}$ , $\kappa=\frac{\lambda}{\rho C_{p}}$ , $\delta=\frac{l}{L}$ et en tenant compte de la symétrie par rapport à $x=0$ , le problème modèle $(P_{2})$ s'écrit:

$$(P_{2})\left\{ \begin{array}{l} \frac{\partial u}{\partial t}=\ka... ...u}{\partial x}\right)_{x=0}=0, u(t,x=1)=0 u(x,t=0)=C(x)\end{array}\right.$$ (1.19)

1.3.3 Recherche de solutions analytiques

On utilise Maple pour calculer la solution dans deux cas:

1. cas 1: condition initiale gaussienne
2. cas 2: condition initiale créneau

englishANIMATION:Méthode de séparation de variables pour l'équation de la chaleur

Le programme Maple (1.3.3) calcule la solution générale de (1.19) en utilisant la méthode de séparation de variables décrite précédemment.

programme Maple 1.3.3: Méthode de séparation de variables pour l'équation de la chaleur 1.19

# Methode de separation de variables: equation de la chaleur
# Cas général
> restart:with(plots):
# equation et conditions aux limites
> diff(u(t,x),t)-K*diff(u(t,x),x$2)=0; EQ:=%:
> D[2](u)(t,0); u(t,1)=0; CL:={%%,%}:
# recherche solution exacte
> u(t,x)=A(t)*B(x);rel1:=%:
> expand(simplify(subs(rel1,EQ/(K*u(t,x))))):
> P:=[op(lhs(%))]:P[1]=-P[2];
# determination de la solution elementaire en x
> Be:=unapply(rhs(dsolve({P[2]=omega^2},B(x))),x);
# prise en compte des conditions aux limites
> D(Be)(0)=0;Be(1)=0;
> -C1=0; omega=(2*k+1)*Pi/2;
> Be:=(x,k)->cos((2*k+1)*Pi/2*x);
# détermination de la solution en t
> Ae:=rhs(dsolve({P[1]=-((2*k+1)*Pi/2)^2},A(t)));
> Ae:=(t,k)->exp(-((2*k+1)*Pi/2)^2*K*t);
# solution générale
> Ug:=unapply(sum(C[k]*Ae(t,k)*Be(x,k),k=0..N),t,x);
# prise en compte de la C.I. a t=0
> Ug(0,x)=C(x);
# vérification de l'orthogonalite des fonctions élémentaires
# pour le calcul des coefficients
> assume(i,integer);assume(k,integer);
> int(cos((2*k+1)*Pi/2*x)*cos((2*i+1)*Pi/2*x),x=0..1);
> int(cos((2*k+1)*Pi/2*x)*cos((2*k+1)*Pi/2*x),x=0..1);
# détermination des coefficients de Fourier
> k:='k':
> C[k]=2*int(C(x)*cos((2*k+1)*Pi/2*x),x=0..1); rel2:=%:
# Expression de la solution générale Ug
> N:='N':
> Ug:=unapply(subs(rel2,Ug(t,x)),t,x);

Dans le programme (1.3.3), on cherche une solution élémentaire $u(x,t)=A(t)*B(x)$ (ligne 8) de l'équation notée $EQ$ (ligne 5). On substitue cette solution dans l'équation $EQ$ (ligne 9), et on en déduit les 2 équations en $A(t)$ et en $B(x)$ (ligne 10), que l'on stocke dans le tableau $P$ . On détermine ensuite la solution générale de l'équation différentielle sur $B(x)$ (ligne 12), et on impose les conditions aux limites (lignes 14 et 15), ce qui fournit la solution $B_{e}$ qui dépend de $x$ et d'un paramètre entier $k$ (ligne 16):

$$B_{e}:=((x,k)\mapsto\cos(1/2 \left(2 k+1\right)\pi x))$$

De même la solution pour $A(t)$ est calculée à la ligne 18. Cette solution $A_{e}$ dépend de $t$ et du paramètre entier $k$ (ligne 19).

$$A_{e}:=(t,k)\mapsto e^{-1/4 \left(2 k+1\right)^{2}\pi^{2}Kt}$$

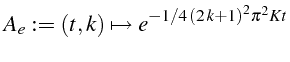
La solution générale $U_{g}$ de l'équation est donc une somme à priori infinie (i.e. $N=\infty$ ) de ces solutions élémentaires (ou modes propres)

$$U_{g}:=({t,x})\mapsto\sum_{k=0}^{N}C_{{k}}{e^{-1/4 \left(2 k+1\right)^{2}\pi^{2}Kt}}\cos(1/2 \left(2 k+1\right)\pi x)$$ (1.20)

La détermination des coefficients $C_{k}$ est obtenue en imposant à la solution précédente de vérifier la condition initiale (ligne 23). Pour cela on vérifie que les fonctions élémentaires $Be$ sont orthogonales, i.e.:

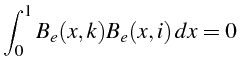$$\int_{0}^{1}B_{e}(x,k)B_{e}(x,i) dx=0$$   si  $$k\neq i$$

ce qui nous permet de déterminer les coefficients $C_{k}$ en multipliant la condition initiale par $B_{e}(x,k)$ et en intégrant sur l'intervalle $[0,1]$ (ligne 31).

La solution générale calculée à la ligne 34 est la fonction $U_{g}$ :

$$U_{g}:=(t,x)\mapsto$$

$$\sum_{k=0}^{N}2 \left(\int_{0}^{1}\! C(x)\cos(\frac{1}{2}\left(2... ...,\left(2 k+1\right)^{2}\pi^{2}Kt}\cos(\frac{1}{2}\left(2 k+1\right)\pi x)$$

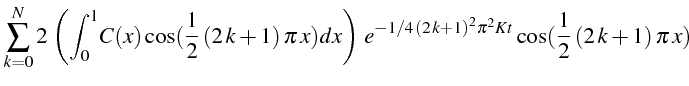Nous allons maintenant calculer explicitement cette solution générale dans les deux cas suivants:

1.3.3.1 cas 1: condition initiale gaussienne

La suite du programme Maple (1.3.3) pour le cas d'une condition initiale gaussienne $C(x)=e^{-(\frac{x}{\delta})^{2}}$ est donné ci dessous (programme 1.3.3). Il permet le calcul de la solution exacte en utilisant $N$ modes. Pour cette fonction $C(x)$ , Maple ne peut pas calculer analytiquement l'intégrale intervenant dans l'expression de $C_{k}$ (ligne 4), et nous utilisons la fonction Maple evalf pour obtenir une évaluation numérique des coefficients $C_{k}$ .

programme Maple 1.3.3: Solution analytique sur N modes de l'équation 1.1 pour la cas 1

# Etude du cas 1
> K:=1;delta:=1/10;C:=x->exp(-(x/delta)^2);
# calcul des coefficients de Fourier de la solution
> rel2;
> N:=20;
> for k from 0 to N do
>   C1[k]:=evalf(rhs(rel2));
> od:
# Trace des coefficients de Fourier en fonction du mode
> plot([seq([k,C1[k]],k=0..N)],title="coefficient de Fourier"):
# Solution sur N modes
> k:='k':
> Ue:=unapply(evalf(Ug(t,x)),t,x):
> t0:=1/(K*(Pi/2)^2);
> animate(Ue(t,x),x=0..1,t=0..t0,title="evolution temporelle");
> plot([Ue(0,x),Ue(t0/10,x),Ue(t0/4,x),Ue(t0,x)],x=0..1,
  title="Evolution temporelle de la solution exacte"
  ,legend=["t=0","t=t0/10","t=t0/4","t=t0"]);

1.3.3.2 cas 2 condition initiale créneau

Pour une condition initiale créneau $C(x)=Heaviside(\delta-x)$ , la suite du programme Maple (1.3.3) est donné ci dessous (programme 1.3.3). Il permet le calcul de la solution exacte en utilisant $N$ modes.

programme Maple 1.3.3: Solution analytique sur N modes de l'équation 1.1 pour le cas 2

# Etude du cas 2
> K:=1;delta:=1/10;C:=x->Heaviside(delta-x);
# Calcul des coefficients de Fourier de la solution
> eval(rel2);
> N:=1000;
> for k from 0 to N do
>   C1[k]:=evalf(rhs(rel2));
> od:
# Trace des coefficients de Fourier en fonction du mode
> plot([seq([k,C1[k]],k=0..N)],title="coefficient de Fourier");
# Solution sur N modes
> k:='k':
> Ue:=unapply(evalf(Ug(t,x)),t,x):
> t0:=1/(K*(Pi/2)^2);
> animate(Ue(t,x),x=0..1,t=0..t0,title="Evolution temporelle");
> plot([Ue(0,x),Ue(t0/10,x),Ue(t0/4,x),Ue(t0,x)],x=0..1,
   title="Evolution temporelle de la solution exacte"
   ,legend=["t=0","t=t0/10","t=t0/4","t=t0"]);
# Solution sur 20 modes
> N:=20:Ue1:=unapply(evalf(Ug(t,x)),t,x):
> plot([Ue1(0,x),Ue1(t0/10,x),Ue1(t0/4,x),Ue1(t0,x)],x=0..1);
> plot([Ue1(t0/100,x)-Ue(t0/100,x),Ue1(t0/10,x)-Ue(t0/10,x),
        Ue1(t0/4,x)-Ue(t0/4,x),Ue1(t0,x)-Ue(t0,x)],x=0..1,
  title="Erreur entre une solution sur N=20 et N=100"
  ,legend=["t=t0/100","t=t0/10","t=t0/4","t=t0"]);

Pour cette fonction, Maple peut calculer analytiquement les intégrales, et fournit l'expression exacte des coefficients $C_{k}$ (ligne 4).

$$C_{{k}}=4 {\frac{\sin(1/10 \pi k)\cos(1/20 \pi)+\cos(1/10 \pi k)\sin(1/20 \pi)}{\left(2 k+1\right)\pi}}$$ (1.21)

1.3.3.3 Analyse du cas 1: condition initiale gaussienne

Nous étudierons la solution sur un temps caractéristique $t_{0}$ de diffusion, qui pour notre problème vaut (ligne 15):

$$t_{0}=\frac{1}{\kappa\pi^{2}}$$

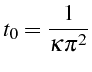
En effet, au bout de $t_{0}$ , l'amplitude de tous les modes décroît au moins d'un facteur $e^{-1/4}$ (un mode $k$ décroît d'un facteur de $e^{-(2k+1)^{2}/4}$ ).

Nous avons calculé l'amplitude des $N$ premiers modes (lignes 6 à 8), ainsi que la solution $U_{e}$ (ligne 13). Sur la figure (1.1), nous avons tracé le résultat pour $N=20$ modes et $K=1$ (lignes 10 et 17). Dans le programme Maple, on a aussi éffectué une animation de la solution à l'aide de la fonction animate (ligne 15).

Figure 1.1: Coefficients de Fourier (a) et évolution temporelle (b)

[coefficient $C_k$ ]

[$u(x,t)$ pour N=20]

On constate sur la figure (1.1a), que l'amplitude $C_{k}$ des modes décroît rapidement avec $k$ , et donc que la série de Fourier (ligne 13) converge rapidement (i.e. il suffit de peu de modes pour décrire la solution). Sur la figure (1.1b), on a tracé l'évolution temporelle de la solution analytique calculé sur $N$ modes. On constate bien l'amortissement de la solution initiale sur un temps de l'ordre de $t_{0}$ .

1.3.3.4 Analyse du cas 2: condition initiale créneau

Pour $N=1000$ , $K=1$ on a calculé l'amplitude et l'évolution temporelle de la solution, que l'on a tracé sur la figure 1.2.

Figure 1.2: Coefficients de Fourier (a) et évolution temporelle (b)

[$C_k$ ]

[$u(x,t)$ pour N=1000]

Contrairement au cas précédent, on constate sur la figure (1.2a), que la convergence de la série de Fourier est très lente, puisque l'amplitude des coefficients $C_{k}$ décroît très lentement vers zéro. C'est aussi ce que l'on remarque sur la figure (1.2b), où la solution initiale calculée avec $N=1000$ modes présente des oscillations sur les bords. C'est le phénomène classique de Gibbs, qui apparaît lorsque l'on approche une fonction discontinue (ici la fonction porte $C(x)=Heaviside(\delta-x)$ ) par une série de fonctions continues (ici les fonctions $B_{e}(x,k)=\cos(1/2 \left(2 k+1\right)\pi x))$ ). On remarque aussi que les solutions $U_{g}(x,t)$ pour $t>0$ ne présentent plus ses oscillations parasites. En effet les modes associés aux grandes valeurs de $k$ ont une amplitude qui décroît très rapidement avec $k$ (en $e^{-\frac{\kappa}{4}(\frac{2k+1}{\pi})^{2}t}$ ), et donc la série de Fourier converge très rapidement vers la solution $U_{g}(x,t)$ pour $t>0$ .

C'est ce que l'on vérifie en calculant la solution avec $N=20$ modes et la comparant à la solution calculée avec $N=1000$ modes (figure 1.3).

Figure 1.3: évolution temporelle (a) et écart entre la solution N=20 et N=1000 (b)

[$u(x,t)$ pour $N=20$ ]

[Ecart]

Sur la figure (1.3a), on a tracé l'évolution temporelle de la solution avec $N=20$ modes. On constate que, hormis la solution initiale, les solutions ressemblent aux solutions calculées avec $N=1000$ modes (figure 1.2b). Pour la solution initiale, elle présente plus d'oscillations que la solution avec $N=1000$ modes, ce qui confirme la faible convergence de la série de Fourier dans ce cas. Pour confirmer cette analyse, nous avons tracé sur la figure (1.3b), l'écart entre la solution calculée avec $N=20$ modes et celle avec $N=1000$ modes pour des valeurs de $t$ de $\frac{t_{0}}{100}$ à $t_{0}$ . On constate que l'erreur est très faible ( $2<10^{-10}$ ) et décroit avec $t$ , ce qui montre que la solution calculée avec $N=20$ modes est une très bonne approximation de la solution exacte pour $t>0$ .