1.4 Méthode des différences finies

Pour trouver une solution approchée du problème $(P_{1})$ ou $(P_{2})$ , nous allons construire une approximation par différences finies de l'équation de la chaleur (1.1).

Pour cela, le domaine de calcul $[0,L]$ est divisé en $N$ intervalles, chacun de longueur $\Delta x=\frac{L}{N}$ . Pour calculer la solution sur un temps $\tau$ , on découpe l'intervalle $[0,\tau]$ avec un pas $\Delta t$ . On calcul alors la solution approchée $u^{h}$ sur un maillage où chaque point d'indice $(i,n)$ $(x_{i},t_{n})$ est repéré sur l'axe $x$ par sa position $x_{i}=i\Delta x$ et sur l'axe $t$ par $t_{n}=n\Delta t$ comme le montre la figure 1.4

Figure 1.4: maillage différences finies

La solution approchée aux noeuds du maillage sera notée:

$$u^{h}(x_{i},t_{n})=u^{h}(i\Delta x,n\Delta t)=u_{i}^{n}$$ (1.22)

$$u^{h}(x_{i},t_{n+1})=u^{h}(i\Delta x,(n+1)\Delta t)=u_{i}^{n+1}$$

$$u^{h}(x_{i+1},t_{n})=u^{h}((i+1)\Delta x,n\Delta t)=u_{i+1}^{n}$$

$$u^{h}(x_{i-1},t_{n})=u^{h}((i-1)\Delta x,n\Delta t)=u_{i-1}^{n}\textrm{}$$

Pour approximer l'équation (1.1), nous allons chercher une approximation de la dérivée première en temps $\frac{\partial u}{\partial t}$ et de la dérivée seconde en espace $\frac{\partial^{2}u}{\partial x^{2}}$

1.4.1 Approximation de la dérivée première $\frac{\partial u}{\partial t}$

L'idée de base de la méthode des différences finies peut être décrite en partant de la définition de la dérivée première $\frac{\partial u}{\partial t}$ au point $x=x_{i}$ et à l'instant $t=t_{n}$ :

$$\frac{\partial u}{\partial t}=\underset{\Delta t\rightarrow0}{\lim}\frac{u(x_{i},t_{n}+\Delta t)-u(x_{i},t_{n})}{\Delta t}$$ (1.23)

Si la fonction $u(x,t)$ est régulière, on peut construire, à partir de cette relation (1.23), une approximation “raisonnable” de $\frac{\partial u}{\partial t}$ si $\Delta t$ est suffisamment petit.

$$\frac{\partial u}{\partial t}\approx\frac{u(x_{i},t_{n}+\Delta t)-u(x_{i},t_{n})}{\Delta t}$$ (1.24)

Pour préciser cette approximation, nous utiliserons le développement en série de Taylor de $u(x_{i},t_{n}+\Delta t)$ autour du point $\left(x_{i},t_{n}\right)$ à l'ordre m:

$$u(x_{i},t_{n}+\Delta t) = u(x_{i},t_{n})+\left.\frac{\Delta t}{1!}\frac{\partial u}{\partia... ...ac{\partial^{2}u}{\partial t^{2}}\right\vert _{\left(x_{i},t_{n}\right)}+\cdots$$ (1.25)

$$+\left.\frac{\Delta t^{m}}{m!}\frac{\partial^{m}u}{\partial t^{m}... ...elta t^{m+1}}{m+1!}\frac{\partial^{m+1}u}{\partial t^{m+1}}\right\vert _{\zeta} \notag$$ (1.26)

où $\zeta$ est un point dans l'intervalle $[t_{n},t_{n}+\Delta t]$ . Le dernier terme de ce développement peut être identifié à un reste d'ordre $O(\Delta t^{m+1})$ . En utilisant ce développement à l'ordre $m=2$ , nous pouvons en déduire l'approximation par différences finies de la dérivée première:

$$\left.\frac{\partial u}{\partial t}\right\vert _{\left(x_{i},t_{n... ...al^{2}u}{\partial t^{2}}\right\vert _{\left(x_{i},t_{n}\right)}+O(\Delta t^{2})$$ (1.27)

Dans le second membre de cette équation, on retrouve l'approximation par différences finies (1.24) plus un terme qui représente l'erreur liée à cette approximation, que l'on appelle erreur de troncature ( $E_{t}$ ). En passant à une notation $\left(i,n\right)$ nous pouvons écrire :

$$\left.\frac{\partial u}{\partial t}\right\vert _{i}^{n}=\underset... ...}{2!}\frac{\partial^{2}u}{\partial t^{2}}\right\vert _{i}^{n}+O(\Delta t^{2})}}$$ (1.28)

que l'on notera:

$$\left.\frac{\partial u}{\partial t}\right\vert _{i}^{n}=\frac{u_{i}^{n+1}-u_{i}^{n}}{\Delta t}+\underset{\text{$E_{t}$}}{\underbrace{O(\Delta t)}}$$ (1.29)

On obtiens ainsi une approximation de la dérivée première $\frac{\partial u}{\partial t}$ par différences finies à l'ordre 1:

$$\left.\frac{\partial u}{\partial t}\right\vert _{i}^{n}\approx\frac{u_{i}^{n+1}-u_{i}^{n}}{\Delta t}$$ (1.30)

L'erreur d'approximation de la dérivée première $\frac{\partial u}{\partial t}$ par la formule de différences finies (1.29) est une approximation d'ordre 1 en $\Delta t$ , ce qu'indique la notation $O\left(\Delta t\right)$ . Cette notation implique que $\left\vert E_{t}\right\vert\leq Cte\times\Delta t$ pour $\Delta t\rightarrow0$ .

Remarque : La notation $O(\Delta t)$ ne nous indique pas le comportement exact de la solution (la dérivée première dans ce cas), mais seulement la tendance lorsque $\Delta t\rightarrow0.$

D'autres représentations de la dérivée première peuvent être obtenues à partir de développements en série de Taylor. C'est ce que nous étudierons dans le chapitre suivant.

1.4.2 Approximation de la dérivée seconde $\frac{\partial^{2}u}{\partial x^{2}}$

Pour calculer l'approximation de la dérivée seconde, nous allons utiliser deux développements en série de Taylor de $u(x,t)$ au voisinage de $(x_{i},t_{n})$ :

1. le développement avancé en série de Taylor de $u(x_{i}+\Delta x,t_{n})$ :
   

   $$u(x_{i}+\Delta x,t_{n}) = u(x_{i},t_{n})+\left.\frac{\Delta x}{1!}\frac{\partial u}{\partia... ...{2!}\frac{\partial^{2}u}{\partial x^{2}}\right\vert _{\left(x_{i},t_{n}\right)}$$ (1.31)

   $$+ \left.\frac{\Delta x^{3}}{3!}\frac{\partial^{3}u}{\partial x^{3}}... ...ac{\partial^{4}u}{\partial x^{4}}\right\vert _{\left(x_{i},t_{n}\right)}+\cdots$$

   
   

2. le développement retardé en série de Taylor de $u(x_{i}-\Delta x,t_{n})$ :
   

   $$u(x_{i}-\Delta x,t_{n}) = u(x_{i},t_{n})-\left.\frac{\Delta x}{1!}\frac{\partial u}{\partia... ...{2!}\frac{\partial^{2}u}{\partial x^{2}}\right\vert _{\left(x_{i},t_{n}\right)}$$ (1.32)

   $$- \left.\frac{\Delta x^{3}}{3!}\frac{\partial^{3}u}{\partial x^{3}}... ...ac{\partial^{4}u}{\partial x^{4}}\right\vert _{\left(x_{i},t_{n}\right)}+\cdots$$

   
   

La somme de ces deux développements (1.30) et (1.31) nous donne l'approximation recherchée :

$$\left.\frac{\partial^{2}u}{\partial x^{2}}\ri... ...rac{\partial^{4}u}{\partial x^{4}}\right\vert _{i}^{n}+O(\Delta x^{4})}}$$

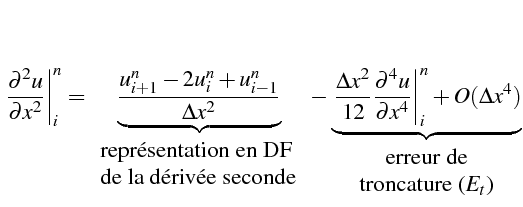
que l'on note aussi:

$$\left.\frac{\partial^{2}u}{\partial x^{2}}\right\vert _{i}^{n}=\frac{u_{i+1}^{n}-2u_{i}^{n}+u_{i-1}^{n}}{\Delta x^{2}}+O(\Delta x^{2})$$ (1.33)

ce qui fournit l'approximation de la dérivée seconde $\frac{\partial^{2}u}{\partial x^{2}}$ par différences finies à l'ordre 2:

$$\left.\frac{\partial^{2}u}{\partial x^{2}}\right\vert _{i}^{n}\approx\frac{u_{i+1}^{n}-2u_{i}^{n}+u_{i-1}^{n}}{\Delta x^{2}}$$ (1.34)

1.4.3 Un premier schéma aux différences finies: le schéma explicite

En remplaçant dans l'équation (1.1), la dérivée première en temps par son approximation par différences finies (1.29) et la dérivée seconde en espace par son approximation par différences finies (1.33), on obtient le schéma aux différences finies explicite:

$$\frac{u_{i}^{n+1}-u_{i}^{n}}{\Delta t}=\kappa \frac{u_{i+1}^{n}-2u_{i}^{n}+u_{i-1}^{n}}{\Delta x^{2}}$$ (1.35)

qui s'écrit:

$$u_{i}^{n+1}=u_{i}^{n}+r\left(u_{i+1}^{n}-2u_{i}^{n}+u_{i-1}^{n}\right)$$ (1.36)

en notant

$$r=\kappa\frac{\Delta t}{\Delta x^{2}}$$ (1.37)

La relation (1.35) permet de calculer explicitement la solution au temps $t_{n+1}=t_{n}+\Delta t$ en fonction de la solution au temps $t_{n}$ aux noeuds $i$ du maillage, sauf pour les 2 noeuds extrémités $i=0$ et $i=N$ . Pour ces deux noeuds, on utilise les conditions aux limites de $\left(P_{1}\right)$ :

$$u(0,t)=0 \Longrightarrow u_{0}^{n+1}=0$$

$$u(L,t)=0 \Longrightarrow u_{N}^{n+1}=0$$

Pour initialiser le calcul, on a besoin de la valeur de $u$ à $t=0$ aux noeuds du maillage $\left\{ u_{i}^{0}\right\}$ , qui est donnée par la condition initiale du problème $\left(P_{1}\right)$

$$u(x,0)=C(x) \Longrightarrow u_{i}^{0}=C(i \Delta x) \forall i=0,N$$

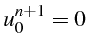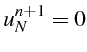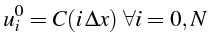Nous pouvons des à présent effectuer une simulation numérique en utilisant un tableur de type Excel. Pour cela on utilise un tableau de 5 colonnes et de 10 lignes, dont les cases sont repérées par des lettres pour les colonnes et des chiffres pour les lignes:

A1

B1

C1

D1

E1 A2

Le principe d'un tableur est de permettre des calculs en utilisant des relations entre les cases voisines qui, lorsque l'on les duplique ,sont automatiquement décalées (notation relative).

On choisit les paramètres du problème $\kappa=1, L=1, C(x)=sin(\pi x)$ et on discrétise le domaine $[0,1]$ en $N=4$ intervalles. La valeur du paramètre $r$ est choisie égale à $0,2$ .

Sur la première ligne du tableur (A1-E1), on rentre les coordonnées des $5$ points de maillage, et sur la deuxième ligne la condition initiale dans la colonne A avec la formule A2=sin(PI()*A1) , que l'on duplique dans les colonnes C à E. Sur la troisième ligne on calcule la solution au premier pas en temps $t=\Delta t$ en utilisant la formule déduite du schéma différences finies (1.35): B3=B2+0,2*(A2-2*B2+C2) pour la colonne B que l'on duplique dans les colonnes C à D. Pour les colonnes A et E on applique les conditions aux limites: A3=0 et E3=0 . Pour obtenir la solution aux pas en temps suivant, on duplique simplement les formules de la ligne 3 dans les lignes suivantes.

Le résultat des formules utilisées dans ce tableur est donnée dans le tableau ci-dessous:

0

1/4

1/2

3/4

1 sin(PI()*A1)

On obtient ainsi un tableau de valeurs qui fournit par ligne la solution numérique aux différents pas en temps. Le tableau (1.1) donne la valeur numérique de la solution calculée avec $r=0,2$ sur $10$ pas en temps.

Tableau 1.1: solution calculée pour $r=0,2$

t
X	0	1/4	1/2	3/4	1 0

Pour comparaison, on a donné la valeur de la solution exacte $u(x,t)=e^{-\pi^{2}t} \sin(\pi x)$ aux mêmes points de maillage et aux mêmes instants dans le tableau (1.2). En comparant les valeurs des deux tableaux, on constate que la solution par différences finies approxime bien la solution exacte (précision de 2 chiffres après la virgule).

Tableau 1.2: solution exacte

t
X	0	1/4	1/2	3/4	1 0,000
0,013	0,000	0,625	0,884	0,625	0,000
0,025	0,000	0,552	0,781	0,552	0,000
0,038	0,000	0,488	0,691	0,488	0,000
0,050	0,000	0,432	0,610	0,432	0,000
0,063	0,000	0,382	0,540	0,382	0,000
0,075	0,000	0,337	0,477	0,337	0,000
0,088	0,000	0,298	0,422	0,298	0,000
0,100	0,000	0,264	0,373	0,264	0,000
0,113	0,000	0,233	0,329	0,233	0,000

Par contre, si on refait le même calcul, mais avec une valeur de $r$ plus grande, par exemple $r=5$ on obtient le résultat donné dans le tableau (1.3).

Tableau 1.3: solution calculée pour $r=5$

t
X	0	1/4	1/2	3/4	1 0,000
0,313	0,000	-1,364	-1,929	-1,364	0
0,625	0,000	2,631	3,721	2,631	0
0,938	0,000	-5,075	-7,177	-5,075	0
1,250	0,000	9,789	13,844	9,789	0
1,563	0,000	-18,883	-26,705	-18,883	0
1,875	0,000	36,424	51,511	36,424	0
2,188	0,000	-70,259	-99,362	-70,259	0
2,500	0,000	135,525	191,662	135,525	0
2,813	0,000	-261,419	-369,703	-261,419	0

On constate que pour cette valeur de $r$ , la solution numérique diverge avec des valeurs $u_{i}^{n}$ de plus en plus grandes. De ces essais numériques, on peut en déduire que pour les petites valeurs de $r$ , la solution numérique converge vers la solution exacte, mais que pour les grandes valeurs de $r$ la solution numérique diverge.

Cette approche expérimentale est démonstrative et empirique. Une approche systèmatique consiste à faire une analyse numérique des schémas aux différences finies pour connaître à priori les conditions de convergence et les propriétés de la solution numérique.