suivant: 1.6 Validation avec Matlab monter: 1. Une première approche précédent: 1.4 Méthode des différences Table des matières
Pour étudier la convergence de la solution numérique
![]() du schéma aux différences finies (1.34) vers la solution
exacte
du schéma aux différences finies (1.34) vers la solution
exacte
![]() de l'équation (1.1), on peut soit essayer
d'étudier directement la convergence, ce qui peut être compliqué et
pas toujours possible, soit utiliser un résultat d'analyse du à Lax
(Richtmyer et Norton 1967):
de l'équation (1.1), on peut soit essayer
d'étudier directement la convergence, ce qui peut être compliqué et
pas toujours possible, soit utiliser un résultat d'analyse du à Lax
(Richtmyer et Norton 1967):
|
|
La consistance et la stabilité d'un schéma sont en général beaucoup plus facile à étudier que sa convergence.
La consistance caractérise la façon dont l'équation aux différences finies (EDF) approche l'équation aux dérivées partielles (EDP).
ce qui donne, compte tenu du fait que
![]()
Cette différence est l'erreur de troncature du schéma aux différences
finies, et corresponds donc à l'erreur commise lorsque l'on remplace
la solution approchée
![]() par la solution exacte aux noeuds
du maillage
par la solution exacte aux noeuds
du maillage
![]() dans l'équation aux différences
EDF.
dans l'équation aux différences
EDF.
Le schéma EDF est dit consistant à l'équation EDP si cette erreur
de troncature tends vers zéro lorsque le pas de discrétisation en
temps
![]() et le pas de discrétisation en espace
et le pas de discrétisation en espace
![]() tendent vers zéro indépendamment.
tendent vers zéro indépendamment.
![\bgroup\color{black}$\displaystyle \lim_{\Delta x\rightarrow0, \Delta t\rightarrow0}E_{t}=EDF[u(i\Delta x,n\Delta t)]=0$\egroup](img407.png)
Appliquons cette définition au schéma explicite (1.34), en
notant
![]() la solution exacte aux
noeuds du maillage:
la solution exacte aux
noeuds du maillage:
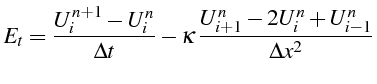
Pour calculer cette erreur de troncature, on exprime toutes les quantités
en fonction de
![]() en effectuant des développement en série
de Taylor au voisinage du point
en effectuant des développement en série
de Taylor au voisinage du point
![]() :
:
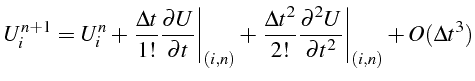 |
|
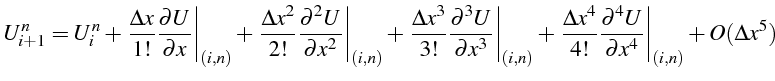 |
|
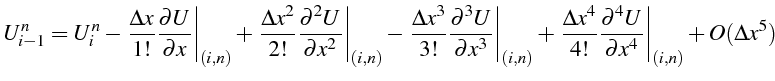 |
En reportant ces développements dans l'erreur de troncature , il vient
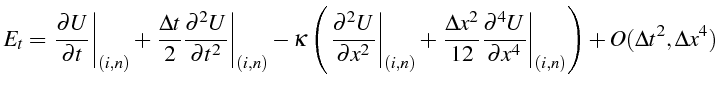
On utilise ensuite le fait que
![]() vérifie l'équation exacte
au point
vérifie l'équation exacte
au point
![]()
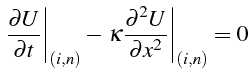
ce qui donne l'expression de l'erreur de troncature du schéma explicite:
Cette erreur de troncature tends bien vers zéro, lorsque
![]() et
et
![]() tendent vers zéro indépendamment.
tendent vers zéro indépendamment.
Le schéma explicite 1.34 est donc consistant à l'équation
de la chaleur (1.1) et l'erreur de troncature est en
![]() ,
i.e. d'ordre 1 en temps et d'ordre 2 en espace.
,
i.e. d'ordre 1 en temps et d'ordre 2 en espace.
L'ordre de troncature est aussi la précision de la solution numérique,
i.e l'erreur entre la solution numérique
![]() et la solution
exacte
et la solution
exacte
![]() est en
est en
![]() .
.
Remarque: on peut transformer l'erreur de troncature
(1.37) en dérivant l'équation exacte par rapport à
t pour calculer
![]() :
:
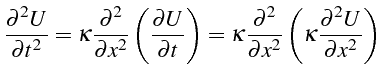
En remplaçant dans (1.37) il vient:
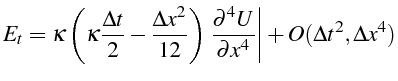
on remarque que pour la valeur particulière de
![]() telle
que:
telle
que:
le premier terme de l'erreur de troncature s'annulle, et la
précision du schéma augmente pour être en
![]() .
.
La notion de stabilité s'applique à des schèmas, pour lesquels on calcule des solutions de façon itérative. Les calculs s'éffectuent sur des ordinateurs avec une précision finie, et donc sont sujet à des erreurs d'arrondis. Lors d'un calcul itératif, ces erreurs peuvent être amplifiées par le schèma numérique. Le but de l'étude de stabilité est donc de déterminer quelle est l'amplification des erreurs (ou perturbations) par le schèma.
Soit
![]() une perturbation de la solution à l'étape
une perturbation de la solution à l'étape
![]() . La solution perturbée
. La solution perturbée
![]() à l'étape
à l'étape
![]() est solution de l'équation aux différences:
est solution de l'équation aux différences:
L'équation sur la perturbation est obtenue en effectuant la différence (1.40)-(1.39):
On décompose cette perturbation en tout point
![]() du
maillage et à tout instant
du
maillage et à tout instant
![]() sous la forme d'une série de modes
de Fourier (en notant
sous la forme d'une série de modes
de Fourier (en notant
![]() ):
):
Le problème étant linéaire, chacun des modes vérifie l'équation (1.41),
qui s'écrit pour un mode
![]() :
:
En posant
![]() et en utilisant les
relations trigonométriques
et en utilisant les
relations trigonométriques
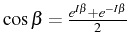 et
et
![]() l'équation (1.44) devient :
l'équation (1.44) devient :
Il est clair que si l'amplitude
![]() de chaque
mode de la perturbation diminue d'une itération à l'autre, l'erreur
décroît et la perturbation finit par disparaître. Ceci se traduit
par la condition:
de chaque
mode de la perturbation diminue d'une itération à l'autre, l'erreur
décroît et la perturbation finit par disparaître. Ceci se traduit
par la condition:
qui doit être vérifiée pour chaque mode
![]() , i.e.
, i.e.
![]() c'est à dire
c'est à dire
![]() .
.
Dans l'équation (1.46) on note par
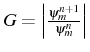 le facteur d'amplification du schèma.
le facteur d'amplification du schèma.
Remarque: cette analyse de stabilité n'a pas prise
en compte les conditions aux limites. Le type des conditions aux limites
et leurs discrétisations sélectionnent certains modes de Fourier.
Dans notre étude, la condition aux limites sur la perturbation est
une condition homogéne de Dirichlet:
![]() ,
et elle impose des modes de Fourier en
,
et elle impose des modes de Fourier en
![]() pour vérifier ces conditions aux limites ( i.e.
pour vérifier ces conditions aux limites ( i.e.
![]() ).
On verra à la fin du chapitre une autre façon de faire l'analyse de
stabilité: l'approche matricielle qui prend en compte directement
les conditions aux limites.
).
On verra à la fin du chapitre une autre façon de faire l'analyse de
stabilité: l'approche matricielle qui prend en compte directement
les conditions aux limites.
L'inégalité (1.46), s'écrit:
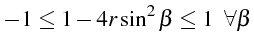
soit
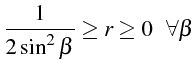
Cette inégalité impose une valeur maximale à
![]() :
:
Le schèma explicite est donc conditionnellement stable, avec un critère de stabilité donné par la condition:
Cette condition s'utilise de la façon suivante: on fixe le maillage
en espace, i.e. le pas
![]() et le pas en temps d'intégration
en temps
et le pas en temps d'intégration
en temps
![]() doit alors être choisi tel que:
doit alors être choisi tel que:
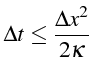
On remarque que plus on augmente le nombre de points en espace (i.e.
plus
![]() diminue), plus il faut prendre un pas en temps
diminue), plus il faut prendre un pas en temps
![]() petit. C'est l'un des principales inconvénients de ce schéma explicite.
petit. C'est l'un des principales inconvénients de ce schéma explicite.
Pour ce schéma explicite, il est possible d'étudier directement la convergence de la solution numérique vers la solution exacte. Pour cela nous allons déterminer la solution exacte de l'équation aux différences finies (1.35):
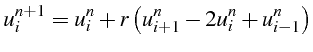
Par analogie avec la solution exacte (1.17), nous allons
chercher une solution
![]() sous la forme d'une série:
sous la forme d'une série:
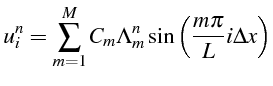
où les coefficients
![]() donnent la dépendance temporelle
et les
donnent la dépendance temporelle
et les
![]() prennent en compte la condition initiale.
prennent en compte la condition initiale.
En notant
![]() le nombre d'intervalle en espace, on a
le nombre d'intervalle en espace, on a
![]() et la série s'écrit:
et la série s'écrit:
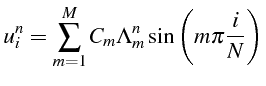
Cette série discréte ne comprends que
![]() modes indépendants.
En effet pour
modes indépendants.
En effet pour
![]() , le mode
, le mode
![]() est confondu aux noeuds du maillage
avec un mode
est confondu aux noeuds du maillage
avec un mode
![]() tel que
tel que
![]() , puisque:
, puisque:
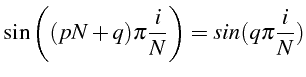
et pour
![]() on a un mode identiquement nul. Ce nombre de modes
on a un mode identiquement nul. Ce nombre de modes
![]() est en fait le nombre de degrés de liberté de la solution
numérique:
est en fait le nombre de degrés de liberté de la solution
numérique:
![]() est définie par
est définie par
![]() valeurs
aux points de maillage, mais on impose 2 conditions aux limites
valeurs
aux points de maillage, mais on impose 2 conditions aux limites
![]() et
et
![]() , ce qui donne en définitive
, ce qui donne en définitive
![]() degrés de liberté.
degrés de liberté.
La solution
![]() s'écrit donc:
s'écrit donc:
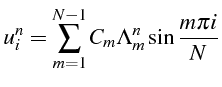
Le problème étant linéaire, chacun des modes est solution de l'équation
(1.35), ce qui donne en simplifiant par
![]() qui ne dépend
ni de
qui ne dépend
ni de
![]() ni de
ni de
![]() :
:
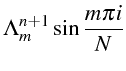 |
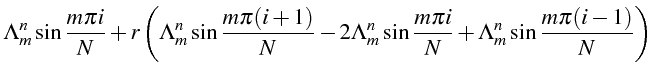 |
||
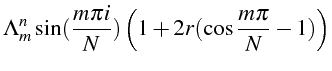 |
|||
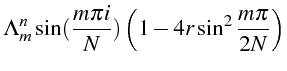 |
d'où le coefficient
![]()
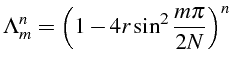
Les coefficients
![]() sont déterminés de façon à vérifier la condition
initiale aux noeuds du maillage
sont déterminés de façon à vérifier la condition
initiale aux noeuds du maillage
![]() :
:
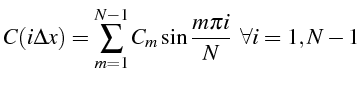
Ce sont donc les coefficients de la transformée de Fourier de la condition
initiale
![]() calculée aux noeuds du maillage:
calculée aux noeuds du maillage:
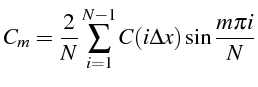
La solution numérique s'écrit donc:
Comparons cette solution à la solution exacte (1.17) aux
noeuds du maillage. La solution exacte au point
![]() et
à
et
à
![]() s'écrit, en remplaçant
s'écrit, en remplaçant
![]() et
et
![]() en fonction de
en fonction de
![]() et
et
![]() :
:
En comparant les deux expressions (1.49) et (1.50),
on voit que pour montrer la convergence de
![]() vers
vers
![]() ,
il faut montrer que
,
il faut montrer que
![]() tends vers
tends vers
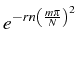 .
Attention, on se place en un point
.
Attention, on se place en un point
![]() fixe et à un instant
fixe et à un instant
![]() fixé. Donc lorsque l'on fait tendre
fixé. Donc lorsque l'on fait tendre
![]() et
et
![]() vers zéro, les indices
vers zéro, les indices
![]() et
et
![]() augmentent en fonction
de
augmentent en fonction
de
![]() et
et
![]() . On introduit alors un petit paramètre
. On introduit alors un petit paramètre
![]() , et on effectue les développements
limités par rapport à
, et on effectue les développements
limités par rapport à
![]() de
de
![]() :
:
et de
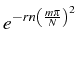 :
:
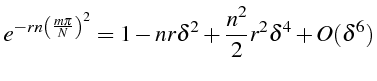
L'écart entre ces 2 développements s'écrit en remplaçant
![]() et
et
![]() en fonction de
en fonction de
![]() et
et
![]() et en notant que
et en notant que
![]() :
:
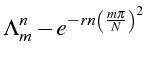 |
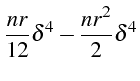 |
||
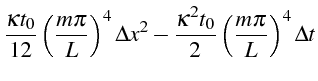 |
Cet écart tend bien vers zéro lorsque
![]() et
et
![]() tendent
vers zéro, et est d'ordre 2 en espace et d'ordre 1 en temps.
tendent
vers zéro, et est d'ordre 2 en espace et d'ordre 1 en temps.
A partir de l'expression (1.49), on peut aussi en déduire
le comportement de la solution numérique. Pour chaque mode
![]() de
cette solution, on approxime la dépendance temporelle en exponentielle
décroissante de la solution exacte par une fonction puissance
de
cette solution, on approxime la dépendance temporelle en exponentielle
décroissante de la solution exacte par une fonction puissance
![]() .
Pour qu'il y ait convergence, il faut donc que
.
Pour qu'il y ait convergence, il faut donc que
![]() (c'est aussi la condition pour que le développement limité 1.51
converge). Cette condition implique:
(c'est aussi la condition pour que le développement limité 1.51
converge). Cette condition implique:
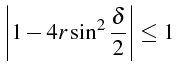
qui est justement la condition de stabilité (1.47) du schéma explicite:
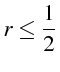
Nous avons tracé sur la figure (1.5) le facteur d'amplification
![]() du mode
du mode
![]()
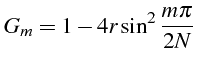
en fonction de
![]() et pour différentes valeurs de
et pour différentes valeurs de
![]() .
.
On note que ce facteur d'amplification est positif et inférieure à
1 pour les petits nombres d'ondes
![]() , et donc les grandes longueurs
d'ondes
, et donc les grandes longueurs
d'ondes
![]() sont toujours amorties comme pour la solution
exacte. Par contre le comportement des petites longueurs d'ondes (i.e.
des grandes nombres d'ondes
sont toujours amorties comme pour la solution
exacte. Par contre le comportement des petites longueurs d'ondes (i.e.
des grandes nombres d'ondes
![]() ) dépend de
) dépend de
![]() .
.
Pour
![]() , le facteur d'amplification des grands nombres
d'ondes
, le facteur d'amplification des grands nombres
d'ondes
![]() est négatif et inférieure à
est négatif et inférieure à
![]() , donc les petites longueurs
d'ondes se mettent à osciller avec une amplitude croissante et le
schéma diverge. La divergence du schéma explicite se traduit donc
par l'apparition d'oscillations à hautes fréquences d'amplitudes croissantes.
, donc les petites longueurs
d'ondes se mettent à osciller avec une amplitude croissante et le
schéma diverge. La divergence du schéma explicite se traduit donc
par l'apparition d'oscillations à hautes fréquences d'amplitudes croissantes.
Pour
![]() , le facteur d'amplification des
grands nombres d'ondes
, le facteur d'amplification des
grands nombres d'ondes
![]() est négatif, mais supérieure à
est négatif, mais supérieure à
![]() ,
donc les petites longueurs d'ondes se mettent aussi à osciller mais
avec une amplitude décroissante et le schéma ne diverge pas. La solution
numérique peut présenter des oscillations, mais qui décroissent au
cours du temps.
,
donc les petites longueurs d'ondes se mettent aussi à osciller mais
avec une amplitude décroissante et le schéma ne diverge pas. La solution
numérique peut présenter des oscillations, mais qui décroissent au
cours du temps.
Pour
![]() , le facteur d'amplification des grands nombres
d'ondes
, le facteur d'amplification des grands nombres
d'ondes
![]() reste toujours positif, et les petites longueurs d'ondes
décroissent de façon monotone, comme dans la solution exacte.
reste toujours positif, et les petites longueurs d'ondes
décroissent de façon monotone, comme dans la solution exacte.
Cette étude nous a donc fournit un renseignement supplémentaire
par rapport à l'étude de stabilité: si on veut une convergence monotone
de la solution numérique vers la solution exacte, il faut choisir
![]() .
.