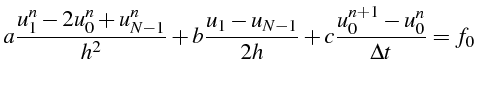suivant: 2.6 Convergence monter: 2. Construction de schéma précédent: 2.4 Exemple d'obtention de Table des matières
Ayant vu comment approcher les dérivées par des différences finies, l'approximation de l'équation à résoudre est obtenue en remplaçant les dérivées exactes par leurs approximations par différences finies.
Pour l'équation modèle (2.1), avec des différences finies centrées explicites, il vient l'équation discréte:
Cette équation sera noté symboliquement
Il reste cependant à appliquer les conditions aux limites sur la solution approchée. Pour les EDP du second ordre, les conditions aux limites peuvent être du type Dirichlet, Neuman ou Mixte.
Cette condition consiste à imposer la valeur de la solution sur la
frontière:
![]() , ce qui est se traduit par l'imposition
de la valeur nodale
, ce qui est se traduit par l'imposition
de la valeur nodale
![]() .
.
Cette condition impose la valeur de la dérivée normale de la solution
![]() . Pour l'imposer en différences
finies, il faut discrétiser cette condition de Neuman.
. Pour l'imposer en différences
finies, il faut discrétiser cette condition de Neuman.
![\includegraphics[width=0.6\textwidth]{CHAP2/climite}](img876.png)
Nous étudierons deux façons d'imposer cette condition aux limites de type Neumann:
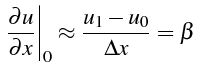 |
(2.50) |
| (2.51) |
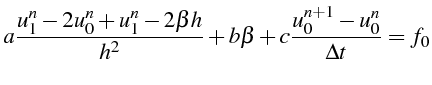
Cette condition impose une relation entre la valeur et la dérivée normale de la solution:
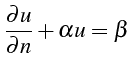
Elle se traite en différences finies comme une condition de type Neuman, soit en discrétisant directement la condition aux limites, soit en introduisant un point fictif.
Si la solution est périodique en espace sur
![]() , elle vérifie
alors les deux conditions:
, elle vérifie
alors les deux conditions:
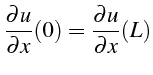
Ces conditions sont alors imposées en utilisant un point fictif pour
![]() (condition miroir)
(condition miroir)
ce qui fournit l'équation pour le noeud
![]() :
: