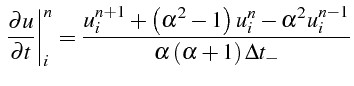suivant: 2.5 Equations discrétes et monter: 2. Construction de schéma précédent: 2.3 Polynôme d'interpolation Table des matières
Supposons que nous cherchons à déterminer l'approximation en DF de
la dérivée première
![]() avec une erreur de troncature de l'ordre de
avec une erreur de troncature de l'ordre de
![]() en utilisant
trois points consécutifs à savoir
en utilisant
trois points consécutifs à savoir
![]()
![]() et
et
![]() .
.
Il existe plusieurs façon d'obtenir le résultat:
Après substitution et ré-arrangement, on peut en déduire l'expression suivante :
En remplaçant dans l'équation (2.44)
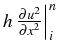 , par son expression tirée de l'équation (2.45), nous obtenons
la relation recherchée. Nous pouvons procéder, pour obtenir cette
relation, par combinaison des équations de la manière suivante :
, par son expression tirée de l'équation (2.45), nous obtenons
la relation recherchée. Nous pouvons procéder, pour obtenir cette
relation, par combinaison des équations de la manière suivante :
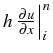 serait égal à
serait égal à 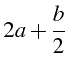 |
0 |
donne
![]() et
et ![]()
de sorte que l'équation
donne :
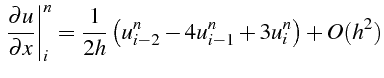
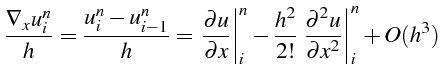
que l'on peut corriger à l'ordre 2:
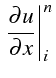 |
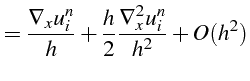 |
|
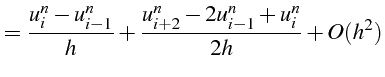 |
qui fournit la relation précédente
Comme exemple plus élaboré, nous cherchons à développer l'approximation
en DF pour la dérivée
![]() , avec une erreur
, avec une erreur
![]() , en utilisant une discrétisation à trois points
centrée autour du point
, en utilisant une discrétisation à trois points
centrée autour du point
![]() , c'est à dire
en utilisant les variables
, c'est à dire
en utilisant les variables
![]()
![]() et
et
![]() Pour un maillage non uniforme, on adoptera les notations suivantes:
Pour un maillage non uniforme, on adoptera les notations suivantes:
Pour
![]() nous avons :
nous avons :
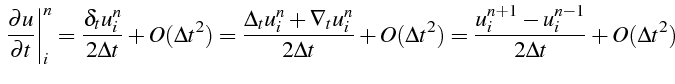
Posons
![]() et prenons
une notation plus compacte
et prenons
une notation plus compacte
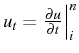
Comme précédemment, nous devons multiplier ces deux expressions
par les coefficients
![]() et
et
![]() additionner les deux relations
puis extraire
additionner les deux relations
puis extraire
![]() En cherchant à imposer le coefficient devant
En cherchant à imposer le coefficient devant
![]() égal à
égal à
![]() , après l'addition, on obtient :
, après l'addition, on obtient :
Par ailleurs, pour que le résultat finale possède une erreur
de troncature
![]() ou supérieure, le coefficient devant
ou supérieure, le coefficient devant
![]() doit être égal à zéro après l'addition, ce qui exige que
:
doit être égal à zéro après l'addition, ce qui exige que
:
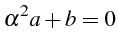
La solution de ces deux équations algébriques est :
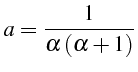 et
et 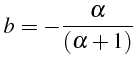
Par conséquent
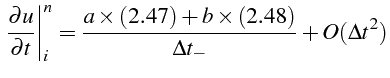
d'où le résultat