suivant: 2.4 Exemple d'obtention de monter: 2. Construction de schéma précédent: 2.2 Approximation des dérivées Table des matières
Une autre façon de construire des approximations de dérivée est d'utiliser un polynôme d'interpolation, puis de le dériver.
Soient
![]() points d'interpolation
points d'interpolation
![]() associés à
associés à
![]() valeurs
valeurs
![]()
soit
![]() l'espace vectoriel des polynômes de degré
l'espace vectoriel des polynômes de degré
![]()
soit
![]() le polynôme de Lagrange de
le polynôme de Lagrange de
![]() t.q.
t.q.
![]()
![]() possède n zéros
possède n zéros
![]() pour
pour
![]() et vaux
et vaux
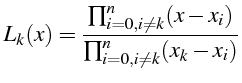
les
![]() forment une base de
forment une base de
![]()
le polynôme d'interpolation passant par les
![]() points d'interpolation
points d'interpolation
![]() associés à
associés à
![]() valeurs
valeurs
![]() vérifie:
vérifie:
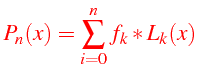 |
(2.39) |
L'erreur entre la fonction exacte
![]() et son polynôme d'interpolation
et son polynôme d'interpolation
![]() est donnée par le théorème suivant:
est donnée par le théorème suivant:
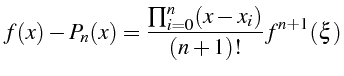 avec
avec
Soit
![]() et
et
![]()
W(t) s'annule en n+2 points :
![]() (i=0,n) et x
(i=0,n) et x
donc W'(t) s'annule en n+1 points (théorème de Rolle)
donc
![]() s'annule une fois en
s'annule une fois en
![]()
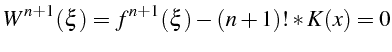
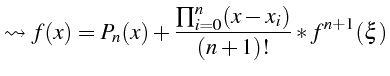
![\bgroup\color{black}$\displaystyle \left\vert f(x)-P_{n}(x)\right\vert\leq\frac{...
...\vert}{(n+1)!}\underset{x\in[a,b]}{\sup}\left\vert f^{n+1}(x)\right\vert$\egroup](img777.png)
soit une erreur en
![]()
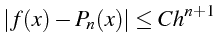
Le polynôme d'interpolation
![]() de degré 1 passant par les
points
de degré 1 passant par les
points
![]() s'écrit:
s'écrit:
Le polynôme d'interpolation
![]() de degré 2 passant par les
points
de degré 2 passant par les
points
![]() s'écrit:
s'écrit:
Partant de l'expression du polynôme d'interpolation de Lagrange
![]() aux points de collocations
aux points de collocations
![]()
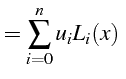 avec avec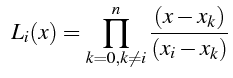 |
La dérivée première est:
et la dérivée seconde:
Ces expressions permettent d'évaluer les valeurs des dérivées aux
points de collocation
![]() .
.
Si on dérive le polynôme
![]() (2.41), on obtiens un
formule équivalente à la dérivée centrée d'ordre 2 (2.15)
(2.41), on obtiens un
formule équivalente à la dérivée centrée d'ordre 2 (2.15)
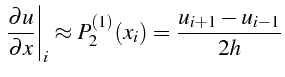
De même, on dérive le polynôme
![]() (2.40), on obtiens
un formule équivalente à la dérivée décentrée d'ordre 1 (2.11)
(2.40), on obtiens
un formule équivalente à la dérivée décentrée d'ordre 1 (2.11)
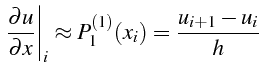
La dérivée seconde du polynôme d'interpolation
![]() de degré
2:
de degré
2:
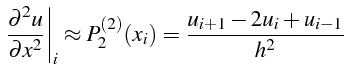
Les expressions (2.42),(2.43), très lourdes à manipuler,
s'avèrent utiles pour évaluer les valeurs des dérivées aux points
de collocation
![]() . Le polynôme
. Le polynôme
![]() est une combinaison
linéaire des valeurs nodales
est une combinaison
linéaire des valeurs nodales
![]() , donc il en est de même pour
toutes ses dérivées
, donc il en est de même pour
toutes ses dérivées
![]() . Les valeurs nodales de ces dérivées
. Les valeurs nodales de ces dérivées
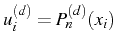 s'expriment ainsi comme combinaisons
linéaires des
s'expriment ainsi comme combinaisons
linéaires des
![]() . Ce système peut donc s'écrire sous la forme
matricielle:
. Ce système peut donc s'écrire sous la forme
matricielle:
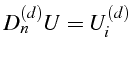
où
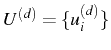 et
et
![]() sont les vecteurs
contenant respectivement les valeurs aux points de collocation des
dérivées (d'ordre
sont les vecteurs
contenant respectivement les valeurs aux points de collocation des
dérivées (d'ordre
![]() )
)
![]() et des valeurs nodales
et des valeurs nodales
![]() ,
et
,
et
![]() est la matrice de dérivation (d)ème dont les éléments
sont:
est la matrice de dérivation (d)ème dont les éléments
sont:
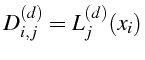
Ainsi, pour un stencil de 3 points équi-distants (espacés de
![]() )
)
![]() , les matrices de dérivation d'ordre 1
, les matrices de dérivation d'ordre 1
![]() et d'ordre 2
et d'ordre 2
![]() s'écrivent:
s'écrivent:
![\bgroup\color{black}$\displaystyle D^{(1)}=\frac{1}{2h}\left[\begin{array}{ccc}
-3 & 4 & -1\\
1 & 0 & -1\\
1 & -4 & 3\end{array}\right]$\egroup](img814.png)
![\bgroup\color{black}$\displaystyle D^{(2)}=\frac{1}{h^{2}}\left[\begin{array}{ccc}
1 & -2 & 1\\
1 & -2 & 1\\
1 & -2 & 1\end{array}\right]$\egroup](img815.png)
On retrouve les formules de dérivée centrée d'ordre 1 et d'ordre 2
en calculant la dérivée au noeud milieu
![]() : pour la dérivée
première
: pour la dérivée
première
![\bgroup\color{black}$ u_{i}^{(1)}=D_{2,i}^{(1)} [u_{i-1},u_{i},u_{i+1}]^{t}$\egroup](img816.png) et la dérivée seconde
et la dérivée seconde
![\bgroup\color{black}$ u_{i}^{(2)}=D_{2,i}^{(2)} [u_{i-1},u_{i},u_{i+1}]^{t}$\egroup](img817.png)