suivant: 2.3 Polynôme d'interpolation monter: 2. Construction de schéma précédent: 2.1 Problème modèle Table des matières
Afin d'appliquer la méthode des différences finies, le domaine spatiale
![]() doit être divisé en
doit être divisé en
![]() intervalles, chacun de longueur
intervalles, chacun de longueur
![]() . Le domaine temporelle est aussi divisée en
. Le domaine temporelle est aussi divisée en
![]() intervalles
de pas
intervalles
de pas
![]() . Le domaine
. Le domaine
![]() est donc découpé
suivant un maillage où chaque point
est donc découpé
suivant un maillage où chaque point
![]() est repéré sur l'axe
est repéré sur l'axe
![]() par sa position
par sa position
![]() et sur l'axe
et sur l'axe
![]() par
par
![]() comme le montre la figure ci dessous.
comme le montre la figure ci dessous.
On pose dans ce qui suit :
| (2.2) | ||
| (2.3) | ||
| (2.4) | ||
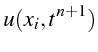 |
(2.5) |
L'idée de base de la méthode des différences finis peut être décrite
en considérant la définition de la dérivée d'une fonction
![]() au point
au point
![]() et à l'instant
et à l'instant
![]()
Si
![]() est continue, on peut s'attendre à ce que l'équation
(2.6) soit une approximation ”raisonnable” de
est continue, on peut s'attendre à ce que l'équation
(2.6) soit une approximation ”raisonnable” de
![]() si
si
![]() est suffisamment petit. Le
développement en série de Taylor de
est suffisamment petit. Le
développement en série de Taylor de
![]() autour du
point
autour du
point
![]() donne :
donne :
où
![]() et où le dernier
terme peut être identifié comme étant le reste. Nous pouvons alors
former les différences avancées en réarrangeant l'équation (2.7).
et où le dernier
terme peut être identifié comme étant le reste. Nous pouvons alors
former les différences avancées en réarrangeant l'équation (2.7).
En passant à une notation
![]() nous pouvons
écrire :
nous pouvons
écrire :
On peut aussi écrire l'équation (2.10) comme suit :
L'écriture de l'erreur de troncature en
![]() implique que
implique que
![]() pour
pour
![]() et
et
![]()
Remarque :
![]() ne nous indique pas le comportement
exacte de la solution (la dérivée première dans ce cas), mais seulement
la tendance lorsque
ne nous indique pas le comportement
exacte de la solution (la dérivée première dans ce cas), mais seulement
la tendance lorsque
![]()
D'autres représentation de la dérivée première peuvent être obtenues à partir de développement en série de Taylor.
Un développement en série de Taylor de
![]() :
:
permet de définir l'approximation décentrée retardée:
En faisant la différence entre l'équation (2.11) et l'équation (2.14), nous obtenons l'expression de la différenciation centrée qui s'écrit :
Soit le développement avancé en série de Taylor :
De même le développement retardé en série de Taylor s'écrit :
La somme des l'équation (2.16) et (2.17) donne :
On définit maintenant les opérateurs de différenciation décentrée avancée et retardée:
Les opérateurs de différenciation centrée s'écrivent :
et l'opérateur moyenne :
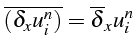
Il est intéressant d'avoir des opérateurs spécifiques pour certaines différences centrées. Deux de ces opérateurs peuvent s'écrire en fonction des opérateurs données ci-dessus.
En utilisant ces nouveaux opérateurs, les différences centrées pour la dérivée première s'écrivent :
et pour la dérivée seconde :
Les opérateurs de différenciation avancée ou retardée, d'ordre plus élevé sont définis en appliquant successivement ces opérateurs :
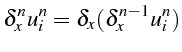
Exemple :
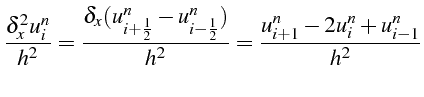
On peut écrire d'une façon générale la discrétisation d'une
dérivée d'ordre
![]() , en utilisant ces différents opérateurs, nous
obtenons alors :
, en utilisant ces différents opérateurs, nous
obtenons alors :
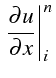 |
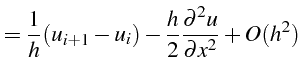 |
|
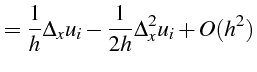 |
||
 |
Notons que la plupart des équations de la mécanique contiennent des dérivées premières et secondes. Les expressions sur 3 points des dérivées premières les plus utilisées sont :
| dérivée | opérateur D.F. | approximation D.F. | précision
|
|---|
Pour la dérivée seconde :
| dérivée | opérateur D.F. | approximation D.F. | précision
|
|---|
Pour obtenir des schémas d'ordre plus élevé, on peut augmenter le nombre de points de calcul, mais on peut aussi conserver des schémas compactes en introduisant des inconnues supplémentaires
On choisie comme inconnues les dérivées
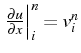 .
Les développements en série de Taylor de
.
Les développements en série de Taylor de
![]() et
et
![]() s'écrivent:
s'écrivent:
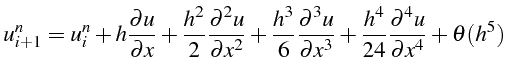
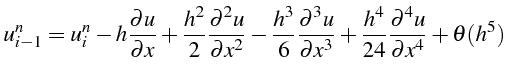
d'où l'approximation à l'ordre
![]() de
de
![]()
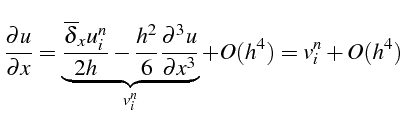
On note que
![]() est la dérivée
seconde de
est la dérivée
seconde de
![]() et peut être approximée par
et peut être approximée par
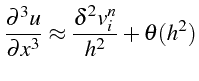
d'où la relation
qui s'écrit:
L'équation (2.36) fournit une relation implicite
pour le calcul de
![]() qui peut donc être déterminée en résolvant
le système algébrique tri-diagonale (les
qui peut donc être déterminée en résolvant
le système algébrique tri-diagonale (les
![]() étant supposées
connues):
étant supposées
connues):
![\bgroup\color{black}$\displaystyle \left[\begin{array}{ccccc}
\ddots & \ddots\ ...
...\
\frac{u_{i+1}^{n}-u_{i-1}^{n}}{2h}\\
\vdots\\
\ \end{array}\right]$\egroup](img694.png)
soit
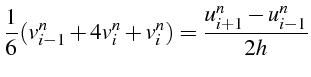
En posant
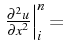
![]() , on peut obtenir une approximation d'ordre 4 de la dérivée
seconde:
, on peut obtenir une approximation d'ordre 4 de la dérivée
seconde:
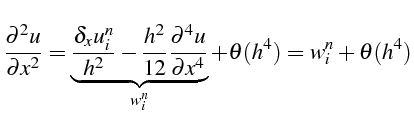
dans laquelle on calcule
![]() avec une approximation de la dérivée seconde de
avec une approximation de la dérivée seconde de
![]() :
:
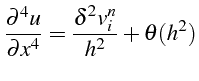
D'où le schéma compact pour la dérivée seconde:
qui nécessite aussi la résolution d'un système tri-diagonal
pour déterminer les
![]()
| Dérivée | opérateur D.F. | approximation DF | ordre
|
|---|
Des relations pouvant impliquer plus de trois points de
maillage peuvent être obtenues en utilisant des développements en
série de Taylor de
![]() ,
,
![]() ,
,
![]() et
et
![]() , ou en corrigeant l'erreur de troncature des schémas
précédents. Par exemple le schéma décentré amont d'ordre 1:
, ou en corrigeant l'erreur de troncature des schémas
précédents. Par exemple le schéma décentré amont d'ordre 1:
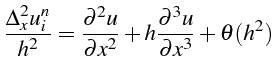
peut conduire à un schéma à l'ordre 2:
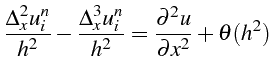
Le tableau ci-dessous donne quelques une de ces relations :
| Dérivée | opér. D.F. | approximation DF | ordre
|
|---|
La discrétisation des dérivées en temps procède de la même démarche.
En utilisant des développements de Taylor en temps de
![]() au voisinage de
au voisinage de
![]() , on obtiens les formules classiques:
, on obtiens les formules classiques:
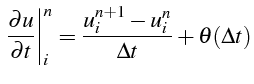
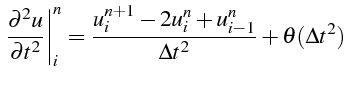
Le tableau ci dessous donne les approximations classiques des dérivées en temps
| Dérivée | opérateur D.F. | approximation DF | ordre
|
|---|