suivant: 2.7 Analyse de Fourier monter: 2. Construction de schéma précédent: 2.5 Equations discrétes et Table des matières
Ayant construit une équation discréte
![]() ,
il faut ensuite s'assurer que la solution approchée
,
il faut ensuite s'assurer que la solution approchée
![]() converge
vers la solution exacte
converge
vers la solution exacte
![]() lorsque les paramètres de discrétisations
lorsque les paramètres de discrétisations
![]() (pas en temps
(pas en temps
![]() , pas en espace
, pas en espace
![]() ) tendent
vers zéro indépendamment!
) tendent
vers zéro indépendamment!
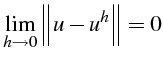
L'étude directe de l'erreur
![]() peut être très compliqué et
pas toujours possible. On va donc étudier d'autres propriétés de la
discrétisation, qui vont permettre de conclure plus facilement.
peut être très compliqué et
pas toujours possible. On va donc étudier d'autres propriétés de la
discrétisation, qui vont permettre de conclure plus facilement.
La consistance caractérise la façon dont l'équation aux différences
finies EDF (
![]() ) approche l'équation
aux dérivées partielles EDP (
) approche l'équation
aux dérivées partielles EDP (
![]() ).
).
![\bgroup\color{black}$\displaystyle E_{t}=\mathcal{L}^{h}[u_{ex}(i\Delta x)]-f^{h}-\mathcal{L}[u_{ex}]_{(i\Delta x)}-f_{(i\Delta x)}$\egroup](img897.png)
ce qui donne, compte tenu du fait que
![]() et
que
et
que
![]() (la valeur de
(la valeur de
![]() est la valeur nodale
du second membre
est la valeur nodale
du second membre
![]() )
)
![\bgroup\color{black}$\displaystyle E_{t}=\mathcal{L}^{h}[u_{ex}(i\Delta x)]-f^{h}$\egroup](img901.png)
Cette différence est l'erreur de troncature du schéma aux différences
finies, et corresponds donc à l'erreur commise lorsque l'on remplace
la solution approchée
![]() par la solution exacte
par la solution exacte
![]() aux
noeuds du maillage
aux
noeuds du maillage
![]() dans l'équation aux différences
EDF.
dans l'équation aux différences
EDF.
|
![$\displaystyle \lim_{h\rightarrow0}E_{t}=\mathcal{L}^{h}[u_{ex}(i\Delta x)]-f^{h}=0$](img903.png)
|
Pour calculer cette erreur de troncature, on développe la solution
exacte
![]() en série de Taylor autour de sa valeur aux noeuds,
et on l'exprime en fonction des pas de discrétisation
en série de Taylor autour de sa valeur aux noeuds,
et on l'exprime en fonction des pas de discrétisation
![]() . Le schéma
est alors consistant si cette erreur se comporte comme
. Le schéma
est alors consistant si cette erreur se comporte comme
![]() (avec
(avec
![]() ). Cette erreur de tronacture nous fournit aussi la précision
du schéma.
). Cette erreur de tronacture nous fournit aussi la précision
du schéma.
|
|
Si le schéma dépend de plusieurs paramêtres (pas en temps
![]() et pas en espace
et pas en espace
![]() ), on exprime bien entendu l'erreur de
troncature en fonction de ces paramêtres:
), on exprime bien entendu l'erreur de
troncature en fonction de ces paramêtres:
La précision est alors d'ordre
![]() en espace et d'ordre
en espace et d'ordre
![]() en temps.
en temps.
La notion de stabilité ne s'applique qu'au cas de la discrétisation d'un problème dépendant du temps (problème parabolique ou hyperbolique). Elle s'applique donc à des schèmas, pour lesquels on calcule des solutions de façon itérative. Les calculs s'éffectuent sur des ordinateurs avec une précision finie, et donc sont sujet à des erreurs d'arrondis. Lors d'un calcul itératif, ces erreurs peuvent être amplifiées par le schèma numérique. Le but de l'étude de stabilité est donc de déterminer quelle est l'amplification des erreurs (ou perturbations) par le schèma.
|
|
Soit
![]() la solution à l'étape
la solution à l'étape
![]() et
et
![]() la
solution à l'étape
la
solution à l'étape
![]() , l'équation aux différences (
, l'équation aux différences (
![]() )
s'écrit dans ce cas :
)
s'écrit dans ce cas :
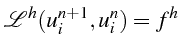
Soit
![]() une perturbation de la solution à l'étape
une perturbation de la solution à l'étape
![]() . La solution perturbée
. La solution perturbée
![]() à l'étape
à l'étape
![]() est solution de l'équation aux différences:
est solution de l'équation aux différences:
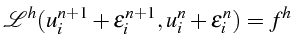
L'équation sur la perturbation est obtenue en effectuant la différence
de ces 2 équations, et si le problème est linéaire, on obtiens
l'évolution de la perturbation
![]() :
:
On décompose cette perturbation en tout point
![]() du
maillage et à tout instant
du
maillage et à tout instant
![]() sous la forme d'une série de modes
de Fourier (en notant
sous la forme d'une série de modes
de Fourier (en notant
![]() ):
):
Le problème étant supposé linéaire, chacun des modes vérifie l'équation
(2.53), qui s'écrit pour un mode
![]() :
:
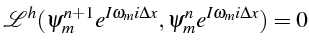
De cette équation, il faut calculer le rapport d'amplification de
l'amplitude du mode
![]()
![]() en
fonction des paramêtres
en
fonction des paramêtres
![]() et
et
![]() . Le schéma est
dit stable si les perturbations ne sont pas amplifiées.
. Le schéma est
dit stable si les perturbations ne sont pas amplifiées.
Il faut donc déterminer à quelles conditions sur les paramêtres
![]() et
et
![]() ce rapport reste en module inférieure à 1 pour tous
les modes (i.e.
ce rapport reste en module inférieure à 1 pour tous
les modes (i.e.
![]() ).
).
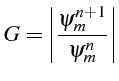
On utilise un résultat d'analyse du à Lax (Richtmyer et Norton 1967):
|
|
La consistance et la stabilité d'un schéma sont en général beaucoup plus facile à étudier que sa convergence.
Dans ce cas, seule la consistance est nécessaire pour assurer la convergence.