suivant: 3. Étude de schémas monter: 2. Construction de schéma précédent: 2.6 Convergence Table des matières
L'analyse de Fourier permet une étude des propriétés d'un schéma aux différences finies, en particulier dans le cadre une équation parabolique, comme l'équation de convection diffusion:
On cherche une solution sous la forme d'une serie de Fourier en espace
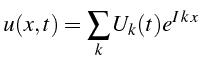
![]() est le nombre d'onde:
est le nombre d'onde:
![]() (où
(où
![]() est
la longueur d'onde)
est
la longueur d'onde)
L'équation d'évolution du mode de Fourier
![]() s'écrit:
s'écrit:
Cette équation s'intégre entre
![]() et
et
![]() , en supposant
, en supposant
![]() et
et
![]() constant sur l'intervalle de temps:
constant sur l'intervalle de temps:
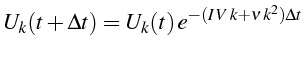
On peut donc écrire la relation entre le mode de Fourier
![]() à l'instant
à l'instant
![]() et
et
![]() :
:
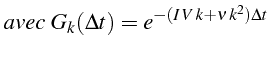
![]() est appelé le symbol de l'opérateur (ou
équation) (2.55).
est appelé le symbol de l'opérateur (ou
équation) (2.55).
Ce symbol s'écrit sous la forme générale
et permet de calculer la solution à l'étape
![]() en fonction
de la solution à l'étape
en fonction
de la solution à l'étape
![]()
Si on cherche la solution de (2.55) sous la forme d'une onde progressive:
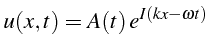 soit
soit 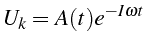
pour un symbol
![]() donnée par la relation (2.57), on
en déduit
donnée par la relation (2.57), on
en déduit
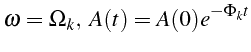
L'onde est donc une onde progressive qui se propage avec une vitesse
![]() et qui se trouve amortie exponentiellement:
et qui se trouve amortie exponentiellement:
englishANIMATION onde progressive
Pour analyser le schéma D.F., on éffectue la transformée de Fourier
des valeurs
![]() dans l'équation aux différences:
dans l'équation aux différences:
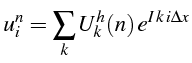
d'où l'on déduit une relation pour le mode
![]()
![]() est appelée le symbol du schéma D.F.
(équivalent discret de
est appelée le symbol du schéma D.F.
(équivalent discret de
![]() ).
).
Ce symbol
![]() peut sécrire sous la forme
peut sécrire sous la forme
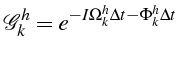
avec
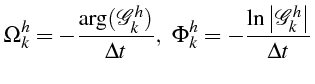
Si le schéma D.F. approchait exactement l'équation, on aurait
![]() ,
ce qui n'est évidemment pas le cas. On définit donc
,
ce qui n'est évidemment pas le cas. On définit donc
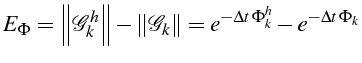
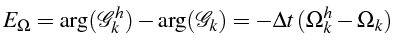
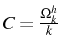 et avec
un amortissement exponentielle de coefficient
et avec
un amortissement exponentielle de coefficient
Si à l'instant
![]() , la solution approchée coincide avec la solution
exacte. A l'instant
, la solution approchée coincide avec la solution
exacte. A l'instant
![]() , l'onde calculée aura subi un déphase
, l'onde calculée aura subi un déphase
![]() par rapport à la solution exacte, ainsi qu'un amortissement
de
par rapport à la solution exacte, ainsi qu'un amortissement
de
![]() par rapport à cette même onde. La solution calculée
sera donc en retard par rapport à la solution exacte si
par rapport à cette même onde. La solution calculée
sera donc en retard par rapport à la solution exacte si
![]() est positif, et en avance sinon.
est positif, et en avance sinon.
On note aussi, que la relation d'ondes (2.58) est aussi valable
pour une perturbation
![]() ,
et fournit donc l'évolution de l'amplitude et la phase des perturbations:
,
et fournit donc l'évolution de l'amplitude et la phase des perturbations:
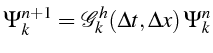
Le module du symbol
![]() de l'équation D.F. est
donc le facteur d'amplification du schéma
de l'équation D.F. est
donc le facteur d'amplification du schéma
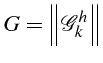
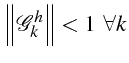
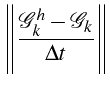 |
Une approximation D.F. de l'équation de convection-diffusion (2.55) est le schéma D.F. centré suivant:
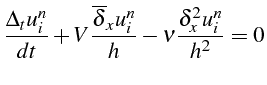
soit
On introduit les 2 nombres sans dimensions suivants:
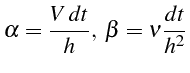
Le symbol du schéma s'écrit:
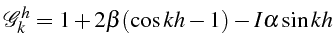
Son module s'écrit en fonction de
![]() :
:
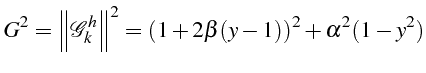
C'est un polynôme de degré 2 en
![]() que l'on étudie entre
que l'on étudie entre
![]() où il est positif. Il vérifie:
où il est positif. Il vérifie:
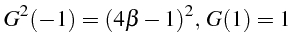
Sa dérivée s'écrit:
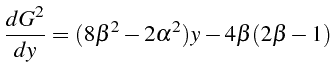
et vaut en
![]()
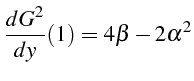
Pour que
![]() pour
pour
![]() , il est donc suffisant que:
, il est donc suffisant que:
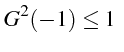 et
et 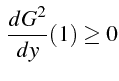
soit
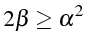 et
et
La condition de stabilité conduit à
On retrouve la condition de stabilité pour l'équation de la chaleur:
avec une condition supplémentaire sur le pas en temps
![]() :
:
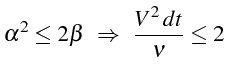
que l'on peut écrire en fonction du nombre de Courant
![]() et
d'un nombre de Pechlet
et
d'un nombre de Pechlet
![]() :
:
En posant
![]() on peut calculer un développement en série
de Taylor de
on peut calculer un développement en série
de Taylor de
![]() en
en
![]() :
:
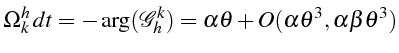
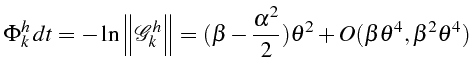
soit en fonction de
![]() et
et
![]() :
:
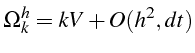
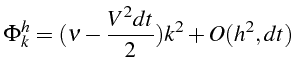
d'où l'expression de
![]()
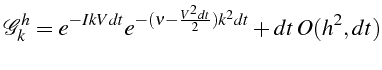
Le schéma est donc consistant et d'ordre
![]() puisque:
puisque:
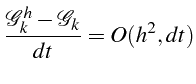
L solution approchée d'onde progressive se déplace (pour les petits
nombres d'ondes
![]() , i.e. pour
, i.e. pour
![]() petit) avec une célérité
petit) avec une célérité
![]() et est amortie avec une coefficient
et est amortie avec une coefficient
![]() ,
qui doit donc être positif. On retrouve ainsi une des conditions de
stabilité (2.62):
,
qui doit donc être positif. On retrouve ainsi une des conditions de
stabilité (2.62):
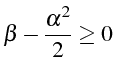
Si la solution exacte vérifie un principe du maximum:
![\bgroup\color{black}$\displaystyle \min_{x\in[a,b]}u(x,t^{n})\leq u(x,t^{n+1})\leq\max_{x\in[a,b]}u(x,t^{n})$\egroup](img1009.png)
on souhaite que la solution approchée
![]() vérifie un principe
identique. Pour cela on peut imposer au schéma aux D.F. d'être positif.
vérifie un principe
identique. Pour cela on peut imposer au schéma aux D.F. d'être positif.
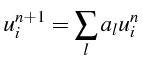
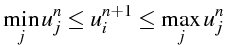
et est donc
![]() décroissante (
décroissante (
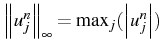 :
:
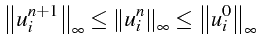
La condition de positivité pour le schéma (2.59) s'écrit:
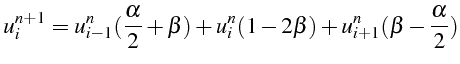
ce qui implique:
Cette condition impose donc les 2 relations suivantes:
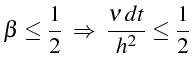
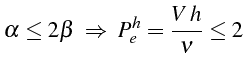
La condition
est plus restrictive que la condition de stabilité (2.60), et c'est donc celle que l'on retiendra pour éviter les oscillations dans la solution.
Cette relation impose:
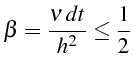
et une condition sur le nombre de Pechlet
Avec la condition (2.61), cette dernière condition vérifie la condition de stabilite (2.61)+(2.62), puisqu'elle impose:
et donc la condition (2.61)+(2.62):
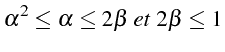
C'est donc les conditions (2.61)+(2.64) que l'on retiendra pour éviter les oscillations dans la solution:
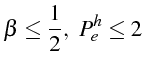
On note que si
![]() , on a
, on a
![]() et le schéma D.F. explicite
centré est inconditionnellement instable.
et le schéma D.F. explicite
centré est inconditionnellement instable.
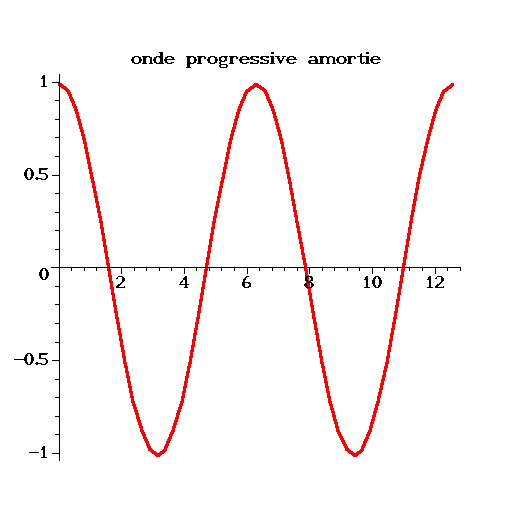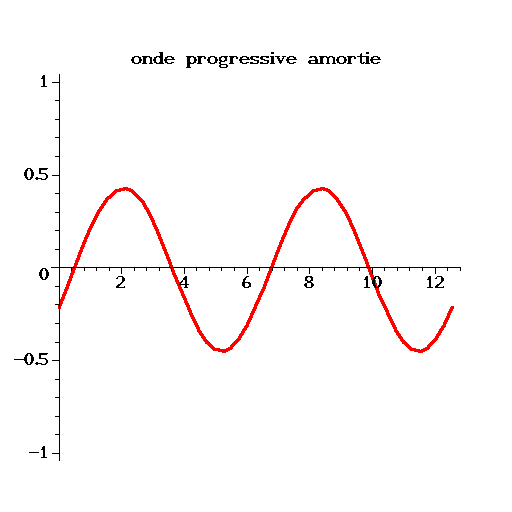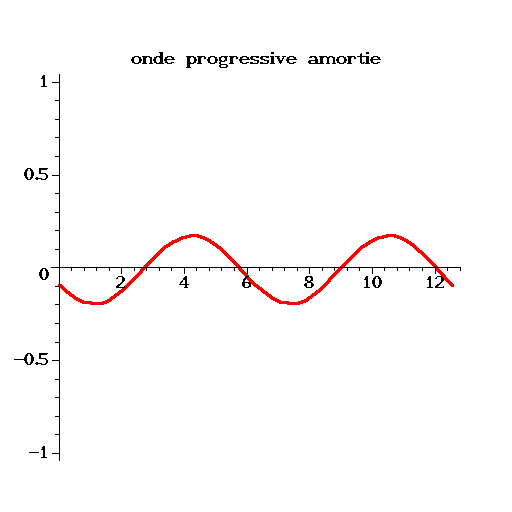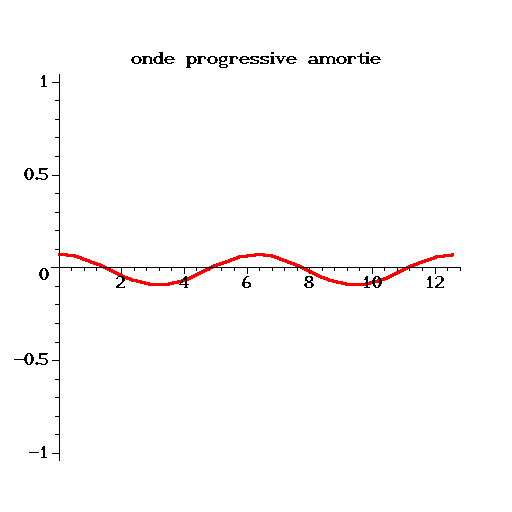
On a calculé avec Matlab la solution approchée pour une condition initiale
et des conditions aux limites périodiques.
La solution exacte est alors une onde progressive amortie:
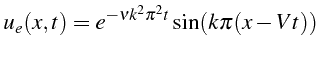
Sur un maillage de
![]() avec
avec
![]() , pour le mode
, pour le mode
![]() et
et
![]() , on a réalisé différentes simulations pour différentes
valeurs de
, on a réalisé différentes simulations pour différentes
valeurs de
![]() , i.e. du nombre de Pechlet
, i.e. du nombre de Pechlet
![]() .
.
On constate sur la figure (2.2), que pour des faibles valeurs
de
![]() , la solution numérique approche très bien la solution
exacte. L'erreur augmente quand le nombre de Pechlet augmente, la
solution numérique étant beaucoup moins diffusive que la solution
exacte. On remarque même que pour
, la solution numérique approche très bien la solution
exacte. L'erreur augmente quand le nombre de Pechlet augmente, la
solution numérique étant beaucoup moins diffusive que la solution
exacte. On remarque même que pour
![]() , qui est la limite
de stabilité (i.e.
, qui est la limite
de stabilité (i.e.
![]() ), la solution numérique ne
diffuse plus (
), la solution numérique ne
diffuse plus (
![]() ).
).
Ce schéma est donc utilisable uniqument pour des problèmes peu convectifs !
englishANIMATION schéma explicite centré