5.3 Applications: mouvement gyroscopique

On étudie une toupie de masse m, en rotation autour son axe principal d'inertie (axe de révolution) $\overrightarrow{OG}=l\,\overrightarrow{Z_{2}}$. On suppose que le point O est immobile et la liaison sans frottement.

Les 3 degrés de liberté du système sont les 3 angles d'Euler:

1. $\theta$ l'angle de précession de l'axe de la toupie autour de $Z_{0}$
2. $\phi$ l'angle de nutation (oscillation de l'axe autour de $Y_{1}$)
3. $\psi$ l'angle de rotation propre de la toupie autour de son axe $Z_{2}$

La toupie est soumise aux forces suivantes:

1. la force de gravité $-mg\overrightarrow{Z_{0}}$ en G
2. la réaction $\overrightarrow{R}$ en O

L'application du théorème du moment cinétique en O permet d'obtenir les 3 équations du mouvement en $\theta,\phi,\psi$, en éliminant l'inconnue de tension (qui est obtenue par application du théorème sur la quantité de mouvement).

$$\frac{d}{dt}\overrightarrow{\sigma}(O)=-mgl\,\sin\phi\overrightarrow{Y_{1}}$$

5.3.1 Effet gyroscopique

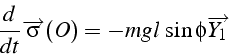
Si à l'instant initial, la toupie tourne rapidement autour de son axe $Z_{2}$ avec une vitesse angulaire $\omega=\dot{\psi}$, le moment cinétique vaut approximativement $\overrightarrow{\sigma}(O)\approx I\omega\overrightarrow{Z_{2}}$ (où $I$ est le moment d'inertie autour de l'axe $Z_{2}$). Le moment du poids engendre un couple suivant $\overrightarrow{Y_{1}}$ perpendiculaire à $\overrightarrow{\sigma}(O)$, qui force l'axe de rotation propre $Z_{2}$ à tourner autour d'un axe perpendiculaire à $Y_{1}$, $Z_{2}$ (effet gyroscopique). Si $\phi\approx\pi/2$ , alors la rotation s'effectue suivant $Z_{0}$ avec un mouvement lent de précession $\Omega=\dot{\theta}\approx cste$.

En effet l'équation du mouvement (théorème du moment cinétique) s'écrit:

$$\frac{d}{dt}\overrightarrow{\sigma}(O)=\mathcal{M}_{O}(P)=l\overrightarrow{Z_{2}}\wedge-mg\overrightarrow{Z_{0}}$$

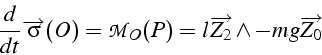
avec $\overrightarrow{\sigma}(O)\approx I\omega\overrightarrow{Z_{2}}$. D'où l'on déduit, si $\omega$ est très grand que:

$$\frac{d}{dt}\overrightarrow{\sigma}(O)=\Omega\overrightarrow{Z_{0}}\wedge\overrightarrow{\sigma}(O)$$

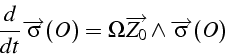
Le moment cinétique $\overrightarrow{\sigma}(O)$, et donc la toupie se met à tourner autour de l'axe vertical $\overrightarrow{Z_{0}}$ avec une vitesse de rotation $\Omega$ (effet gyroscopique). Ce mouvement est appelé précession. La vitesse angulaire de la précession $\Omega$ est donnée par :

$$\Omega=-\frac{mgl}{I\omega}$$

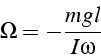
et est d'autant plus petite que $\omega$ est grand.

La précession peut être démontrée en plaçant un gyroscope tournant sur son axe horizontal et supporté lâchement à une extrémité. Au lieu de tomber comme on peut s'y attendre, le gyroscope apparaıt comme défiant la gravité en restant sur son axe horizontal, même si un bout de l'axe n'est pas supporté. L'extrémité libre de l'axe décrit lentement un cercle dans un plan horizontal. Le moment du gyroscope est fourni par un couple de forces : la gravité pousse vers le bas le centre de la masse du dispositif, et la réaction en O le pousse vers le haut pour supporter le côté libre. Le déplacement résultant de ce moment n'est pas vers le bas, comme l'intuition nous le fait supposer, mais perpendiculaire à la fois au mouvement gravitationnel (le bas) et l'axe de rotation (vers l'extérieur du point d'appui), c'est-à-dire dans une direction horizontale vers l'avant, faisant faire à l'appareil une rotation lente autour du point de support. La réaction en O possède donc une composante horizontale (et non pas uniquement vertical), qui génère ce déplacement .

La démonstration la plus simple et la plus parlante consiste à tenir à bout de bras une roue de vélo par les écrous du moyeu et de la faire tourner rapidement par une autre personne. Lorsque l'on tente de pencher sur le côté la roue en rotation, on verra que le mouvement sera décalé de 90^ !

5.3.2 Cas général

Dans le cas générale, on a un mouvement beaucoup plus compliqué avec un mouvement de précession et de nutation de l'axe de la toupie, et des vitesses angulaires variants au cours du temps.

On note cependant que certaines quantités se conservent au cours du temps:

1. l'énergie totale = énergie cinétique + énergie potentielle
   
   
   $$E=E_{c}+U=cste$$
   
   

2. la projection du moment cinétique suivant $\overrightarrow{Z_{2}}$ (passe par G) et suivant $\overrightarrow{Z_{0}}$ (direction du poids), puisque que le moment du poids est perpendiculaire à ces deux directions.
   
   
   $$\overrightarrow{\sigma}(O).\overrightarrow{Z_{2}}=cste,\,\,\,\,\,\overrightarrow{\sigma}(O).\overrightarrow{Z_{0}}=cste$$
   
   

Ce sont les 3 intégrales premières du mouvement.

5.3.3 Objectif de l'étude

On se propose d'étudier avec Maple le mouvement de la toupie dans le cas général, en retrouvant les propriétés décrites ci dessus.