suivant: 5.5 Programme Maple monter: 5. Dynamique du solide précédent: 5.3 Applications: mouvement gyroscopique Table des matières
On définit 3 repères:
![\includegraphics[width=0.3\textwidth]{CHAP4/toupie}](img206.png)
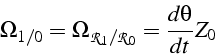
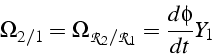
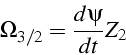
![\begin{displaymath}
\mathcal{M}_{0/1}=\left[\begin{array}{ccc}
\cos\theta & -\si...
...end{array}\right],\,\,\,\mathcal{M}_{1/0}=\mathcal{M}_{0/1}^{t}\end{displaymath}](img213.png)
![\begin{displaymath}
\mathcal{M}_{1/2}=\left[\begin{array}{ccc}
\cos\phi & 0 & \s...
...end{array}\right],\,\,\,\mathcal{M}_{2/1}=\mathcal{M}_{1/2}^{t}\end{displaymath}](img214.png)
Les équations sont projetés dans
![]() . Le vecteur instantané
de rotation s'écrit dans
. Le vecteur instantané
de rotation s'écrit dans
![]() :
:
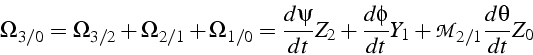
La toupie est un solide de révolution d'axe ![]() , donc dans
, donc dans
![]() la matrice d'inertie est diagonale et vaut:
la matrice d'inertie est diagonale et vaut:
![\begin{displaymath}
\mathcal{I}_{G}=\left[\begin{array}{ccc}
I_{2} & 0 & 0\\
0 & I_{2} & 0\\
0 & 0 & I_{1}\end{array}\right]\end{displaymath}](img216.png)
d'où le moment cinétique en ![]() dans
dans
![]()
puis en ![]() en fonction de la vitesse
en fonction de la vitesse ![]() en
en ![]() :
:
On fait alors apparaıtre le moment d'inertie en O
Le moment du poids dans
![]() s'écrit
s'écrit
d'où l'équation du mouvement dans
![]()
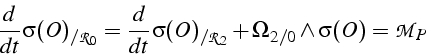
qui fournit les 3 équations différentielles du second ordre du problème.
En notant que la troisième équation (projection suivant ![]() )
traduit la conservation du moment cinétique suivant
)
traduit la conservation du moment cinétique suivant ![]() :
:
on peut simplifier les 2 autres équations
En combinant ces équations on doit retrouver les 3 intégrales premières du mouvement:
On se place dans le cas d'une toupie constituée d'un disque de rayon
![]() sur un axe de longueur
sur un axe de longueur ![]() , avec
, avec ![]()
On se place tout d'abord dans le cas ![]() pour retrouver
la solution particulière de précession
pour retrouver
la solution particulière de précession
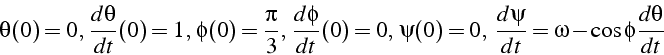
i.e., on lance la toupie avec un léger mouvement de rotation autour
de ![]() avec un axe incliné de
avec un axe incliné de ![]() par rapport à la vertical
par rapport à la vertical
![]() . On étudie les 5 cas suivants:
. On étudie les 5 cas suivants: