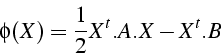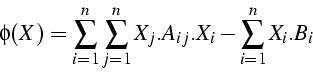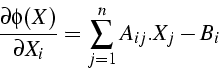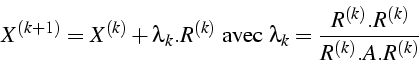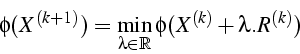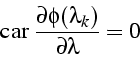Sous-sections
- A est une matrice symétrique définie positive si
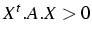 si
si 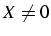 i.e.
i.e. 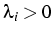
- soit la forme quadratique définie positive
- Le minimum de
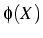 est solution de
est solution de 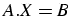
X = Arg Min(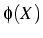 )
)
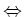
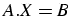
- itération de Gradient = minimisation de
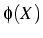
suite 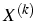 tq
tq
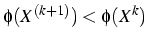
- théorème:
- Si A est une matrice à symétrique définie positive,
alors la méthode de gradient converge
d'ou la convergence de l'algorithme de gradient
- variante de l'algorithme: algorithme de "gradients conjugués"
Pr. Marc BUFFAT
marc.buffat@univ-lyon1.fr
2007-11-26