suivant: 5.6 Méthode de Gradient monter: 5. Méthodes itératives de précédent: 5.4 Méthode de Gauss-Seidel Table des matières
La méthode SOR est une accélération des méthodes de Gauss-Seidel (ou
Jacobi). La solution ![]() est une combinaison linéaire de
la solution Gauss-Seidel
est une combinaison linéaire de
la solution Gauss-Seidel ![]() et de la solution à l'itération
précédente
et de la solution à l'itération
précédente ![]() , avec un paramêtre
, avec un paramêtre ![]() t.q.
t.q. ![]()
La suite itérative s'écrit alors:
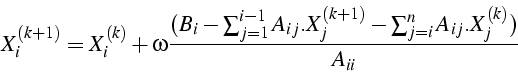
Attention: le paramêtre ![]() optimal dépend de la matrice
optimal dépend de la matrice ![]() !
!