Sous-sections
- décomposition de A :
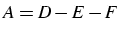
- D : diagonale de A
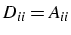 et
et 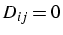 si
si 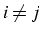
- E : matrice triangulaire inférieure
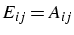 si
si 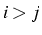 et
et 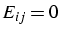 si
si 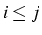
- F : matrice triangulaire supérieure
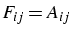 si
si 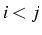 et
et 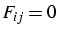 si
si 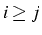
- itération
- de Jacobi
- théorème:
- Si A est une matrice à diagonale dominante, alors la
méthode de Jacobi converge
- définition:
- matrice à diagonale dominante
A est à diagonale dominante si
- demonstration:
- matrice de l' itération
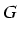
- Algorithme
- 8
![\begin{algorithm}
% latex2html id marker 1071\par
\caption{jacobi
}
\par
\begi...
...i]
\par
finpour
\par
jusqu'à sqrt(Residu) $<$ Eps\end{list}\par
\end{algorithm}](img267.png)
Pr. Marc BUFFAT
marc.buffat@univ-lyon1.fr
2007-11-26
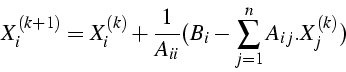
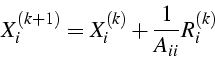
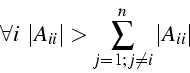
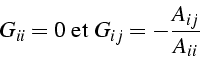
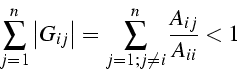
![\begin{algorithm}
% latex2html id marker 1071\par
\caption{jacobi
}
\par
\begi...
...i]
\par
finpour
\par
jusqu'à sqrt(Residu) $<$ Eps\end{list}\par
\end{algorithm}](img267.png)