suivant: 5.3 Equations différentielles monter: 5. Annexe: EDP et précédent: 5.1 Equations aux dérivées Table des matières
Soit l'équation aux dérivées partielles
![]() est la fonction inconnue. Les coefficients
est la fonction inconnue. Les coefficients
![]() ,
,
![]() et
et
![]() dépendent de
dépendent de
![]() et
et
![]() ; le coefficient
; le coefficient
![]() dépend de
dépend de
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Posons de manière classique:
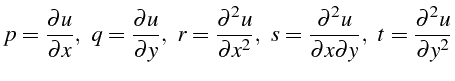
et soit
![]() une courbe du domaine
une courbe du domaine
![]() .
.
Le long de
![]() , on a les relations suivantes:
, on a les relations suivantes:
En éliminant
![]() et
et
![]() dans (4.65) en utilisant (4.63)
et (4.64), il vient:
dans (4.65) en utilisant (4.63)
et (4.64), il vient:
Si
![]() , pente de la courbe
, pente de la courbe
![]() , vérifie:
, vérifie:
l'équation (4.66) se réduit à une simple relation entre
![]() et
et
![]()
Le long d'une courbe
![]() de pente
de pente
![]() racine de
(4.67), appelée “courbe caractéristique”, les dérivées
racine de
(4.67), appelée “courbe caractéristique”, les dérivées
![]() et
et
![]() de la solution de l'équation aux dérivées partielles
(4.62) sont liées par la relation (4.68), dite “relation
caractéristique”.
de la solution de l'équation aux dérivées partielles
(4.62) sont liées par la relation (4.68), dite “relation
caractéristique”.
Les deux racines de (4.67) définissent les directions caractéristiques de l'équation aux dérivées partielles (4.62):
Soit l'équation aux dérivées partielles (4.62), supposons
que sur une courbe
![]() de
de
![]() on connait la fonction
on connait la fonction
![]() et sa dérivée normale
et sa dérivée normale
![]() .
.
Peut on construire dans un voisinage de
![]() la solution
la solution
![]() de (4.62)?
de (4.62)?
![\includegraphics[width=0.5\paperwidth]{CHAP0/edp2}](img2293.png)
Pour cela, il est nécéssaire de pouvoir calculer toutes les dérivées
partielles successives de
![]() sur
sur
![]() (sous réserve de la régularité
de la solution) pour construire le développement en série de Taylor.
Soit
(sous réserve de la régularité
de la solution) pour construire le développement en série de Taylor.
Soit
![]() un point de
un point de
![]() de coordonnées
de coordonnées
![]() , au voisinage
de
, au voisinage
de
![]() la solution
la solution
![]() s'écrit:
s'écrit:
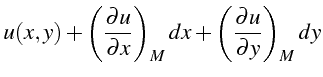 |
|||
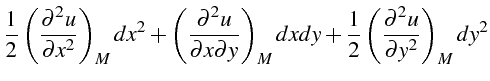 |
|||
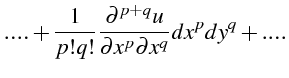 |
Par hypothèse, on connait
![]() sur
sur
![]() , donc
, donc
![]() et
sa dérivée le long de
et
sa dérivée le long de
![]() :
:
![]() , ainsi que
sa dérivée normale
, ainsi que
sa dérivée normale
![]() (on a noté
(on a noté
![]() l'abscisse
curviligne le long de
l'abscisse
curviligne le long de
![]() ).
).
Par changement de repère, on en déduit les 2 dérivées premières de
![]() en résolvant le système linéaire:
en résolvant le système linéaire:
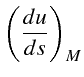 |
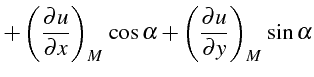 |
||
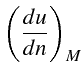 |
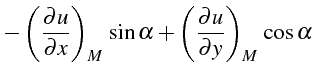 |
On a noté
![]() l'angle polaire de la tangente unitaire
l'angle polaire de la tangente unitaire
![]() à
à
![]() :
:
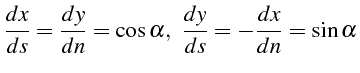
Pour calculer les 3 dérivées secondes de
![]() , on
, on