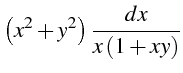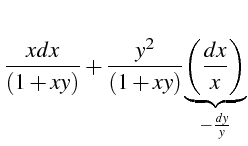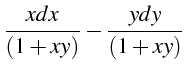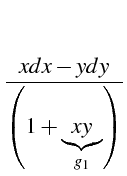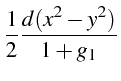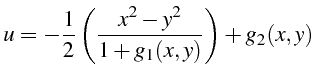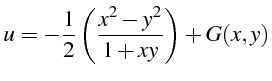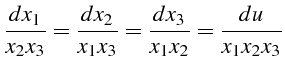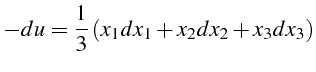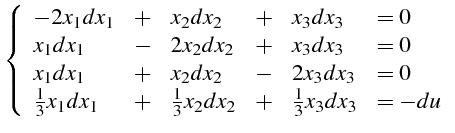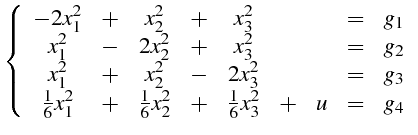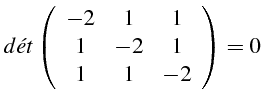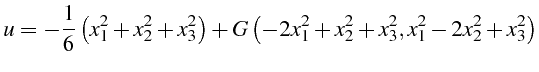Sous-sections
- Equation différentielle d'ordre n:
- Soit
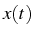 une fonction
inconnue de la variable
une fonction
inconnue de la variable . On désigne par :
. On désigne par :
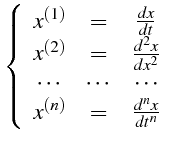 |
(5.17) |
les 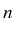 premières dérivées de cette fonction. On appelle Equation
différentielle d'ordre
premières dérivées de cette fonction. On appelle Equation
différentielle d'ordre 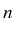 , l'équation :
, l'équation :
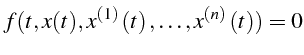 |
(5.18) |
reliant les variables
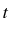 ,
,
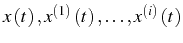 avec
avec
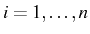 .
.
- Système différentielle d'ordre n:
- On appelle système différentiel
un ensemble d'équations reliant la variable
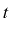 , un certain nombre
de fonctions et certaines de leurs dérivées:
, un certain nombre
de fonctions et certaines de leurs dérivées:
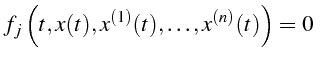 pour pour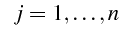 |
(5.19) |
En particulier, une équation unique du type (4.70) peut être
écrite sous forme d'un système différentiel. En effet, si on pose
:
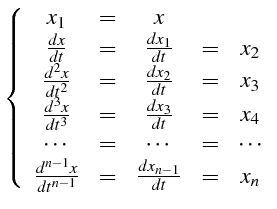 |
(5.20) |
L'équation (4.70) prend la forme :
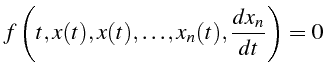 |
(5.21) |
et l'équation (4.70) est équivalente au système :
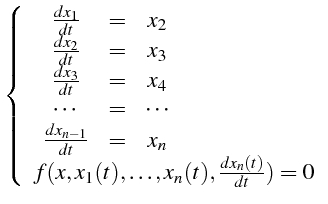 |
(5.22) |
Le système s'écrit sous la forme :
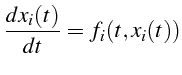 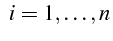 |
(5.23) |
qui est dite forme canonique.
Soit le système canonique écrit sous la forme vectorielle
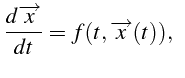 avec avec 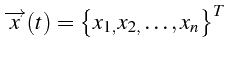 |
(5.24) |
Le problème de Cauchy consiste à trouver la solution
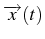 du système qui pour
du système qui pour
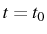 passe par le point donné
passe par le point donné
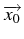 de coordonnées
de coordonnées
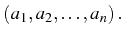 La solution
s'écrit alors sous la forme :
La solution
s'écrit alors sous la forme :
Si la solution est unique au voisinage de
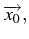 le point correspondant à
le point correspondant à
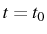 est dit régulier.
est dit régulier.
A chaque point régulier correspond une solution du système dépendant
des
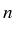 coordonnées
coordonnées
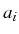 du point considéré. On l'appelle solution
générale du système.
du point considéré. On l'appelle solution
générale du système.
- condition de Lipschitz:
- On dit que la fonction vectorielle
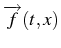 à valeurs dans
à valeurs dans 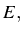 vérifie une condition
de Lipschitz, si quelque soit
vérifie une condition
de Lipschitz, si quelque soit 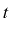
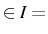 (intervalle de temps) et
pour tout couple
(intervalle de temps) et
pour tout couple
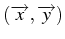 de vecteurs
de vecteurs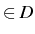 , nous avons l'inégalité suivante :
, nous avons l'inégalité suivante :
ou 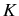 est une constante indépendante de
est une constante indépendante de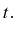
Théorème: Théorème de Cauchy.
Soit
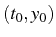 un point de
un point de
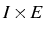 (où I est
un intervalle de temps). Si
(où I est
un intervalle de temps). Si
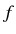 est localement Lipschitzienne sur
est localement Lipschitzienne sur
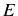 et continue, le problème de Cauchy associé au point
et continue, le problème de Cauchy associé au point
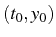 admet une solution unique.
admet une solution unique.
Etude au voisinage d'un point régulier relatif au système différentiel
canonique:
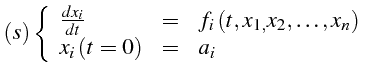 |
(5.29) |
(où
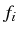 vérifie les conditions de Cauchy, car point régulier)
vérifie les conditions de Cauchy, car point régulier)
La solution de
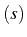 correspond à un point
correspond à un point
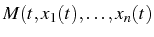 )
et décrit une courbe intégrale du système
)
et décrit une courbe intégrale du système
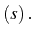
Par intégration,
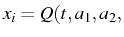 ...,
...,
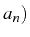 ou
encore
ou
encore
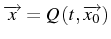 avec
avec
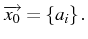 Inversement,
on peut écrire (par inversion de la relation précédente)
Inversement,
on peut écrire (par inversion de la relation précédente)
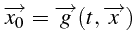 |
(5.30) |
Le long de
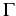 (courbe intégrale), la fonction
(courbe intégrale), la fonction
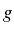 reste constante.
reste constante.
Remarque:
On ne peut pas forcément expliciter
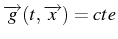 le long de
le long de
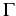 intégrale, c'est à dire, pour
intégrale, c'est à dire, pour
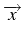 solution, nous avons
solution, nous avons
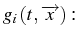
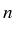 intégrales premières indépendantes. La solution de
intégrales premières indépendantes. La solution de
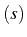 passant par
passant par
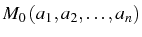 à t=t
à t=t
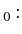
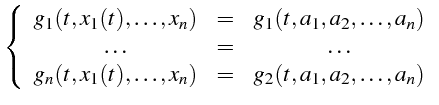 |
(5.31) |
- Intégrale première:
- On appelle intégrale première d'un système
différentiel canonique, une fonction
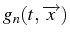 qui reste constante sur une courbe
qui reste constante sur une courbe
 intégrale.
Sa valeur sur
intégrale.
Sa valeur sur
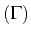 est déterminée et elle change
lorsque l'on passe de la courbe
est déterminée et elle change
lorsque l'on passe de la courbe
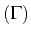 à une autre
courbe intégrale correspondant à un autre point régulier.
à une autre
courbe intégrale correspondant à un autre point régulier.
Soit
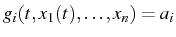 une intégrale première
le long de la courbe
une intégrale première
le long de la courbe
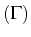 . Or le long de la courbe
. Or le long de la courbe
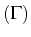 , la fonction inconnue
, la fonction inconnue
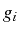 est indépendante
de
est indépendante
de
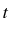 car
car
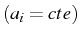 .
.
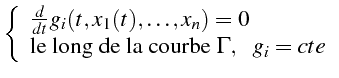 |
(5.32) |
Soit
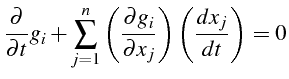 |
(5.33) |
or
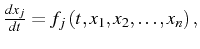 d'où
d'où
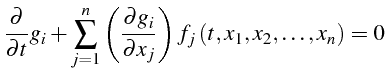 |
(5.34) |
où (4.86) est une équation aux dérivées partielles
linéaire du premier ordre.
Remarque : Si
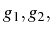 ...,
...,
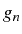 sont
sont
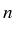 intégrales premières distinctes, toute fonction arbitraire
intégrales premières distinctes, toute fonction arbitraire
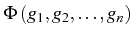 est une intégrale première.
En effet :
est une intégrale première.
En effet :
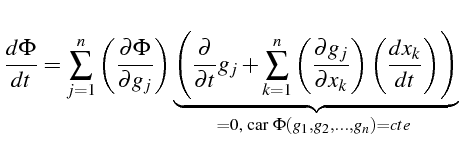 |
(5.35) |
Elle s'écrit :
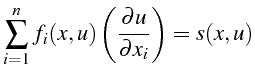 |
(5.36) |
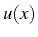 est la fonction inconnue de
est la fonction inconnue de 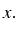
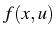 et
et 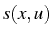 sont des fonctions connues de
sont des fonctions connues de 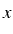 et de
et de 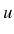 .
.
Exemple : transport d'un scalaire
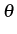 par
un champ de vitesse.
par
un champ de vitesse.
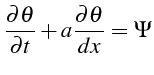 |
(5.37) |
L'équation (4.88) n'est pas linéaire :
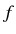 est fonction
de
est fonction
de
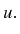
Soit
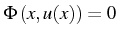 , la solution implicite de l'équation
aux dérivées partielles. Il vient en décrivant par rapport à
, la solution implicite de l'équation
aux dérivées partielles. Il vient en décrivant par rapport à
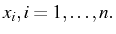
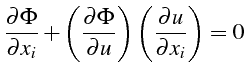 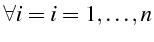 |
(5.38) |
Si l'on suppose que
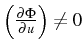 (c'est à dire que
(c'est à dire que
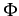 dépend bien de
dépend bien de
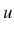 ), on obtient les expressions
des dérivées :
), on obtient les expressions
des dérivées :
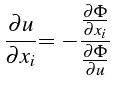 |
(5.39) |
et en remplaçant dans (4.88), on obtient :
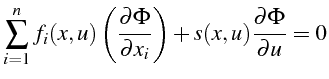 |
(5.40) |
forme linéaire associée. On voit alors que
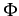 satisfait une équation
du même type que l'équation pour les intégrales premières telle que
l'équation (4.86) du système différentiel (4.75)
satisfait une équation
du même type que l'équation pour les intégrales premières telle que
l'équation (4.86) du système différentiel (4.75)
 La fonction
La fonction
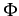 est donc elle même une intégrale première du système
différentiel canonique :
est donc elle même une intégrale première du système
différentiel canonique :
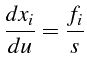 |
(5.41) |
qui peut s'écrire encore :
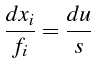  |
(5.42) |
système différentiel canonique
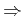 système différentiel
caractéristique.
système différentiel
caractéristique.
- Ecrire l'équation caractéristique associée,
- rechercher la famille d'intégrales premières,
- solution implicite du problème :
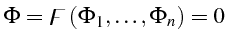 |
(5.43) |
- éventuellement en extraire une solution explicite.
Soit l'équation :
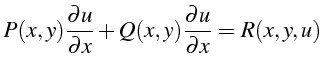 |
(5.44) |
Une solution
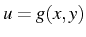 (explicite) ou
(explicite) ou
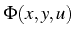 (implicite)
est dite intégrale de l'équation (4.96). On cherche une
solution implicite
(implicite)
est dite intégrale de l'équation (4.96). On cherche une
solution implicite
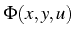 comme intégrale première du système
caractéristique :
comme intégrale première du système
caractéristique :
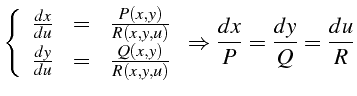 |
(5.45) |
En utilisant les égalités de l'équation (4.97) nous pouvons
écrire l'équation que vérifie
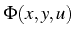 :
:
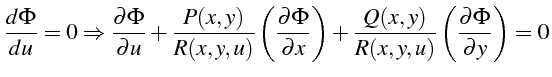 |
(5.46) |
Soit l'équation de convection mono-dimensionnelle suivante :
où
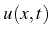 est la fonction inconnue.
est la fonction inconnue.
- Système caractéristique associé
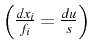 :
:
- Intégrales premières de ce système différentiel
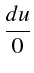 fini
fini 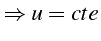
d'où
- Forme implicite de la solution
On cherche la solution générale sous la forme
- Explicite :
Cette solution est unique. A 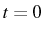 , nous avons
, nous avons
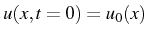
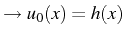 , d'où
, d'où
- Intégrer l'équation aux dérivées partielles suivantes :
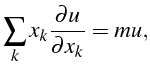 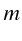 est une constante donnée est une constante donnée |
(5.47) |
- Déterminer la solution générale de
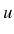 vérifiant l'équation aux dérivées
partielles suivantes :
vérifiant l'équation aux dérivées
partielles suivantes :
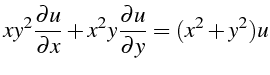 |
(5.48) |
- Intégrer l'équation aux dérivées partielles suivante :
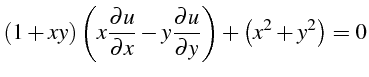 |
(5.49) |
- Trouver la solution générale de l'équation suivante
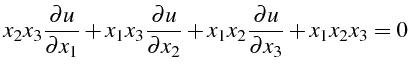 |
(5.50) |
- Le système caractéristique associé à l'équation (4.99) s'écrit
:
d'où on en déduit les intégrales premières :
La solution implicite s'écrit :
ou encore sous forme explicite :
- Le système différentiel caractéristique de l'équation (4.100)
s'écrit :
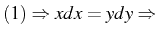
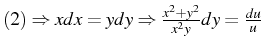
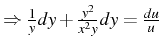 or
or
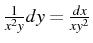 ce qui donne
ce qui donne
La solution implicite s'écrit :
ou encore
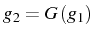 , ce qui donne
, ce qui donne
- Le système différentiel caractéristique de l'équation (4.101)
s'écrit :
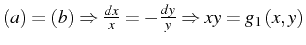
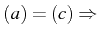
Or nous savons que le long de toute courbe solution
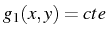 ,
par conséquent :
,
par conséquent :
Ce qui donne :
ou
- Le système différentiel s'écrit :
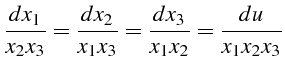 |
(5.51) |
Nous avons alors :
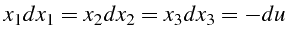 |
(5.52) |
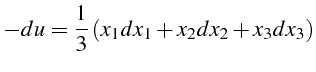 |
(5.53) |
D'où l'on déduit
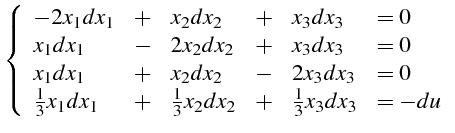 |
(5.54) |
d'où les intégrales premières :
Les trois premières intégrales premières sont dépendantes. En effet
:
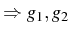 et
et 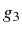 linéairement dépendantes. Nous
pouvons alors choisir comme intégrales premières
linéairement dépendantes. Nous
pouvons alors choisir comme intégrales premières
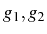 et
et
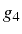 . Ceci donne
. Ceci donne
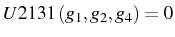 ou
encore
ou
encore
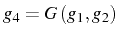 c'est à dire :
c'est à dire :
Pr. Marc BUFFAT
marc.buffat@univ-lyon1.fr
2008-04-07
![]() coordonnées
coordonnées
![]() du point considéré. On l'appelle solution
générale du système.
du point considéré. On l'appelle solution
générale du système.
![]() est continue et bornée
sur
est continue et bornée
sur ![]() , alors
, alors ![]() tq
tq
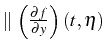
![]()
![]()
![]()
![]()
![]() vérifie les conditions de Cauchy, car point régulier)
vérifie les conditions de Cauchy, car point régulier)
![]() correspond à un point
correspond à un point
![]() )
et décrit une courbe intégrale du système
)
et décrit une courbe intégrale du système
![]()
![]() ...,
...,
![]() ou
encore
ou
encore
![]() avec
avec
![]() Inversement,
on peut écrire (par inversion de la relation précédente)
Inversement,
on peut écrire (par inversion de la relation précédente) ![]() le long de
le long de
![]() intégrale, c'est à dire, pour
intégrale, c'est à dire, pour
![]() solution, nous avons
solution, nous avons
![]()
![]() intégrales premières indépendantes. La solution de
intégrales premières indépendantes. La solution de
![]() passant par
passant par
![]() à t=t
à t=t
![]()
![]() une intégrale première
le long de la courbe
une intégrale première
le long de la courbe
![]() . Or le long de la courbe
. Or le long de la courbe
![]() , la fonction inconnue
, la fonction inconnue
![]() est indépendante
de
est indépendante
de
![]() car
car
![]() .
.![]() ...,
...,
![]() sont
sont
![]() intégrales premières distinctes, toute fonction arbitraire
intégrales premières distinctes, toute fonction arbitraire
![]() est une intégrale première.
En effet :
est une intégrale première.
En effet :![]() est fonction
de
est fonction
de
![]()
![]() , la solution implicite de l'équation
aux dérivées partielles. Il vient en décrivant par rapport à
, la solution implicite de l'équation
aux dérivées partielles. Il vient en décrivant par rapport à
![]()
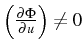 (c'est à dire que
(c'est à dire que
![]() (explicite) ou
(explicite) ou
![]() (implicite)
est dite intégrale de l'équation (4.96). On cherche une
solution implicite
(implicite)
est dite intégrale de l'équation (4.96). On cherche une
solution implicite
![]() comme intégrale première du système
caractéristique :
comme intégrale première du système
caractéristique :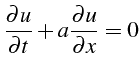
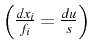 :
: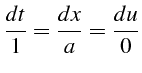
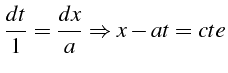
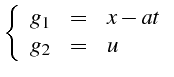
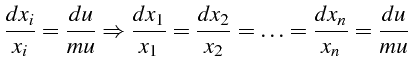
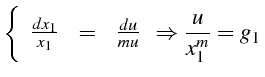
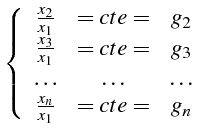
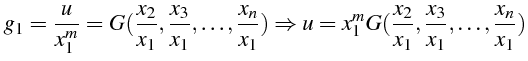
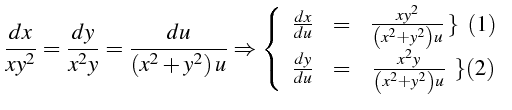
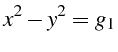
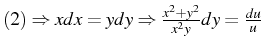
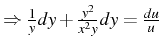 or
or
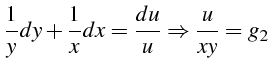
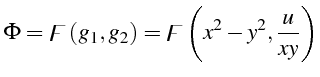
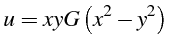
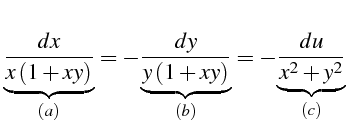
![]()