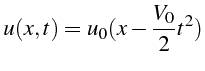suivant: 5.2 Equation aux dérivées monter: 5. Annexe: EDP et précédent: 5. Annexe: EDP et Table des matières
Il s'agit d'une équation de la forme:
où
![]() est la fonction inconnue des
est la fonction inconnue des
![]() variables
indépendantes
variables
indépendantes
![]() . Les coefficients
. Les coefficients
![]() et le second membre
et le second membre
![]() peuvent dépendre explicitement de la fonction
peuvent dépendre explicitement de la fonction
![]() . Une telle équation n'est donc pas linéaire au sens des opérateurs
puisque les
. Une telle équation n'est donc pas linéaire au sens des opérateurs
puisque les
![]() dépendent de
dépendent de
![]() et
et
![]() n'est pas forcément
linéaire en
n'est pas forcément
linéaire en
![]() . Cependant, on peut se ramener simplement au cas
linéaire en introduisant une fonction inconnue auxiliaire
. Cependant, on peut se ramener simplement au cas
linéaire en introduisant une fonction inconnue auxiliaire
![]() .
.
Supposons que la solution de l'équation (4.53) soit donnée sous la forme implicite:
Alors
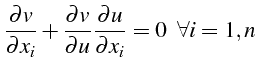
En supposant que
![]() (
(
![]() dépend
bien de
dépend
bien de
![]() ):
):
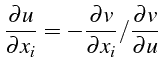
En reportant dans (4.53):
qui est une équation linéaire pour la fonction
![]() des
des
![]() variables
variables
![]() .
.
Soit le système différentielle d'ordre n et d'inconnues
![]() :
:
où
![]() est la variable inédpendante.
est la variable inédpendante.
Au point
![]() pour
pour
![]() , il passe une courbe
, il passe une courbe
![]() (unique) solution du système différentiel, dont les équations sont
de la forme:
(unique) solution du système différentiel, dont les équations sont
de la forme:
Si on résoud ces
![]() équations par rapport aux
équations par rapport aux
![]() :
:
Le long de
![]() , les fonctions
, les fonctions
![]() restent constantes. Ce
sont les “intégrales premières” du système (4.55).
restent constantes. Ce
sont les “intégrales premières” du système (4.55).
Considérons alors une fonction
![]() et déterminons
à quelle condition elle est une intégrale première de (4.55).
Sur
et déterminons
à quelle condition elle est une intégrale première de (4.55).
Sur
![]() ,
,
![]() vérifie:
vérifie:
Alors
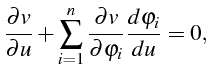 et
et 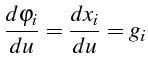
c'est à dire:
C'est l'équation des “intégrales premières” du sytème (4.55).
L'équation (4.54) sur la fonction
![]() des
des
![]() variables
variables
![]() est une équation du type (4.56). Donc
est une équation du type (4.56). Donc
![]() est une intégrale première du système différentiel
ordinaire:
est une intégrale première du système différentiel
ordinaire:
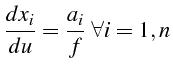
ou encore:
C'est le système différentiel caractéristique associé à (4.54).
Alors si les
![]() sont n intégrales premières distinctes,
toute fonction
sont n intégrales premières distinctes,
toute fonction
![]() est aussi une intégrale
première, c'est à dire que
est aussi une intégrale
première, c'est à dire que
![]() est constant le long d'une courbe
est constant le long d'une courbe
![]() solution du système différentiel caractéristique.
solution du système différentiel caractéristique.
Le long de
![]() ,
,
![]() soit
soit
![]() ,
qui n'est autre que la solution générale de l'équation aux dérivées
partielles (4.53) sous forme implicite.
,
qui n'est autre que la solution générale de l'équation aux dérivées
partielles (4.53) sous forme implicite.
Soit l'équation aux dérivées partielles
Le système différentiel caractéristique associé est:
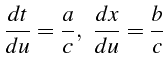
ou
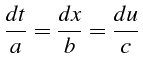
Le long de la direction caractéristique de pente
![]() ,
l'équation se réduit à:
,
l'équation se réduit à:
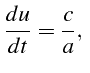 et
et 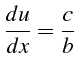
Il est possible d'intégrer l'équation (4.58) comme un système différentiel ordinaire le long d'une caractéristique, sauf si la condition initiale est fournie sur une ligne caractéristique.
Si
![]() (cas homogène),
(cas homogène),
![]() est alors constant le long des lignes
caractéristique de pente
est alors constant le long des lignes
caractéristique de pente
![]() .
.
Pour l'équation aux dérivées partielles suivante:
le système caractéristique associée s'écrit:
Deux intégrales premières solutions de (4.60) sont
![]() et
et
![]() . La solution générale de (4.59) est donc
. La solution générale de (4.59) est donc
![]() (surfaces de révolution).
(surfaces de révolution).
Soit l'équation de transport d'un scalaire
![]() par un champ de vitesse
par un champ de vitesse
![]()
le système caractéristique associée s'écrit:
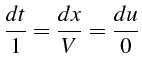
Les intégrales premières sont
![]() et la trajectoire
et la trajectoire
![]() du
champ de vitesse solution de
du
champ de vitesse solution de
![]() . La solution générale de (4.61)
est donc
. La solution générale de (4.61)
est donc
![]() le long des trajectoires du champ de vitesse.
le long des trajectoires du champ de vitesse.
Dans le cas d'un champ de vitesse constante
![]() , les trajectoires
sont les droites
, les trajectoires
sont les droites
![]() et la solution générale s'écrit
et la solution générale s'écrit
où
![]() est la solution initiale à
est la solution initiale à
![]() .
.
Dans le cas d'un champ de vitesse uniformément accéléré
![]() ,
les trajectoires sont des paraboles
,
les trajectoires sont des paraboles
![]() ,
et la solution générale s'écrit:
,
et la solution générale s'écrit: