suivant: 5. Annexe: EDP et monter: 4. Schémas différences finies précédent: 4.3 Équation des ondes Table des matières
On considère le problème de la dispersion d'un polluant à la surface
d'un liquide en mouvement (figure 4.15). Le polluant est
miscible dans le liquide, mais plus léger. On suppose que la vitesse
du fluide est horizontale. On peut alors considérer que le polluant
diffuse essentiellement à la surface, et négliger les variations suivant
la vertical
![]() .
.
En notant
![]() la fraction massique de polluant et
la fraction massique de polluant et
![]() la densité
du fluide, l'équation d'équilibre pour
la densité
du fluide, l'équation d'équilibre pour
![]() traduit que la variation
temporelle de la quantité de polluant
traduit que la variation
temporelle de la quantité de polluant
![]() dans un volume
élémentaire
dans un volume
élémentaire
![]() est égale à un bilan de flux de
est égale à un bilan de flux de
![]() sur les
facettes du volume. A travers une facette de surface
sur les
facettes du volume. A travers une facette de surface
![]() et de normale
sortante
et de normale
sortante
![]() , il existe un flux de diffusion
, il existe un flux de diffusion
![]() (
(
![]() est le coefficient de diffusion ) et un flux de convection
est le coefficient de diffusion ) et un flux de convection
![]() (
(
![]() est
la vitesse du fluide). L'équation d'équilibre s'écrit:
est
la vitesse du fluide). L'équation d'équilibre s'écrit:
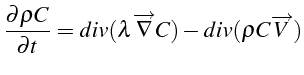
Compte tenu de l'équation de conservation de la masse du fluide:
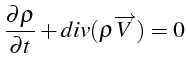
cette équation s'écrit:
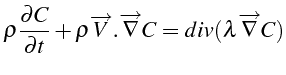
Compte tenu de l'hypothèse d'indépendance des quantités par rapport
à
![]() , et en supposant en outre que la densité
, et en supposant en outre que la densité
![]() et le coefficient
de diffusion
et le coefficient
de diffusion
![]() sont constants, il vient:
sont constants, il vient:
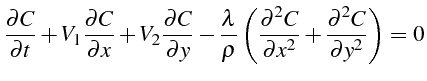
A cette équation il faut ajouter la condition initiale
![]() et des conditions aux limites sur les frontières
et des conditions aux limites sur les frontières
![]() du domaine
du domaine
![]() . On suppose que le polluant se trouve initialement à l'intérieur
du domaine
. On suppose que le polluant se trouve initialement à l'intérieur
du domaine
![]() et a pour dimension caractéristique
et a pour dimension caractéristique
![]() (figure 4.15). On distingue les frontières entrantes
(figure 4.15). On distingue les frontières entrantes
![]() ,
i.e. telle que
,
i.e. telle que
![]() et les frontières
sortantes
et les frontières
sortantes
![]() , i.e. telle que
, i.e. telle que
![]() .
Si la convection est prépondérante sur la diffusion, le flux entrant
sur les frontières
.
Si la convection est prépondérante sur la diffusion, le flux entrant
sur les frontières
![]() est un flux de convection qui apporte
du fluide non pollué dans le domaine
est un flux de convection qui apporte
du fluide non pollué dans le domaine
![]() . La condition sur
. La condition sur
![]() est une condition de Dirichlet
est une condition de Dirichlet
![]() . Sur les frontières
. Sur les frontières
![]() , le fluide transporte le polluant vers l'extérieur:
on impose alors une condition aux limites de Neumann
, le fluide transporte le polluant vers l'extérieur:
on impose alors une condition aux limites de Neumann
![]() ,
qui autorise la sortie du polluant du domaine
,
qui autorise la sortie du polluant du domaine
![]() .
.
Pour un domaine carré de dimension
![]() , et une vitesse
, et une vitesse
![]() avec des composantes positives
avec des composantes positives
![]() et
et
![]() , la frontière
, la frontière
![]() correspond aux deux cotés
correspond aux deux cotés
![]() et
et
![]() et la frontière
et la frontière
![]() aux deux autres cotés opposés
aux deux autres cotés opposés
![]() et
et
![]() .
.
En notant
![]() , le problème modèle s'écrit
pour un domaine
, le problème modèle s'écrit
pour un domaine
![]() carré de dimension caractéristique
carré de dimension caractéristique
![]() :
:
Trouver
![]() tel que:
tel que:
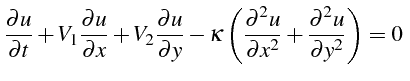 sur sur |
(4.26) |
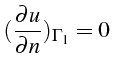 sur sur |
|
Le problème (4.26) est un problème d'évolution parabolique caractéristique des problèmes de mécanique des fluides, avec un terme de convection et un terme de diffusion. Nous allons tout d'abord effectuer une analyse d'ordre de grandeur de chacun de ces termes.
Soit
![]() la dimension caractéristique de la tache initiale,
l'ordre de grandeur des différents termes de l'équation (4.26)
s'écrit, en notant
la dimension caractéristique de la tache initiale,
l'ordre de grandeur des différents termes de l'équation (4.26)
s'écrit, en notant
![]() un temps caractéristique:
un temps caractéristique:
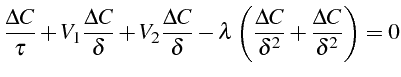
Si on considère uniquement la diffusion, le temps caractéristique vaut:
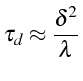
On retrouve le temps caractéristique de diffusion (relation c1tdiff)
calculé pour l'équation de la chaleur. Le temps caractéristique
![]() vérifie une relation du type (à rapprocher de la condition de stabilité
c1eq36 pour une équation de diffusion):
vérifie une relation du type (à rapprocher de la condition de stabilité
c1eq36 pour une équation de diffusion):
C'est le temps caractéristique de décroissance exponentielle des phénomènes de diffusion.
Si on considère uniquement la convection, le temps caractéristique vaut:
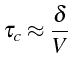
Ce temps correspond au temps de transport de la tache par le champ
de vitesse sur une distance égale à la dimension de la tache. Ce temps
caractéristique
![]() vérifie donc une relation du type (à rapprocher
de la condition de stabilité de Courant c3eq12):
vérifie donc une relation du type (à rapprocher
de la condition de stabilité de Courant c3eq12):
Pour notre problème, on peut définir un autre temps caractéristique
de convection: le temps de sortie
![]() du polluant hors du
domaine
du polluant hors du
domaine
![]() . Il est basé sur la dimension caractéristique
. Il est basé sur la dimension caractéristique
![]() du domaine et vérifie:
du domaine et vérifie:
Enfin le rapport entre les temps caractéristiques de diffusion
![]() et de convection
et de convection
![]() est le nombre de Péclet:
est le nombre de Péclet:
qui caractérise l'importance relative du terme de convection par rapport au terme de diffusion.
Considérons la condition initiale suivante:
qui décrit une tache gaussienne d'amplitude 1 centrée en
![]() ,
de rayon
,
de rayon
![]() .
.
S'il n'y a pas de convection, cette tache diffuse de façon auto-similaire , i.e. son amplitude diminue et son rayon augmente en conservant une forme gaussienne:
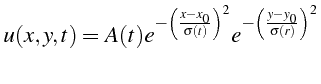
En utilisant la conservation globale de
![]() dans tout le domaine:
dans tout le domaine:
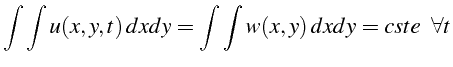
on en déduit la relation entre l'amplitude
![]() et le rayon
et le rayon
![]() :
:
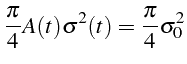
(l'intégrale d'une gaussienne vaut:
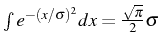 ).
).
On cherche donc une solution de diffusion de l'équation (4.26)
(avec
![]() ) sous la forme:
) sous la forme:
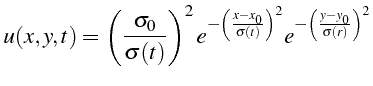
En reportant cette relation dans l'équation (4.26) on obtiens
l'équation d'évolution de
![]() :
:
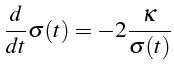
dont la solution vérifiant
![]() est:
est:
La solution de diffusion de l'équation (4.26) s'écrit donc:
L'amplitude de cette gaussienne décroît donc suivant la loi:
En prenant en compte la convection par un champ de vitesse sans cisaillement, cette tache gaussienne est transportée sans déformation et diffuse le long des trajectoires du champ de vitesse comme précédemment. Pour un champ de vitesse constant, les trajectoires sont des droites:
la solution de convection-diffusion de l'équation (4.26) s'écrit donc:
Cette solution est une solution en milieu infini et ne tiens pas compte
des conditions aux limites du problème (4.26). Elle constitue
cependant une bonne approximation de la solution, si la dimension
de la tache
![]() est petite devant la dimension
est petite devant la dimension
![]() du domaine
du domaine
![]() .
.
[solution a t=0 et t=0.5]![\includegraphics[width=0.25\paperwidth,keepaspectratio]{CHAP4/solexcdif}](img2061.png) [amplitude [amplitude ![\includegraphics[width=0.25\paperwidth,keepaspectratio]{CHAP4/solexcdif1}](img2062.png)
|
On a tracé l'évolution de cette solution (4.35) sur la figure
(4.16) pour
![]() ,
,
![]() et
et
![]() .
Pour ces valeurs des paramètres, un domaine de longueur
.
Pour ces valeurs des paramètres, un domaine de longueur
![]() , une
position initiale
, une
position initiale
![]() et
et
![]() , le
temps caractéristique de diffusion vaut
, le
temps caractéristique de diffusion vaut
![]() , celui
de convection
, celui
de convection
![]() , et le nombre de Péclet
, et le nombre de Péclet
![]() .
Le problème est donc à convection dominante. Au bout d'un temps
.
Le problème est donc à convection dominante. Au bout d'un temps
![]()
![]() , la tache est à la frontière du domaine avec
une amplitude qui a diminuée d'un tiers:
, la tache est à la frontière du domaine avec
une amplitude qui a diminuée d'un tiers:
![]() .
.
Pour rechercher des solutions vérifiant les conditions aux limites, on détermine tout d'abord les modes propres de diffusion en utilisant la méthode de séparation de variable décrite au paragraphe c1analytique. Le calcul est identique, et on montre facilement que les modes propres sont les fonctions suivantes:
qui vérifient les conditions aux limites:
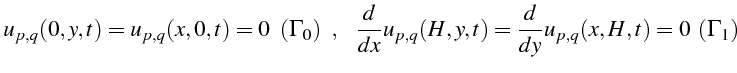
La solution générale de diffusion est alors une combinaison linéaire de ses modes:
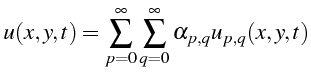
On a tracé sur la figure (4.17) le mode
![]() et
et
![]() ,
ainsi que l'évolution temporelle de son amplitude pour les mêmes paramètres
que précédemment (
,
ainsi que l'évolution temporelle de son amplitude pour les mêmes paramètres
que précédemment (
![]() ,
,
![]() ). Sur un temps
). Sur un temps
![]() ,
l'amplitude de ce mode décroît de
,
l'amplitude de ce mode décroît de
![]() .
.
Si on prend en compte la convection dans le cas d'un champ de vitesse sans cisaillement, la solution initiale est convectée sans déformation et diffusée le long des trajectoires. Par contre, il n'existe pas de solutions analytiques simples qui vérifient les conditions aux limites de (4.26).
En considérant une taille de structure
![]() ,
le temps caractéristique de diffusion vaut
,
le temps caractéristique de diffusion vaut
![]() ,
le temps caractéristique de convection
,
le temps caractéristique de convection
![]() , et le
nombre de Péclet
, et le
nombre de Péclet
![]() .
.
Nous avons vu dans les chapitres précédents qu'une discrétisation
précise de problème parabolique est le schéma de Cranck Nicholson.
Appliquée à l'équation (4.26), il s'écrit pour un maillage
cartésien de
![]() points suivant
points suivant
![]() et
et
![]() points suivant
points suivant
![]() , et de pas
, et de pas
![]() et
et
![]() :
:
C'est un schéma inconditionnellement stable d'ordre 2 en temps et
en espace, i.e. en
![]() .
.
A chaque itération en temps, on a à résoudre un système d'équations
linéaire
![]() , de
, de
![]() inconnues
inconnues
![]() . La matrice
. La matrice
![]() est une matrice penta-diagonale,
qui a la même structure que la matrice du laplacien au paragraphe
c4matlap. Pour des très gros maillages, le coût de résolution
de ce système linéaire en utilisant les méthodes de résolution du
paragraphe c4matlap peut devenir rapidement prohibitif.
est une matrice penta-diagonale,
qui a la même structure que la matrice du laplacien au paragraphe
c4matlap. Pour des très gros maillages, le coût de résolution
de ce système linéaire en utilisant les méthodes de résolution du
paragraphe c4matlap peut devenir rapidement prohibitif.
On va donc étudier dans le paragraphe suivant une méthode alternative: la méthode des directions alternées implicites.
Le principe des méthodes des directions alternées implicites, notées
ADI (ADI=Alternated Directions Implicited est le sigle classique des
directions alternées en anglais), est de décomposer les opérateurs
spatiaux suivant les directions d'espace
![]() et
et
![]() . On écrit l'équation
(4.26) sous la forme symbolique suivante:
. On écrit l'équation
(4.26) sous la forme symbolique suivante:
où
![]() et
et
![]() sont les deux opérateurs suivants:
sont les deux opérateurs suivants:
En notant
![]() ,
,
![]() ,
,
![]() les solutions
au temps
les solutions
au temps
![]() ,
,
![]() et
et
![]() ,
les développements limitées de
,
les développements limitées de
![]() peuvent s'écrire
de façon symbolique:
peuvent s'écrire
de façon symbolique:
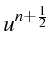 |
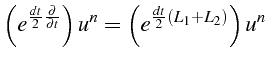 |
||
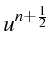 |
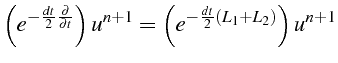 |
On a utilisé dans ces relations le fait que
![]() et
et
![]() sont solutions de l'équation exacte (4.26) pour remplacer
sont solutions de l'équation exacte (4.26) pour remplacer
![]() en fonction de
en fonction de
![]() et
et
![]() .
.
En combinant ces deux équations, il vient:
En utilisant un développement au premier ordre des exponentielles,
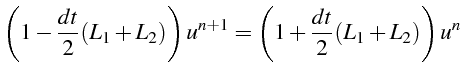
on obtiens le schéma suivant, dans lequel il suffit d'inclure l'approximation
spatiale des opérateurs
![]() et
et
![]() :
:
C'est le schéam classique de Cranck Nicholson (4.37).
Pour les schémas ADI, on effectue tout d'abord une factorisation formelle dans (4.40):
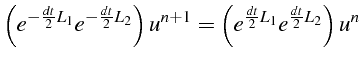
avant le développement limité des exponentielles:
Formellement, on a un schéma de type Cranck Nicholson d'ordre 2 mais
avec une erreur de troncature différente. Pour résoudre, on introduit
la solution intermédiaire
![]() telle que:
telle que:
Ces deux équations sont équivalentes à l'équation (4.42).
Pour s'en convaincre, il suffit de multiplier la première par
![]() et la seconde par
et la seconde par
![]() et de les combiner. L'intérêt
de cette procédure par rapport à Cranck Nicholson classique est que
dans la première équation (4.43), on est implicite suivant
et de les combiner. L'intérêt
de cette procédure par rapport à Cranck Nicholson classique est que
dans la première équation (4.43), on est implicite suivant
![]() (i.e. suivant
(i.e. suivant
![]() ) et explicite suivant
) et explicite suivant
![]() (i.e. suivant
(i.e. suivant
![]() ), et vice-versa dans la seconde. La résolution de ces deux équations
sera donc plus facile que la résolution du schéma de Cranck Nicholson
(4.41), dans lequel on est implicite suivant les 2 directions
), et vice-versa dans la seconde. La résolution de ces deux équations
sera donc plus facile que la résolution du schéma de Cranck Nicholson
(4.41), dans lequel on est implicite suivant les 2 directions
![]() et
et
![]() .
.
On discrétise ensuite les opérateurs
![]() et
et
![]() avec des
différences finies centrées sur un maillage cartésien de
avec des
différences finies centrées sur un maillage cartésien de
![]() points suivant
points suivant
![]() et
et
![]() points suivant
points suivant
![]() , et de pas
, et de pas
![]() et
et
![]() :
:
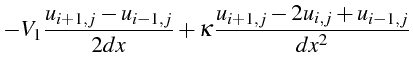 |
|||
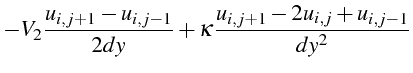 |
Ces équations ADI correspondent à deux discrétisations de l'équation
(4.26) à
![]() avec un pas en temps
avec un pas en temps
![]() .
La première correspond à une discrétisation entre
.
La première correspond à une discrétisation entre
![]() et
et
![]() avec une implicitation dans la direction
avec une implicitation dans la direction
![]() et la seconde à une
discrétisation entre
et la seconde à une
discrétisation entre
![]() et
et
![]() avec une implicitation
dans la direction
avec une implicitation
dans la direction
![]() (figure 4.18). La variable intermédiaire
(figure 4.18). La variable intermédiaire
![]() corresponds donc à une approximation de
corresponds donc à une approximation de
![]() .
.
La première équation (4.44) couple les valeurs inconnues
![]() par ligne (figure 4.18), i.e. les valeurs
inconnues sur la ligne
par ligne (figure 4.18), i.e. les valeurs
inconnues sur la ligne
![]()
![]() sont indépendantes
des valeurs sur les autres lignes. Elles sont solutions du système
linéaire tri-diagonal
sont indépendantes
des valeurs sur les autres lignes. Elles sont solutions du système
linéaire tri-diagonal
![]() de dimension
de dimension
![]() suivant:
suivant:
avec
![]() ,
,
![]() ,
,
![]() , et
, et
![]() ,
,
![]() ,
,
![]() .
.
Le second membre
![]() peut s'écrire sous la forme d'un
produit matrice vecteur
peut s'écrire sous la forme d'un
produit matrice vecteur
![]() avec une matrice
avec une matrice
![]() tridiagonale:
tridiagonale:
![\bgroup\color{black}$\displaystyle \mathcal{B}^{1}=\left[\begin{array}{ccccc}
\d...
..._{i,j-1}^{n}\\
u_{i,j}^{n}\\
u_{i,j+1}^{n}\\
\vdots\end{array}\right]$\egroup](img2147.png)
Pour déterminer les valeurs inconnues
![]() , il faut donc
résoudre
, il faut donc
résoudre
![]() systèmes linéaires tri-diagonaux de dimension
systèmes linéaires tri-diagonaux de dimension
![]() .
.
De même la seconde équation (4.45) couple les valeurs inconnues
![]() par colonne (figure 4.18), i.e. les valeurs
inconnues sur la colonne
par colonne (figure 4.18), i.e. les valeurs
inconnues sur la colonne
![]()
![]() sont
indépendantes des valeurs sur les autres colonnes. Elles sont solutions
du système linéaire tri-diagonal
sont
indépendantes des valeurs sur les autres colonnes. Elles sont solutions
du système linéaire tri-diagonal
![]() de dimension
de dimension
![]() suivant:
suivant:
avec
![]() ,
,
![]() ,
,
![]() , et
, et
![]() ,
,
![]() ,
,
![]() .
.
Le second membre
![]() peut encore s'écrire sous la forme
d'un produit matrice vecteur
peut encore s'écrire sous la forme
d'un produit matrice vecteur
![]() :
:
![\bgroup\color{black}$\displaystyle \mathcal{B}^{2}=\left[\begin{array}{ccccc}
\d...
..._{i-1,j}^{*}\\
u_{i,j}^{*}\\
u_{i+1,j}^{*}\\
\vdots\end{array}\right]$\egroup](img2160.png)
Pour déterminer valeurs inconnues
![]() , il faut donc résoudre
, il faut donc résoudre
![]() systèmes linéaires tri-diagonaux de dimension
systèmes linéaires tri-diagonaux de dimension
![]() .
.
A chaque itération en temps, on résoud
![]() systèmes tri-diagonaux
de rang
systèmes tri-diagonaux
de rang
![]() et
et
![]() systèmes tri-diagonaux de rang
systèmes tri-diagonaux de rang
![]() ,
ce qui est beaucoup plus efficace que la résolution d'un seul système
linéaire de rang
,
ce qui est beaucoup plus efficace que la résolution d'un seul système
linéaire de rang
![]() .
.
Pour les conditions aux limites, il faut modifier la première et la
dernière ligne de ces systèmes linéaires. Pour les conditions de Dirichlet
sur
![]() , on modifie la première ligne de
, on modifie la première ligne de
![]() et
et
![]() :
:
Cette condition fixe la valeur de la première ligne de
![]() :
:
![]() et la première colonne de
et la première colonne de
![]() :
:
![]() .
.
Pour les conditions de Neumann sur
![]() , on utilise une condition
miroir, qui modifie la dernière ligne de
, on utilise une condition
miroir, qui modifie la dernière ligne de
![]() et
et
![]() :
:
De même le second membre
![]() de l'étape 1 pour la ligne
de l'étape 1 pour la ligne
![]() est modifié:
est modifié:
ainsi que le second membre
![]() de l'étape 2 pour la
colonne
de l'étape 2 pour la
colonne
![]() :
:
L'étude de la stabilité utilise le programme Maple 4.4.4.
> restart:
# Equation de convection-diffusion
> diff(U(x,y,t),t)+V1*diff(U(x,y,t),x)+V2*diff(U(x,y,t),y)=
> kappa*(diff(U(x,y,t),x$2)+diff(U(x,y,t),y$2));eq:=%:
# Schema ADI
> (U[ns,i,j]-U[n,i,j])/(dt/2)+V1*(U[ns,i+1,j]-U[ns,i-1,j])/
(2*dx)+V2*(U[n,i,j+1]-U[n,i,j-1])/(2*dy)=kappa*((U[ns,i+1,j]
-2*U[ns,i,j]+U[ns,i-1,j])/dx^2+(U[n,i,j+1]-2*U[n,i,j]+
U[n,i,j-1])/dy^2); eqh1:=%:
> (U[n+1,i,j]-U[ns,i,j])/(dt/2)+V1*(U[ns,i+1,j]-U[ns,i-1,j])/
(2*dx)+V2*(U[n+1,i,j+1]-U[n+1,i,j-1])/(2*dy)=kappa*((U[ns,i+1,j]
-2*U[ns,i,j]+U[ns,i-1,j])/dx^2+(U[n+1,i,j+1]-2*U[n+1,i,j]+
U[n+1,i,j-1])/dy^2); eqh2:=%:
# Etude de la Stabilite
> Up:=(n,i,j)->Psi[n]*exp(I*omega[1]*i*dx)*exp(I*omega[2]*j*dy);
> subs(U[ns,i,j]=Up(ns,i,j),U[n,i,j]=Up(n,i,j),
U[ns,i+1,j]=Up(ns,i+1,j),U[ns,i-1,j]=Up(ns,i-1,j),
U[n,i,j+1]=Up(n,i,j+1),U[n,i,j-1]=Up(n,i,j-1),eqh1):
> rel1:=simplify(%*exp(-I*omega[1]*i*dx)*exp(-I*omega[2]*j*dy)):
> Psi[ns]/Psi[n]=solve(subs(Psi[ns]=G*Psi[n],rel1),G);rel11:=%:
#
> subs(U[ns,i,j]=Up(ns,i,j),U[n+1,i,j]=Up(n+1,i,j),
U[ns,i+1,j]=Up(ns,i+1,j),U[ns,i-1,j]=Up(ns,i-1,j),
U[n+1,i,j+1]=Up(n+1,i,j+1),U[n+1,i,j-1]=Up(n+1,i,j-1),eqh2):
> rel2:=simplify(%*exp(-I*omega[1]*i*dx)*exp(-I*omega[2]*j*dy)):
> Psi[n+1]/Psi[ns]=solve(subs(Psi[n+1]=G*Psi[ns],rel2),G);
rel22:=%:
# Facteur d'amplification
> G:=rhs(rel11)*rhs(rel22);
# Etude de chaque terme
> A1=r1*(1-cos(omega[1]*dx));A2=r2*(1-cos(omega[2]*dy));
> rel1:={%,%%}: rel11:={r1=kappa*dt/dx^2,r2=kappa*dt/dy^2}:
> B1=CFL1*sin(omega[1]*dx)/2;B2=CFL2*sin(omega[2]*dy)/2;
> rel2:={%,%%}: rel22:={CFL1=V1*dt/dx,CFL2=V2*dt/dy}:
> 'G'=((A1-1)+I*B1)/((A1+1)+I*B1)*((A2-1)+I*B2)/((A2+1)+I*B2);
GG:=rhs(%):
# Verification
> G=subs(rel1,rel2,rel11,rel22,GG):simplify(%):rhs(%)-lhs(%);
# Calcul du carre du module de G
> GG;
> G1:=((A1-1)+I*B1)/((A1+1)+I*B1);
G1M=((A1-1)^2+B1^2)/((A1+1)^2+B1^2);
> G2:=((A2-1)+I*B2)/((A2+1)+I*B2);
G2M=((A2-1)^2+B2^2)/((A2+1)^2+B2^2);
# G1M et G2M sont donc <1 ==> donc stabilite
On définit les deux étapes (4.44 et 4.45) du schéma
ADI (lignes 6 à 13), puis on introduit une perturbation
![]() décomposée
en mode de Fourier (ligne 15), que l'on introduit dans les deux équations
(lignes 16 et 22). On calcul l'amplification du mode pour chacune
de ces équations: i.e.
décomposée
en mode de Fourier (ligne 15), que l'on introduit dans les deux équations
(lignes 16 et 22). On calcul l'amplification du mode pour chacune
de ces équations: i.e.
![]() pour la première
(ligne 20) et
pour la première
(ligne 20) et
![]() pour la seconde (ligne
22). D'où l'on déduit le facteur d'amplification global du schéma
pour la seconde (ligne
22). D'où l'on déduit le facteur d'amplification global du schéma
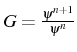 (ligne 29):
(ligne 29):
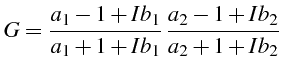
avec
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Le carré du module de
![]() vaut:
vaut:
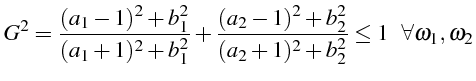
Il est plus petit que 1 puisque
Le schéma ADI (4.44 et 4.45) est donc inconditionnellement stable.
Pour étudier la consistance, on utilise le programme Maple 4.4.4, qui est la suite du programme précédent 4.4.4.
# Erreur de troncature dvt de taylor autour de t=n+1/2
# Equation equivalente
> 1/2*eqh1+1/2*eqh2:eqh12:=lhs(%)-rhs(%):
# subsitution de la solution exacte dans cette equation
> Uex:=(r,p,q)->U(x+(p-i)*dx,y+(q-j)*dy,t+(r-n-1/2)*dt);
> subs(U[n,i,j]=Uex(n,i,j),
U[n,i+1,j]=Uex(n,i+1,j),U[n,i-1,j]=Uex(n,i-1,j),
U[n,i,j+1]=Uex(n,i,j+1),U[n,i,j-1]=Uex(n,i,j-1),
U[n+1,i,j]=Uex(n+1,i,j),
U[n+1,i+1,j]=Uex(n+1,i+1,j),U[n+1,i-1,j]=Uex(n+1,i-1,j),
U[n+1,i,j+1]=Uex(n+1,i,j+1),U[n+1,i,j-1]=Uex(n+1,i,j-1),
U[ns,i,j]=Uex(n+1/2,i,j),
U[ns,i+1,j]=Uex(n+1/2,i+1,j),U[ns,i-1,j]=Uex(n+1/2,i-1,j),
U[ns,i,j+1]=Uex(n+1/2,i,j+1),U[ns,i,j-1]=Uex(n+1/2,i,j-1),
eqh12); eqh3:=%:
# Developpement de Taylor autour de t=n+1/2
> k:=6:
> U(x,y,t-dt/2)=convert(mtaylor(U(x,y,t-dt/2),[dt],k),diff):
S1:=%:
> U(x,y+dy,t-dt/2)=convert(mtaylor(U(x,y+dy,t-dt/2),[dy,dt],
k),diff): S2:=%:
> U(x,y-dy,t-dt/2)=convert(mtaylor(U(x,y-dy,t-dt/2),[dy,dt],
k),diff):S3:=%:
> U(x+dx,y,t-dt/2)=convert(mtaylor(U(x+dx,y,t-dt/2),[dx,dt],
k),diff):S4:=%:
> U(x-dx,y,t-dt/2)=convert(mtaylor(U(x-dx,y,t-dt/2),[dx,dt],
k),diff):S5:=%:
> U(x,y+dy,t)=convert(mtaylor(U(x,y+dy,t),[dy],k),diff):
S6:=%:
> U(x,y-dy,t)=convert(mtaylor(U(x,y-dy,t),[dy],k),diff):
S7:=%:
> U(x+dx,y,t)=convert(mtaylor(U(x+dx,y,t),[dx],k),diff):
S8:=%:
> U(x-dx,y,t)=convert(mtaylor(U(x-dx,y,t),[dx],k),diff):
S9:=%:
> U(x,y,t+dt/2)=convert(mtaylor(U(x,y,t+dt/2),[dt],k),diff):
S10:=%:
> U(x,y+dy,t+dt/2)=convert(mtaylor(U(x,y+dy,t+dt/2),[dy,dt],
k),diff):S11:=%:
> U(x,y-dy,t+dt/2)=convert(mtaylor(U(x,y-dy,t+dt/2),[dy,dt],
k),diff):S12:=%:
> U(x+dx,y,t+dt/2)=convert(mtaylor(U(x+dx,y,t+dt/2),[dx,dt],
k),diff):S13:=%:
> U(x-dx,y,t+dt/2)=convert(mtaylor(U(x-dx,y,t+dt/2),[dx,dt],
k),diff): S14:=%:
# substitution dans l'équation discrete - equation exacte
> subs(S1,S2,S3,S4,S5,S6,S7,S8,S9,S10,S11,S12,S13,S14,eqh3)-
(lhs(eq)-rhs(eq)):
> simplify(%):collect(%,{dt,dx,dy});
# Schema d'ordre 2 en dt,dx et dy
Pour cela on fait la demi somme des deux équations (4.44 et 4.45) pour obtenir une équation discrète équivalente à l'équation exacte (4.26) (ligne 3):
En comparant cette équation (4.52) au schéma de Cranck Nicholson
(4.37), on peut retrouver ce dernier en remplaçant simplement
dans (4.52) les valeurs de
![]() par la moyenne
par la moyenne
![]() . Ce schéma ADI est donc
bien équivalent au schèma de Cranck Nicolson. Les valeurs intermédiaires
. Ce schéma ADI est donc
bien équivalent au schèma de Cranck Nicolson. Les valeurs intermédiaires
![]() sont des approximations de la solution à
sont des approximations de la solution à
![]() .
.
Dans l'équation équivalente (4.52), on substitue la solution
approchée par la solution exacte (lignes 6 à 15), et on effectue des
développements limités autour de
![]() (lignes
18 à 45). Après soustraction de l'équation exacte, on obtient l'erreur
de troncature
(lignes
18 à 45). Après soustraction de l'équation exacte, on obtient l'erreur
de troncature
![]() , qui est en
, qui est en
![]() .
.
Le schéma ADI (4.44 et 4.45) est donc
consistant avec l'équation exacte (4.26), et est d'ordre
2 en temps et en espace, i.e. en
![]() .
.
Le programme Matlab (4.4.5) implémente le schéma ADI en utilisant une programmation matricielle.
% resolution ADI
clear
% maillage
L=1; H=1;
Nx=51; dx=L/(Nx-1); X=[0:dx:L];
Ny=51; dy=H/(Ny-1); Y=[0:dy:H];
% champ vitesse
v1=1; v2=1;
% parametres
kappa=0.01; dt=0.001; Tf=0.5; nit=round(Tf/dt)
% champ initial
delta=(0.1)^2; x0=L/4; y0=H/4;
Ui=exp(-(X-x0).^2/delta)'*exp(-(Y-y0).^2/delta);
Un=Ui; Us=Ui; Un1=Ui;
% matrices 3D
I1=ones(1,Nx); I2=ones(1,Ny);
A1 =[-kappa/dx^2-v1/(2*dx); 2/dt+2*kappa/dx^2; ...
-kappa/dx^2+v1/(2*dx)]*I1;
C1=[ kappa/dy^2+v2/(2*dy); 2/dt-2*kappa/dy^2; ...
kappa/dy^2-v2/(2*dy)]*I1;
A2 =[-kappa/dy^2-v2/(2*dy); 2/dt+2*kappa/dy^2; ...
-kappa/dy^2+v2/(2*dy)]*I2;
C2=[ kappa/dx^2+v1/(2*dx); 2/dt-2*kappa/dx^2; ...
kappa/dx^2-v1/(2*dx)]*I2;
% C.L de Dirichlet en i=1 j=1
A1(:,1)=0; A1(2,1)=1; C1(:,1)=0;
A2(:,1)=0; A2(2,1)=1; C2(:,1)=0;
% C.L de Neumann sur les frontieres i=Nx j=Ny
A1(1,Nx)=A1(1,Nx)+A1(3,Nx); A1(3,Nx)=0;
A2(1,Ny)=A2(1,Ny)+A2(3,Ny); A2(3,Ny)=0;
% iterations en temps
for it=1:nit
% 1ere etape ADI
Us(1:Nx,1)=0;
for j=2:Ny-1
B1=C1(1,1:Nx)'.*Un(1:Nx,j-1)+C1(2,1:Nx)'.*Un(1:Nx,j)+...
C1(3,1:Nx)'.*Un(1:Nx,j+1);
Us(1:Nx,j)=tridiag(A1,B1);
end;
B1=C1(2,1:Nx)'.*Un(1:Nx,Ny)+(C1(1,1:Nx)+...
C1(3,1:Nx))'.*Un(1:Nx,Ny-1);
Us(1:Nx,Ny)=tridiag(A1,B1);
% 2nd etape ADI
Un1(1,1:Ny)=0;
for i=2:Nx-1
B2=C2(1,1:Ny)'.*Us(i-1,1:Ny)'+C2(2,1:Ny)'.*Us(i,1:Ny)'+...
C2(3,1:Ny)'.*Us(i+1,1:Ny)';
Un1(i,1:Ny)=tridiag(A2,B2)';
end;
B2=C2(2,1:Ny)'.*Us(Nx,1:Ny)'+...
(C2(1,1:Ny)+C2(3,1:Ny))'.*Us(Nx-1,1:Ny)';
Un1(Nx,1:Ny)=tridiag(A2,B2)';
% iteration suivante
Un=Un1;
end;
Les paramètres du calcul sont définis aux lignes 4 à 10. Les matrices tridiagonales sont construites sur les lignes 17 à 24, puis on applique les conditions aux limites (lignes 26 à 30).
La boucle en temps (lignes 32 à 55) inclus les deux étapes ADI et utilise la fonction tridiag (lin3D) pour la résolution des systèmes linéaires tri-diagonaux.
Pour valider ce programme, nous avons tout d'abord simuler la diffusion
du mode propre (4.36)
![]() et
et
![]() avec un maillage
de
avec un maillage
de
![]() points dans chaque direction et un paramètre
points dans chaque direction et un paramètre
![]() . La solution calculée au bout d'un temps
. La solution calculée au bout d'un temps
![]() avec
avec
![]() est tracée sur la figure (4.19). L'allure
de la solution (figure 4.19a) coïncide bien avec la solution
exacte (figure 4.17a) , ce que confirme le tracé de l'évolution
temporelle de la solution au point
est tracée sur la figure (4.19). L'allure
de la solution (figure 4.19a) coïncide bien avec la solution
exacte (figure 4.17a) , ce que confirme le tracé de l'évolution
temporelle de la solution au point
![]() ,
,
![]() comparée à la solution
exacte (figure 4.19b).
comparée à la solution
exacte (figure 4.19b).
Pour tester la précision d'intégration en temps du schéma, nous avons
calculer l'erreur au point (
![]() ,
,
![]() ) au bout du temps
) au bout du temps
![]() (de l'ordre du temps caractéristique de diffusion), en fonction du
pas d'intégration en temps
(de l'ordre du temps caractéristique de diffusion), en fonction du
pas d'intégration en temps
![]() . Le résultat de la figure (4.20a)
montre que pour les pas en temps choisis l'erreur est quasiment indépendante
du pas en temps
. Le résultat de la figure (4.20a)
montre que pour les pas en temps choisis l'erreur est quasiment indépendante
du pas en temps
![]() , et est donc essentiellement une erreur de discrétisation
spatiale. On note que les pas en temps choisis sont tels que le pas
en temps est beaucoup plus faible que le temps caractéristique de
diffusion:
, et est donc essentiellement une erreur de discrétisation
spatiale. On note que les pas en temps choisis sont tels que le pas
en temps est beaucoup plus faible que le temps caractéristique de
diffusion:
![]()
[Erreur temporelle ![\includegraphics[width=0.25\paperwidth,keepaspectratio]{CHAP4/errhdif}](img2197.png) [erreur spatiale [erreur spatiale ![\includegraphics[width=0.25\paperwidth,keepaspectratio]{CHAP4/errhdif1}](img2198.png)
|
Nous l'avons vérifié en faisant varier le nombre de points du maillage
de
![]() à
à
![]() avec un pas en temps
avec un pas en temps
![]() fixé. L'évolution de l'erreur en fonction du pas de discrétisation
spatiale
fixé. L'évolution de l'erreur en fonction du pas de discrétisation
spatiale
![]() est tracée sur la figure (4.20b), et
on constate que l'erreur décroît en
est tracée sur la figure (4.20b), et
on constate que l'erreur décroît en
![]() .
.
Pour cette condition initiale, nous avons aussi fait une simulation
avec une vitesse de convection non nulle
![]() . Ce cas
correspond à un nombre de Péclet
. Ce cas
correspond à un nombre de Péclet
![]() . Les iso-valeurs de
la solution sont tracées sur la figure (4.21).
. Les iso-valeurs de
la solution sont tracées sur la figure (4.21).
On note la convection sans déformation de la solution initiale, ce
qui confirme que la condition aux limites sur
![]() autorise
la sortie des structures hors du domaine. On a aussi comparé l'évolution
temporelle du maximum de la solution exacte de diffusion et du maximum
de la solution calculée, que l'on a tracé sur la figure (4.22a).
On vérifie ainsi que la décroissance de la solution est une décroissance
visqueuse.
autorise
la sortie des structures hors du domaine. On a aussi comparé l'évolution
temporelle du maximum de la solution exacte de diffusion et du maximum
de la solution calculée, que l'on a tracé sur la figure (4.22a).
On vérifie ainsi que la décroissance de la solution est une décroissance
visqueuse.
Nous avons ensuite étudié l'influence du pas d'intégration en temps
![]() , en traçant sur la figure (4.22b) l'écart en fonction
de
, en traçant sur la figure (4.22b) l'écart en fonction
de
![]() entre le maximum de la solution exacte de diffusion et le
maximum de la solution calculée. On constate que cet écart croît rapidement
en dessus d'une valeur
entre le maximum de la solution exacte de diffusion et le
maximum de la solution calculée. On constate que cet écart croît rapidement
en dessus d'une valeur
![]() . Cette valeur est justement de l'ordre
de grandeur du temps caractéristique de convection
. Cette valeur est justement de l'ordre
de grandeur du temps caractéristique de convection
![]() .
.
En conclusion sur cette simulation, on note que le choix des paramètres numériques a été fixé par la physique du problème, et non par des conditions numériques de stabilité:
Le second cas de calcul correspond à la condition initiale gaussienne (4.31), avec les mêmes paramètres qu'au paragraphe c4gpar.
Pour un maillage
![]() et un pas en temps
et un pas en temps
![]() ,
on a tracé sur la figure (4.23a) la solution à
,
on a tracé sur la figure (4.23a) la solution à
![]() et
à
et
à
![]() . Cette solution se compare très bien avec la solution exacte
tracée sur la figure (4.16). On a aussi comparé l'évolution
temporelle de l'amplitude de la tache gaussienne calculée avec le
schéma ADI avec l'expression analytique (4.34). Ces deux
courbes coïncident, ainsi que le montre la figure (4.23b).
. Cette solution se compare très bien avec la solution exacte
tracée sur la figure (4.16). On a aussi comparé l'évolution
temporelle de l'amplitude de la tache gaussienne calculée avec le
schéma ADI avec l'expression analytique (4.34). Ces deux
courbes coïncident, ainsi que le montre la figure (4.23b).
Nous avons effectué une seconde simulation avec un coefficient de
diffusion plus petit
![]() . Dans ce cas, la solution numérique
présente des oscillations (figure 4.24). Pour cette valeur
de
. Dans ce cas, la solution numérique
présente des oscillations (figure 4.24). Pour cette valeur
de
![]() , le nombre de Péclet de maille:
, le nombre de Péclet de maille:
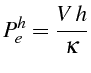
vaut
![]() au lieu de
au lieu de
![]() avec la valeur de
avec la valeur de
![]() précédente. Sur le tracé des iso-valeurs (4.24a), on constate
l'apparition de légères oscillations, caractérisées par la présence
de nombreuses lignes iso-valeurs
précédente. Sur le tracé des iso-valeurs (4.24a), on constate
l'apparition de légères oscillations, caractérisées par la présence
de nombreuses lignes iso-valeurs
![]() , qui n'existent pas à
, qui n'existent pas à
![]() (figure 4.24b). Le tracé d'un profil à
(figure 4.24b). Le tracé d'un profil à
![]() (figure
4.24c) montre bien l'apparition d'une oscillation numérique
au pied de la tache gaussienne. Ces oscillations numériques sont de
même nature que celles étudiées au paragraphe c3centre du
chapitre précédent. Elles apparaissent dès que le Péclet de maille
(figure
4.24c) montre bien l'apparition d'une oscillation numérique
au pied de la tache gaussienne. Ces oscillations numériques sont de
même nature que celles étudiées au paragraphe c3centre du
chapitre précédent. Elles apparaissent dès que le Péclet de maille
![]() devient plus grand que 2 et indiquent que le maillage
n'est plus suffisamment fin pour capter la solution de convection
avec ce schéma centré.
devient plus grand que 2 et indiquent que le maillage
n'est plus suffisamment fin pour capter la solution de convection
avec ce schéma centré.