suivant: 4.4 Équation de convection-diffusion monter: 4. Schémas différences finies précédent: 4.2 Équation de Poisson Table des matières
On s'intéresse aux oscillations de la surface d'un liquide contenu
dans un réservoir. Au repos le réservoir contient un liquide sur une
hauteur
![]() . La surface du liquide est plane, horizontale et
notée
. La surface du liquide est plane, horizontale et
notée
![]() . La répartition de pression dans le liquide est hydrostatique:
. La répartition de pression dans le liquide est hydrostatique:
On perturbe la surface
![]() à l'instant initiale. Celle ci
se met alors à osciller de part et d'autre de sa position initiale
à l'instant initiale. Celle ci
se met alors à osciller de part et d'autre de sa position initiale
![]() . On néglige les effets de viscosité, et on applique les équations
de conservation de la masse et de la quantité de mouvement à un cylindre
élémentaire de base
. On néglige les effets de viscosité, et on applique les équations
de conservation de la masse et de la quantité de mouvement à un cylindre
élémentaire de base
![]() et de hauteur
et de hauteur
![]() (figure 4.7).
(figure 4.7).
En notant
![]() la
vitesse moyenne (suivant z) et
la
vitesse moyenne (suivant z) et
![]() la densité, le bilan de masse
pour le cylindre de volume
la densité, le bilan de masse
pour le cylindre de volume
![]() s'écrit:
s'écrit:
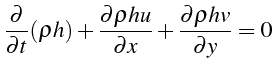
De même le bilan de quantité de mouvement s'écrit:
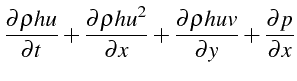 |
0 | ||
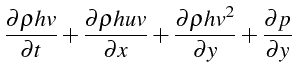 |
0 |
En notant que
![]() ,
,
![]() et en linéarisant
les équations précédentes (
et en linéarisant
les équations précédentes (
![]() ,
,
![]() ,
,
![]() ), il vient:
), il vient:
En dérivant la première équation par rapport à
![]() , la seconde par
rapport à
, la seconde par
rapport à
![]() et la troisième par rapport à
et la troisième par rapport à
![]() , on obtiens l'équation
de propagation de la perturbation
, on obtiens l'équation
de propagation de la perturbation
![]() de la surface libre en éliminant
de la surface libre en éliminant
![]() et
et
![]() :
:
C'est une équation des ondes qui traduit la propagation d'ondes de
surface avec une célérité
![]() .
.
A cette équation, il faut ajouter une condition aux limites sur la
frontière
![]() du réservoir. La condition physique est la condition
de vitesse normale nulle
du réservoir. La condition physique est la condition
de vitesse normale nulle
![]() sur
sur
![]() . Pour obtenir une condition sur
. Pour obtenir une condition sur
![]() , on utilise la
combinaison suivant
, on utilise la
combinaison suivant
![]() des 2 dernières équations
(4.7):
des 2 dernières équations
(4.7):
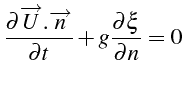
d'où l'on déduit la condition aux limites sur
![]() :
:
Les conditions initiales sont données par la déformation initiale
![]() et la vitesse de cette déformation. En supposant la vitesse
de déformation initiale nulle, on a donc:
et la vitesse de cette déformation. En supposant la vitesse
de déformation initiale nulle, on a donc:
Le problème modèle associé s'écrit:
Trouvez
![]() tel que
tel que
Dans le cas d'un domaine
![]() circulaire de rayon
circulaire de rayon
![]() , on
peut avantageusement passer en coordonnées polaires
, on
peut avantageusement passer en coordonnées polaires
![]() .
Le problème modèle s'écrit:
.
Le problème modèle s'écrit:
Trouver
![]() tel que:
tel que:
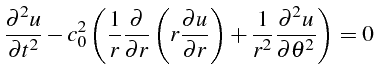 dans dans |
(4.12) |
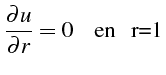 |
|
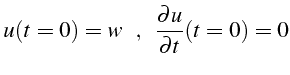 |
Dans la cas cylindrique (4.12), on a cherché la solution analytique à l'aide du programme Maple (4.3.2).
> restart;with(plots):
# Equation des ondes en polaire
> diff(u(r,theta,t),t$2)=c0^2/r*diff(r*diff(u(r,theta,t),r),r)
+c0^2/r^2*diff(u(r,theta,t),theta$2);
> eq:=%:
# Solutions en variables séparées de type onde periodique en theta
> u(r,theta,t)=A(r)*exp(I*k*theta)*exp(I*lambda*c0*t);
> subs(%,eq):simplify(%/exp(I*k*theta)/exp(I*lambda*c0*t)/c0^2);
eq1:=%:
> rhs(eq1)-lhs(eq1);eq2:=%:
> dsolve(eq2,A(r));
# Modes propres
> Ue:=(r,theta,t)->BesselJ(k,lambda*r)*exp(I*k*theta)*exp(I*lambda*c0*t);
> subs(r=1,diff(Ue(r,theta,t),r));
# Pour chaque valeur de k, on calcule les racines lambda
> -BesselJ(k+1,lambda)+k*BesselJ(k,lambda)/lambda=0; eq3:=lhs(%):
> plot({subs(k=0,eq3),subs(k=1,eq3),subs(k=2,eq3)},lambda=0..20);
> Um:=(k,p)->BesselJ(k,lambda[k,p]*r)*exp(I*k*theta)*exp(I*lambda[k,p]*c0*t);
> Uex=sum(sum(C[k,p]*Um(k,p),p=0..M),k=0..N);
# Conditions initiales particulieres (avec c0=1)
# 1/ mode radial
> lambda1:=fsolve(subs(k=0,eq3),lambda,10..12);
> Uex1:=BesselJ(0,lambda1*r)*cos(lambda1*t);
> animate3d([r*cos(theta),r*sin(theta),Uex1],r=0..1,theta=0..2*Pi,
t=0..2*(2*Pi/lambda1),frames=50);
# 2/ mode angulaire
> lambda2:=fsolve(subs(k=1,eq3),lambda,6..10);
> Uex2:=BesselJ(1,lambda2*r)*cos(lambda2*t)*cos(theta);;
> animate3d([r*cos(theta),r*sin(theta),Uex2],r=0..1,theta=0..2*Pi,
t=0..2*(2*Pi/lambda2),frames=50);
On a cherché une solution élémentaire à variables séparées sous la
forme d'une onde se propageant à une célérité
![]() et
périodique en
et
périodique en
![]() (ligne 7):
(ligne 7):

En reportant dans l'équation, on obtiens une équation de Bessel (ligne
9) pour
![]() :
:
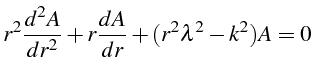
dont Maple nous fournit la solution générale avec la fonction dsolve
(ligne 11). Cette solution générale est une combinaison linéaire de
fonctions de Bessel de première et deuxième espèce:
![]() et
et
![]() . De ces deux familles de fonctions de Bessel, on ne retient
que la famille
. De ces deux familles de fonctions de Bessel, on ne retient
que la famille
![]() , qui est la seule a avoir une valeur finie
(égale à 1) en
, qui est la seule a avoir une valeur finie
(égale à 1) en
![]() . La solution élémentaire s'écrit (ligne 13)
. La solution élémentaire s'écrit (ligne 13)
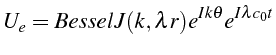
Cette solution élémentaire doit vérifier la condition à la limite
![]() en
en
![]() (ligne 14), ce qui
impose pour chaque valeur de
(ligne 14), ce qui
impose pour chaque valeur de
![]() des valeurs de
des valeurs de
![]() particulières.
Les valeurs possibles de
particulières.
Les valeurs possibles de
![]() sont les racines de la fonction
sont les racines de la fonction
![]() (ligne 16):
(ligne 16):
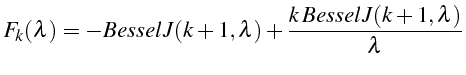
On a tracé cette fonction pour différentes valeur de k sur la figure
(4.8). Pour une valeur de
![]() fixé, on a une infinité de
racines
fixé, on a une infinité de
racines
![]() (c'est l'équivalent des racines
(c'est l'équivalent des racines
![]() des fonctions
des fonctions
![]() en coordonnées cartésiennes). La solution
élémentaire dépend donc de deux paramètres entiers
en coordonnées cartésiennes). La solution
élémentaire dépend donc de deux paramètres entiers
![]() et
et
![]() :
:
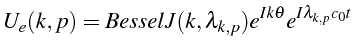
La solution générale de l'équation des ondes (4.12) est donc une combinaison linéaire de ces solutions élémentaires:
où
![]() est la
est la
![]() racine de
racine de
![]() .
Les coefficients
.
Les coefficients
![]() permettent à
permettent à
![]() de vérifier les
conditions initiales. A titre d'exemple, on a déterminé et tracé la
solution modale:
de vérifier les
conditions initiales. A titre d'exemple, on a déterminé et tracé la
solution modale:
pour les deux cas particuliers:
La discrétisation de l'équation des ondes (4.11) avec un
schéma explicite s'écrit en coordonnées cartésiennes sur un maillage
régulier de pas
![]() et
et
![]() :
:
C'est l'extension naturelle du schéma explicite 1D (c3eq15) du chapitre précédent.
Pour discrétiser l'équation en coordonnées polaires (4.15),
on discrétise le domaine polaire
![]() en
en
![]() avec un pas
avec un pas
![]() et
et
![]() , ce qui correspond à des points sur
des rayons et des cercles dans le domaine physique
, ce qui correspond à des points sur
des rayons et des cercles dans le domaine physique
![]() (figure
4.10). On note
(figure
4.10). On note
![]() et
et
![]() le nombre de noeuds
suivant
le nombre de noeuds
suivant
![]() et
et
![]()
En notant
![]() les valeurs aux noeuds,
la discrétisation par différences finies explicites de l'équation
(4.12) s'écrit:
les valeurs aux noeuds,
la discrétisation par différences finies explicites de l'équation
(4.12) s'écrit:
A cette équation, on ajoute la condition aux limites du problème (4.12)
en
![]() :
:
![]() . Pour imposer cette
condition, on utilise une condition miroir qui permet de calculer
la valeur inconnue
. Pour imposer cette
condition, on utilise une condition miroir qui permet de calculer
la valeur inconnue
![]() dans l'équation discrète sur
dans l'équation discrète sur
![]() :
:
A cette condition physique, il faut ajouter des conditions numériques liées à la transformation en coordonnées polaires:
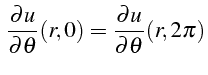
dans les équations pour
![]() et
et
![]() .
.
La seconde condition est nécessaire, car l'équation discrétisée (4.16)
dégénère en
![]() , de même que l'équation exacte (4.12)
à cause des termes en
, de même que l'équation exacte (4.12)
à cause des termes en
![]() .
.
Pour lever cette dégénérescence en
![]() , on utilise l'équation discrétisée
en coordonnées cartésiennes (4.15). Avec les notations de
la figure (4.11) et suivant les axes
, on utilise l'équation discrétisée
en coordonnées cartésiennes (4.15). Avec les notations de
la figure (4.11) et suivant les axes
![]() , cette équation
s'écrit en
, cette équation
s'écrit en
![]() :
:
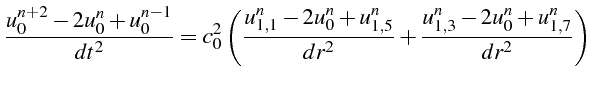
En effectuant une rotation des axes
![]() de 45 degrés, on obtiens
une autre équation équivalente:
de 45 degrés, on obtiens
une autre équation équivalente:
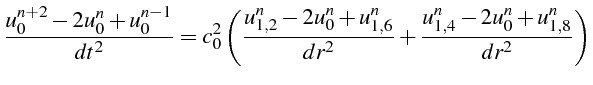
La valeur de
![]() étant unique, on choisit la moyenne de ces équations:
étant unique, on choisit la moyenne de ces équations:
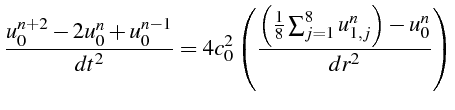
soit, de façon générale si on a
![]() noeuds dans la direction
noeuds dans la direction
![]() :
:
Cette dernière équation peut s'interpréter comme un bilan de flux
sur un disque de rayon
![]() . En intégrant l'équation (4.12)
sur ce disque, il vient, après utilisation du théorème de Green:
. En intégrant l'équation (4.12)
sur ce disque, il vient, après utilisation du théorème de Green:
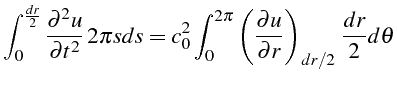
On approxime chacun de ses termes par différences finies. Pour le premier terme, on utilise l'approximation de la dérivée seconde en temps en
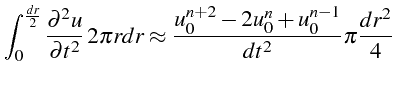
et pour le second l'approximation de la dérivée première en
![]() sur chaque rayon d'angle
sur chaque rayon d'angle
![]()
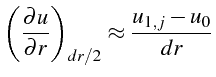
ce qui fournit l'approximation de la seconde intégrale:
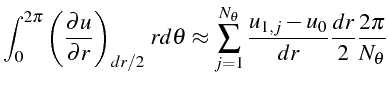
En combinant ces deux approximations, on retrouve l'équation (4.19),
qui permet de calculer l'évolution temporelle de la valeur
![]() .
.
La résolution numérique du schéma explicite (4.16) nécessite
l'initialisation de la solution
![]() à
à
![]() et
et
![]() à
à
![]() .
On applique la même démarche que pour l'équation des ondes en 1D (paragraphe
c3ondes). Disposant des deux conditions initiales du problème
(4.12), la valeur
.
On applique la même démarche que pour l'équation des ondes en 1D (paragraphe
c3ondes). Disposant des deux conditions initiales du problème
(4.12), la valeur
![]() est donnée par la première condition:
est donnée par la première condition:
et la valeur de
![]() est obtenue à partir d'un développement limité
en temps à l'ordre 2 autour de
est obtenue à partir d'un développement limité
en temps à l'ordre 2 autour de
![]() :
:
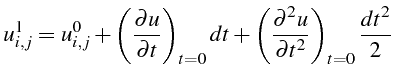
La valeur de
![]() est fournie par la seconde
condition initiale, et on utilise l'équation exacte pour calculer
est fournie par la seconde
condition initiale, et on utilise l'équation exacte pour calculer
![]() en fonction du laplacien de
en fonction du laplacien de
![]() , que l'on discrétise ensuite par différences finies centrées:
, que l'on discrétise ensuite par différences finies centrées:
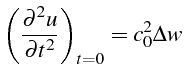
On obtiens ainsi la valeur de
![]() avec une précision
avec une précision
![]() ,
identique à celle du schéma:
,
identique à celle du schéma:
L'étude de la stabilité et de la consistance est effectuée tout d'abord sur l'équation discrétisée en coordonnées cartésiennes (4.15), et nous en déduirons ensuite les propriétés pour l'équation discrétisée en coordonnées polaires (4.16).
L'étude de la stabilité utilise le programme Maple 4.3.3.
On remplace (ligne 12) dans l'équation discrétisée définie à la ligne
7, la solution approchée
![]() par une perturbation, que
l'on a décomposé en mode de Fourier suivant
par une perturbation, que
l'on a décomposé en mode de Fourier suivant
![]() et
et
![]() (ligne 11):
(ligne 11):
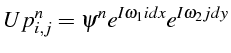
Après simplification, on obtiens une équation du second degré pour
le facteur d'amplification
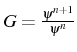 (ligne
19):
(ligne
19):
Le coefficient
![]() est simplifié (lignes 21 et 22), et s'exprime
en fonction de 2 nombres de Courant
est simplifié (lignes 21 et 22), et s'exprime
en fonction de 2 nombres de Courant
![]() et
et
![]() et de
et de
![]() et
et
![]() :
:
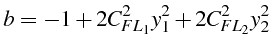
Le produit des racines de l'équation (4.22) étant égale à
1, la condition de stabilité
![]() impose donc que ces racines
soient complexes conjuguées, i.e. que le discriminant soit négatif:
impose donc que ces racines
soient complexes conjuguées, i.e. que le discriminant soit négatif:
![\bgroup\color{black}$\displaystyle \Delta=b^{2}-1\le0 \forall y_{1},y_{2}\in[-1,1]$\egroup](img1954.png)
ce qui conduit à la condition (ligne 25 et 26):
![\bgroup\color{black}$\displaystyle C_{FL_{1}}^{2}y_{1}^{2}+C_{FL_{2}}^{2}y_{2}^{2}\le1 \forall y_{1},y_{2}\in[-1,1]$\egroup](img1955.png)
La condition de stabilité du schéma explicite (4.15) s'écrit donc:
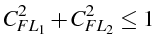
C'est une condition de Courant:
basé sur une longueur caractéristique
![]() de la maille différence
finie définie par:
de la maille différence
finie définie par:
Si les pas de discrétisation sont égaux (
![]() ), on a
), on a
![]() .
La condition de stabilité est donc plus sévère en 2D qu'en 1D.
.
La condition de stabilité est donc plus sévère en 2D qu'en 1D.
> restart;with(plots):
# Equation des ondes en cartesien
> diff(U(x,y,t),t$2)=c0^2*(diff(U(x,y,t),x$2)+
diff(U(x,y,t),y$2));
> eq:=%:
# Equation D.F.
> (U[i,j,n+1]-2*U[i,j,n]+U[i,j,n-1])/dt^2=c0^2*((U[i+1,j,n]-
2*U[i,j,n]+U[i-1,j,n])/dx^2+(U[i,j+1,n]-
2*U[i,j,n]+U[i,j-1,n])/dy^2); eqh:=%:
# Etude de stabilite
> Up:=(i,j,n)->Psi[n]*exp(I*omega[1]*i*dx)*exp(I*omega[2]*j*dy);
> subs(U[i,j,n+1]=Up(i,j,n+1),U[i,j,n-1]=Up(i,j,n-1),
U[i,j,n]=Up(i,j,n),U[i-1,j,n]=Up(i-1,j,n),
U[i+1,j,n]=Up(i+1,j,n),U[i,j-1,n]=Up(i,j-1,n),
U[i,j+1,n]=Up(i,j+1,n),eqh);
#
> rel1:=simplify(%*exp(-I*omega[1]*i*dx)*exp(-I*omega[2]*j*dy)):
> simplify(subs(Psi[n+1]=G*Psi[n],Psi[n-1]=Psi[n]/G,rel1*G/Psi[n]));
> collect(dt^2*(lhs(%)-rhs(%)),G)=0;eq3:=lhs(%):
# calcul du coefficient de G
> coeff(eq3,G):expand(%);
> subs(cos(omega[1]*dx)=1-2*y[1]^2,cos(omega[2]*dy)=1-2*y[2]^2,
dx=dt*c0/CFL[1],dy=dt*c0/CFL[2],%):simplify(%);b:=%/2;
# Racines G complexes conjuguees si Delta<0
> Delta:=b^2-1;factor(%);
> CFL[1]^2*y[1]^2+CFL[2]^2*y[2]^2<1;
# Condition de stabilite
> CFL[1]^2+CFL[2]^2<1;cdts:=%:
> subs(CFL[1]=c0*dt/dx,CFL[2]=c0*dt/dy,cdts);
> dt*c0*sqrt(1/dx^2+1/dy^2)<1;
# Erreur de troncature
> Uex:=(p,q,r)->U(x+(p-i)*dx,y+(q-j)*dy,t+(r-n)*dt);
> subs(U[i,j,n]=Uex(i,j,n),U[i,j,n-1]=Uex(i,j,n-1),U[i,j,n+1]=
Uex(i,j,n+1),U[i+1,j,n]=Uex(i+1,j,n),U[i-1,j,n]=Uex(i-1,j,n),
U[i,j+1,n]=Uex(i,j+1,n),U[i,j-1,n]=Uex(i,j-1,n),
lhs(eqh)-rhs(eqh)); rel3:=%:
#
> U(x,y,t+dt)=convert(mtaylor(U(x,y,t+dt),[dt],8),diff);S1:=%:
> U(x,y,t-dt)=convert(mtaylor(U(x,y,t-dt),[dt],8),diff):S2:=%:
> U(x+dx,y,t)=convert(mtaylor(U(x+dx,y,t),[dx],8),diff):S3:=%:
> U(x-dx,y,t)=convert(mtaylor(U(x-dx,y,t),[dx],8),diff):S4:=%:
> U(x,y+dy,t)=convert(mtaylor(U(x,y+dy,t),[dy],8),diff):S5:=%:
> U(x,y-dy,t)=convert(mtaylor(U(x,y-dy,t),[dy],8),diff):S6:=%:
> subs(S1,S2,S3,S4,S5,S6,rel3-(lhs(eq)-rhs(eq))):simplify(%);
# Schema d'ordre 2
Par analogie, la condition de stabilité du schéma explicite (4.16)
en coordonnée polaire est aussi la condition de Courant (4.23).
Il faut cependant définir la longueur caractéristique
![]() de la maille
en coordonnée polaire. Cette longueur ne doit pas être basée sur les
dimensions
de la maille
en coordonnée polaire. Cette longueur ne doit pas être basée sur les
dimensions
![]() et
et
![]() de la maille dans l'espace transformé,
mais sur les dimensions de la maille
de la maille dans l'espace transformé,
mais sur les dimensions de la maille
![]() et
et
![]() dans l'espace
physique:
dans l'espace
physique:
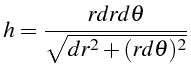
La maille dans l'espace physique n'étant pas constante (elle dépend
de
![]() ), on doit prendre la plus petite valeur de
), on doit prendre la plus petite valeur de
![]() dans le maillage,
qui est obtenue pour
dans le maillage,
qui est obtenue pour
![]()
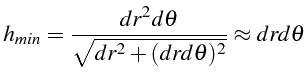
ce qui fournit la condition de stabilité du schéma (4.16):
On constate que cette condition en coordonnée polaire est beaucoup
plus contraignante que la condition (4.23) en coordonnées
cartésiennes. Pour un maillage de
![]() points dans chaque direction,
il faut choisir un pas en temps
points dans chaque direction,
il faut choisir un pas en temps
![]() tel que
tel que
![]() en cartésien et
en cartésien et
![]() en polaire.
en polaire.
Le calcul Maple (lignes 32 à 44 du programme 4.3.3) fournit l'erreur de troncature pour le schéma (4.15) en cartésien:
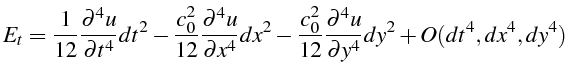
Le schéma explicite (4.15) est donc d'ordre 2 en temps et
en espace (i.e. a une précision en
![]() ).
).
Par analogie, on en déduit que le schéma explicite (4.16)
est aussi d'ordre 2 en temps et en espace (i.e. a une précision en
![]() ).
).
Enfin on note que ces schémas explicites (4.15) et (4.16)
sont des schémas dispersifs, mais non dissipatifs comme en 1D (puisque
le facteur d'amplification
![]() à un module égal à 1).
à un module égal à 1).
Le programme Matlab (4.3.4) implémente le schéma explicite
en cordonnées polaires (4.16). Les paramètres du calcul sont
définies sur les lignes 3 à 13, avec un
![]() définit par la relation
(4.25). Pour tenir compte simplement des conditions de périodicité,
la solution approchée
définit par la relation
(4.25). Pour tenir compte simplement des conditions de périodicité,
la solution approchée
![]() est définie comme un tableau
de dimension
est définie comme un tableau
de dimension
![]() , i.e. avec
, i.e. avec
![]() variant de
0
(
variant de
0
(
![]() à
à
![]()
![]() et
et
![]() de
0
de
0
![]() à
à
![]()
![]() . La solution initiale
. La solution initiale
![]() est définie sur les
lignes 14 à 21 comme combinaison linéaire des 2 modes propres (4.15).
Cette solution initiale permet l'initialisation des champs
est définie sur les
lignes 14 à 21 comme combinaison linéaire des 2 modes propres (4.15).
Cette solution initiale permet l'initialisation des champs
![]() (lignes 24 à 26). La seconde condition initiale (4.21) est
appliquée lors de la première itération en temps en notant que cette
condition est dans notre cas équivalente à l'équation aux différences
(4.16) pour
(lignes 24 à 26). La seconde condition initiale (4.21) est
appliquée lors de la première itération en temps en notant que cette
condition est dans notre cas équivalente à l'équation aux différences
(4.16) pour
![]() avec
avec
![]() , i.e.
l'équivalent d'une condition miroir à l'instant initiale. Cette condition
peut alors être implémentée en initialisant
, i.e.
l'équivalent d'une condition miroir à l'instant initiale. Cette condition
peut alors être implémentée en initialisant
![]() et
et
![]() avec
avec
![]() , et en calculant
, et en calculant
![]() à la première itération avec la
formule générale (4.16), et un coefficient
à la première itération avec la
formule générale (4.16), et un coefficient
![]() divisé
par deux (ligne 37).
divisé
par deux (ligne 37).
Dans les itérations en temps (lignes 34 à 57), on utilise l'équation
aux différences (4.16) pour les noeuds internes
![]() ,
,
![]() en utilisant la programmation matricielle Matlab
(ligne 40) . La condition aux limites en
en utilisant la programmation matricielle Matlab
(ligne 40) . La condition aux limites en
![]() fournit la valeur
aux noeuds frontières
fournit la valeur
aux noeuds frontières
![]() (ligne 45). Les conditions de périodicité
fournissent les valeurs aux noeuds frontières
(ligne 45). Les conditions de périodicité
fournissent les valeurs aux noeuds frontières
![]() et
et
![]() (lignes 49 à 50). Enfin l'équation pour les noeuds en
(lignes 49 à 50). Enfin l'équation pour les noeuds en
![]() est écrite
aux lignes 52 à 54.
est écrite
aux lignes 52 à 54.
% equation des ondes en polaire
% schema explicite
clear;
R1=1;
Ntheta=50; Nr=80;
dtheta=2*pi/(Ntheta-1);dr=R1/(Nr-1);
R=[0:dr:R1]';
Theta=[0:dtheta:2*pi];
% pts du maillage
X=R*cos(Theta); Y=R*sin(Theta);
% parametre
c0=1; CFL=0.9;
dt=CFL*dr*dtheta/c0
% cdts initial
k1=0; a1=1.0;
lambda1=fzero(inline('0*besselj(0,r)-r*besselj(1,r)'),10)
BJ1=inline('besselj(0,r)','r');
k2=1; a2=0.5;
lambda2=fzero(inline('1*besselj(1,r)-r*besselj(2,r)'),10)
BJ2=inline('besselj(1,r)','r');
W=(a1*BJ1(lambda1*R)*cos(k1*Theta)+...
a2*BJ2(lambda2*R)*cos(k2*Theta));
% initialisation
Un0=zeros(Nr,Ntheta+1);
Un0(:,1:Ntheta)=W; Un0(:,Ntheta+1)=Un0(:,2);
Un=Un0;Un1=Un;
% noeuds internes
I=[2:Nr-1];J=[2:Ntheta];
RI=R(I)*ones(1,Ntheta-1);
% schema D.F.
Tf=2*(2*pi/c0/lambda1);
nit=round(Tf/dt)
% iteration
for it=1:nit
coef=c0^2*dt^2;
if (it==1) coef=coef/2; end;
% noeuds internes
Un1(I,J)=2*Un(I,J)-Un0(I,J) + ...
(coef/dtheta^2)*(Un(I,J+1)-2*Un(I,J)+Un(I,J-1))./(RI.^2)+ ...
(coef/(2*dr))*(Un(I+1,J)-Un(I-1,J))./RI + ...
(coef/dr^2)*(Un(I+1,J)-2*Un(I,J)+Un(I-1,J));
% C.L. en r=1
Un1(Nr,J)=2*Un(Nr,J)-Un0(Nr,J) + ...
(coef/dtheta^2)*(Un(Nr,J+1)-2*Un(Nr,J)+Un(Nr,J-1))/(R(Nr))+ ...
(coef/dr^2)*(Un(Nr-1,J)-2*Un(Nr,J)+Un(Nr-1,J));
% periodicite
Un1(1:Nr,1)=Un1(1:Nr,Ntheta);
Un1(1:Nr,Ntheta+1)=Un1(1:Nr,2);
% C.L. en r=0
Um=sum(Un(2,2:Ntheta))/(Ntheta-1);
Um1=2*Un(1,1)-Un0(1,1)+(4*coef/dr^2)*(Um-Un(1,1));
Un1(1,1:Ntheta+1)=Um1;
% iteration suivante
Un0=Un; Un=Un1;
end;
Sur la figure (4.12), on a tracé la solution calculée au
bout d'une période, avec
![]() ,
,
![]() et
et
![]() ,
pour les deux conditions initiales étudiées analytiquement au paragraphe
sol_ondes2d. Elles se comparent parfaitement aux solutions
analytiques de la figure (4.9).
,
pour les deux conditions initiales étudiées analytiquement au paragraphe
sol_ondes2d. Elles se comparent parfaitement aux solutions
analytiques de la figure (4.9).
Pour tester la stabilité du schéma, nous avons fait varier le pas
en temps pour deux maillages donnés: (
![]() ,
,
![]() )
et (
)
et (
![]() ,
,
![]() ) avec la condition initiale suivante:
) avec la condition initiale suivante:
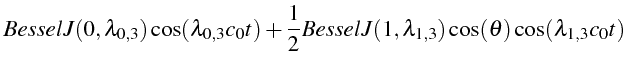
Nous avons ensuite calculé l'erreur en
![]() en comparant la solution
approchée sur l'axe
en comparant la solution
approchée sur l'axe
![]() et la solution exacte
et la solution exacte
![]() )
sur un temps
)
sur un temps
![]() de l'ordre de deux périodes
de l'ordre de deux périodes
![]() .
On a tracé ces évolutions sur la figure (4.13). On constate
bien que la solution diverge dès que le nombre de Courant (4.25)
est supérieur ou égale à 1. On peut aussi noter que si l'on choisit
une condition initiale ne dépendant pas de
.
On a tracé ces évolutions sur la figure (4.13). On constate
bien que la solution diverge dès que le nombre de Courant (4.25)
est supérieur ou égale à 1. On peut aussi noter que si l'on choisit
une condition initiale ne dépendant pas de
![]() la solution
reste stable pour des
la solution
reste stable pour des
![]() beaucoup plus grands (i.e.
beaucoup plus grands (i.e.
![]() ),
ce qui montre que l'instabilité la plus sévére proviens de la discrétisation
du terme en
),
ce qui montre que l'instabilité la plus sévére proviens de la discrétisation
du terme en
![]() . Théoriquement au bout d'un nombre très grand
d'itérations, les erreurs d'arrondis devraient pouvoir déstabiliser
la solution, mais ici la symétrie des calculs fait que ces erreurs
sont indépendantes de
. Théoriquement au bout d'un nombre très grand
d'itérations, les erreurs d'arrondis devraient pouvoir déstabiliser
la solution, mais ici la symétrie des calculs fait que ces erreurs
sont indépendantes de
![]() et la solution non perturbée reste
stable.
et la solution non perturbée reste
stable.
Pour étudier la précision du calcul, nous avons calculer l'erreur
au centre pour différents maillages avec un
![]() avec la
même condition initiale. La solution au centre étant indépendante
de
avec la
même condition initiale. La solution au centre étant indépendante
de
![]() , nous avons uniquement fait varier la discrétisation
suivant
, nous avons uniquement fait varier la discrétisation
suivant
![]() en choisissant des valeurs de
en choisissant des valeurs de
![]() de 10 à 640. La
taille caractéristique du maillage est
de 10 à 640. La
taille caractéristique du maillage est
![]() ,
et nous avons tracé l'erreur sur l'axe en fonction de
,
et nous avons tracé l'erreur sur l'axe en fonction de
![]() sur la
figure (4.14).
sur la
figure (4.14).
On constate sur cette figure que l'erreur se comporte à la limite
en
![]() , ce qui était prévue par la théorie. Cela montre que
notre condition en
, ce qui était prévue par la théorie. Cela montre que
notre condition en
![]() préserve la précision d'ordre 2 du schéma.
préserve la précision d'ordre 2 du schéma.