suivant: 4.3 Équation des ondes monter: 4. Schémas différences finies précédent: 4.1 Introduction Table des matières
On considère une membrane carrée de coté
![]() qui se déforme sous
l'effet d'une charge surfacique
qui se déforme sous
l'effet d'une charge surfacique
![]() . La membrane est sous tension
et fixée sur les bords. On suppose qu'en chacun des points la tension
. La membrane est sous tension
et fixée sur les bords. On suppose qu'en chacun des points la tension
![]() est constante et tangente à la membrane (on néglige les forces
élastiques dues à la déformation de la membrane). On note
est constante et tangente à la membrane (on néglige les forces
élastiques dues à la déformation de la membrane). On note
![]() la déformée. Les forces exercées sur un élément de membrane
la déformée. Les forces exercées sur un élément de membrane
![]()
![]() sont:
sont:
![$\displaystyle Tdy\left[\begin{array}{c}
-\cos\theta_{x}\\
0\\
\sin\theta_{x}\end{array}\right]$](img1722.png)
en notant
![$\displaystyle Tdx\left[\begin{array}{c}
0\\
-\cos\theta_{y}\\
\sin\theta_{y}\end{array}\right]$](img1724.png)
| 0 | |||
| 0 | |||
avec
![]() et
et
![]() .
En supposant que les angles
.
En supposant que les angles
![]() sont petits, i.e:
sont petits, i.e:
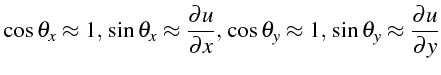
On effectue des développements limités à l'ordre 1 dans les équations précédentes, qui conduisent à l'équation d'équilibre de la membrane:
auquel on ajoute les conditions aux limites:
En effectuant un changement de variables, on obtiens le problème modèle suivant, qui est une équation de Poisson:
| (4.2) | |
Pour déterminer la solution générale de l'équation de Poisson (4.2),
on décompose
![]() en série de Fourier vérifiant les conditions
aux limites:
en série de Fourier vérifiant les conditions
aux limites:
En remplaçant dans (4.2), on obtiens:
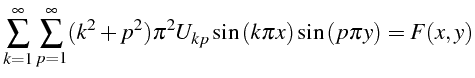
d'où les valeurs de
![]() , en multipliant cette relation par
, en multipliant cette relation par
![]() .
En intégrant sur le domaine
.
En intégrant sur le domaine
![]() et en utilisant l'orthogonalité
des fonctions
et en utilisant l'orthogonalité
des fonctions
![]() , il vient:
, il vient:
Dans le cas d'un chargement constant
![]() , la valeur du coefficient
de Fourier
, la valeur du coefficient
de Fourier
![]() se calcule simplement avec Maple et on trouve:
se calcule simplement avec Maple et on trouve:
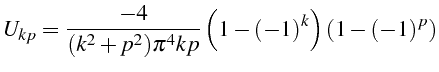
Ce coefficient est non nul si et seulement si
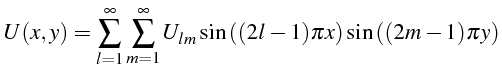 |
|
avec 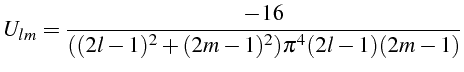 |
L'allure de la solution est donnée sur la figure (4.2).
La valeur maximale
![]() de la déformation se trouve au centre
et a pour expression:
de la déformation se trouve au centre
et a pour expression:
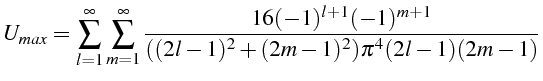
On peut calculer une valeur approchée très précise de cette série
avec Maple, et on trouve (pour
![]() ):
):
Sur un maillage de
![]() points suivant
points suivant
![]() et
et
![]() points
suivant
points
suivant
![]() (figure 4.3), la discrétisation par différences
finies centrées de l'équation (4.2) s'écrit:
(figure 4.3), la discrétisation par différences
finies centrées de l'équation (4.2) s'écrit:
avec les conditions aux limites:
Les pas de discrétisation en espace sont équidistants et vérifient
![]() et
et
![]() .
.
Ce schéma conduit à un système matriciel de
![]() inconnues
inconnues
![]() . Pour écrire ce système sous la forme matricielle
. Pour écrire ce système sous la forme matricielle
![]() ,
on doit transformer la matrice des inconnues
,
on doit transformer la matrice des inconnues
![]() en un vecteur
inconnu
en un vecteur
inconnu
![]() . Pour cela on numérote les inconnues par lignes,
i.e. on effectue la transformation d'indice
. Pour cela on numérote les inconnues par lignes,
i.e. on effectue la transformation d'indice
![]() vers le mono-indice
vers le mono-indice
![]() . Avec ce changement d'indice, l'équation aux différences
(4.6) s'écrit:
. Avec ce changement d'indice, l'équation aux différences
(4.6) s'écrit:
pour tous les noeuds internes
Les conditions aux limites s'écrivent
![]() pour les noeuds frontières
pour les noeuds frontières
![]() ,
,
![]() avec
avec
![]() et
et
![]() ,
,
![]() avec
avec
![]() .
.
La matrice
![]() est une matrice penta-diagonale dont la
forme est donnée sur la figure (4.4a). On vérifie que la
matrice possède bien au maximum 5 coefficients non nuls répartis sur
la diagonale de coefficients
est une matrice penta-diagonale dont la
forme est donnée sur la figure (4.4a). On vérifie que la
matrice possède bien au maximum 5 coefficients non nuls répartis sur
la diagonale de coefficients
![]() , les 2 co-diagonales adjacentes
de coefficients
, les 2 co-diagonales adjacentes
de coefficients
![]() et les 2 co-diagonales distantes de
et les 2 co-diagonales distantes de
![]() de la diagonale de coefficients
de la diagonale de coefficients
![]() . On constate aussi que la matrice
. On constate aussi que la matrice
![]() est non symétrique, à cause de la façon d'appliquer
les conditions aux limites. En effet pour un noeud
est non symétrique, à cause de la façon d'appliquer
les conditions aux limites. En effet pour un noeud
![]() sur la frontière,
on applique la condition aux limites
sur la frontière,
on applique la condition aux limites
![]() dans la ligne
dans la ligne
![]() de la matrice en annulant la ligne et en mettant
de la matrice en annulant la ligne et en mettant
![]() sur la diagonale.
On ne tiens pas compte de cette condition aux limites dans les équations
où intervient la valeur de
sur la diagonale.
On ne tiens pas compte de cette condition aux limites dans les équations
où intervient la valeur de
![]() , i.e. dans les lignes de
, i.e. dans les lignes de
![]() ayant un coefficient non nul dans la colonne
ayant un coefficient non nul dans la colonne
![]() . Pour conserver
la symétrie de la matrice, qui traduit la symétrie du problème physique,
il faut aussi annuler les coefficients de la colonne
. Pour conserver
la symétrie de la matrice, qui traduit la symétrie du problème physique,
il faut aussi annuler les coefficients de la colonne
![]() (figure
4.4b). Dans le cas
(figure
4.4b). Dans le cas
![]() , il faut en outre retrancher
la colonne
, il faut en outre retrancher
la colonne
![]() du second membre
du second membre
![]() .
.
On note aussi que le nombre de coefficients non nuls de la matrice
![]() est de l'ordre de
est de l'ordre de
![]() , ce qui
est beaucoup plus petit que le nombre de coefficients
, ce qui
est beaucoup plus petit que le nombre de coefficients
![]() de la matrice
de la matrice
![]() . On tiendra compte de ces propriétés
lors de la résolution du système matriciel.
. On tiendra compte de ces propriétés
lors de la résolution du système matriciel.
On utilise une discrétisation centrée et d'ordre 2 de la dérivée seconde
en
![]() et en
et en
![]() , donc l'erreur de troncature du schéma est d'ordre
, donc l'erreur de troncature du schéma est d'ordre
![]() . Elle s'écrit:
. Elle s'écrit:
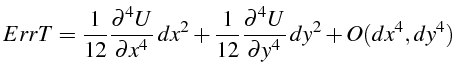
La précision du schéma (4.6) est donc d'ordre 2 en espace,
i.e. en
![]() .
.
La fonction Matlab laplace2d (4.2.4) calcule la
matrice
![]() et le second membre
et le second membre
![]() sur un maillage
différences finis de
sur un maillage
différences finis de
![]() points pour une fonction
points pour une fonction
![]() définie
aux noeuds
définie
aux noeuds
![]() du maillage et des conditions aux limites homogènes.
Compte tenu des remarques sur la structure de la matrice
du maillage et des conditions aux limites homogènes.
Compte tenu des remarques sur la structure de la matrice
![]() ,
on utilise une structure de donnée de matrice creuse (sparse
matrix en anglais) qui permet de ne stocker que les éléments non
nuls. Pour cela on stocke les coefficients non nuls de
,
on utilise une structure de donnée de matrice creuse (sparse
matrix en anglais) qui permet de ne stocker que les éléments non
nuls. Pour cela on stocke les coefficients non nuls de
![]() dans un vecteur Ac, ainsi que leurs indices (i,j)
dans deux autres vecteurs I et J. Pour la matrice
dans un vecteur Ac, ainsi que leurs indices (i,j)
dans deux autres vecteurs I et J. Pour la matrice
![]() ci dessous:
ci dessous:
![\bgroup\color{black}$\displaystyle \mathcal{A}=\left[\begin{array}{ccccc}
4 & -1...
...4 & -1 & 0\\
0 & 0 & -1 & 4 & 0\\
-1 & 0 & 0 & 0 & 4\end{array}\right]$\egroup](img1791.png)
on utilise les 3 tableaux suivants:
function [A,B]=laplace2d(F,nx,ny)
% entree:
% matrice F du second membre Fij valeur de F au noeud (i,j)
% nx,ny nombre de points en x et en y
% sortie:
% matrice A et second membre B
% en utilisant un stocage creux
% pble -lap(U)=f avec des C.L. homogene
dx=1/(nx-1); dy=1/(ny-1);
% coefficiant du shema pour les nds
% (i,j-1) (i-1,j) (i,j) (i+1,j) (i,j+1)
coeff=[-1/dy^2,-1/dx^2,2/dx^2+2/dy^2,-1/dx^2,-1/dy^2];
% decalage / au neud (i,j) dans la numérotation
num = [ -nx, -1, 0, 1, nx];
% assemblage de la matrice pour un stocage par ligne
% i.e le noeud (i,j) a pour adresse k=(j-1)*nx+i
N=nx*ny; % dimension
A=spalloc(N,N,5*N); % matrice creuse de 5 elts maxi / ligne
B=reshape(F,N,1);
for i=2:nx-1
for j=2:ny-1
k=(j-1)*nx+i;
A(k,k+num)=coeff;
end
end
% conditions aux limites
% ======================
% C.L. sur les frontieres i=1,i=nx (Dirichlet)
for j=1:ny
k=(j-1)*nx+1; A(k,:)=0; A(:,k);A(k,k)=1.0; B(k)=0;
k=(j-1)*nx+nx; A(k,:)=0; A(:,k)=0; A(k,k)=1.0; B(k)=0;
end;
% C.L. sur les frontieres j=1,j=ny (Dirichlet)
for i=1:nx
k=i; A(k,:)=0; A(:,k)=0; A(k,k)=1.0; B(k)=0;
k=(ny-1)*nx+i; A(k,:)=0; A(:,k)=0; A(k,k)=1.0; B(k)=0;
end;
% fin
Pour le second membre
![]() on transforme la matrice
on transforme la matrice
![]() des valeurs aux noeuds du maillage en un vecteur de colonne de dimension
des valeurs aux noeuds du maillage en un vecteur de colonne de dimension
![]() avec la fonction Matlab reshape. La boucle d'assemblage
de
avec la fonction Matlab reshape. La boucle d'assemblage
de
![]() correspond aux lignes 20 à 25, et se fait ligne
par ligne en utilisant la structure matricielle de Matlab (ligne 23).
Les conditions aux limites sont imposées sur les cotés
correspond aux lignes 20 à 25, et se fait ligne
par ligne en utilisant la structure matricielle de Matlab (ligne 23).
Les conditions aux limites sont imposées sur les cotés
![]() et
et
![]() (lignes 29 à 32) et
(lignes 29 à 32) et
![]() et
et
![]() (lignes 34 à 37), en annulant
la ligne et la colonne
(lignes 34 à 37), en annulant
la ligne et la colonne
![]() de
de
![]() ainsi que le second
membre
ainsi que le second
membre
![]() puis en imposant
puis en imposant
![]() .
.
Le script Matlab (4.2.4) résout numériquement le problème
(4.2) dans le cas d'une fonction
![]() (ligne 8). On utilise
la fonction Laplace2d précédente pour calculer la matrice
(ligne 8). On utilise
la fonction Laplace2d précédente pour calculer la matrice
![]() et le second membre
et le second membre
![]() du problème. On
résout le système (ligne 11) avec l'opérateur standard
du problème. On
résout le système (ligne 11) avec l'opérateur standard
![]() de Matlab, qui pour des matrices creuses utilisent un algorithme de
Gauss par bande. C'est la méthode la plus efficace sous Matlab, même
si elle nécessite un stockage temporaire important, de l'ordre de
de Matlab, qui pour des matrices creuses utilisent un algorithme de
Gauss par bande. C'est la méthode la plus efficace sous Matlab, même
si elle nécessite un stockage temporaire important, de l'ordre de
![]() puisque la largeur de bande vaut
puisque la largeur de bande vaut
![]() . En utilisant
la structure particulière de la matrice
. En utilisant
la structure particulière de la matrice
![]() (tri-diagonale
par blocs), on pourrait utiliser un algorithme très efficace, qui
est l'extension de l'algorithme de Thomas. Son principe est décrit
dans l'annexe 3DBloc, mais il n'est pas implémenté sous Matlab.
(tri-diagonale
par blocs), on pourrait utiliser un algorithme très efficace, qui
est l'extension de l'algorithme de Thomas. Son principe est décrit
dans l'annexe 3DBloc, mais il n'est pas implémenté sous Matlab.
La fin du script permet la visualisation en 3D de la solution calculée.
% resolution du laplacien
clear
% dimension
nx=21; ny=21;
dx=1/(nx-1); dy=1/(ny-1);
X=[0:dx:1]; Y=[0:dy:1];
% assemblage matrice et 2nd membre
F=-ones(nx,ny);
[A,B]=laplace2d(F,nx,ny);
% resolution
U=A\B;
% transformation de U en matrice pour visualisation
U1=reshape(U,nx,ny);
% visualisation
surfc(X,Y,U1); title('deformee'); shading interp;
On a tracé le résultat obtenu pour
![]() sur la figure
(4.5). En comparant avec la solution exacte (figure 4.2),
on constate une bonne concordance. L'erreur relative sur la valeur
maximale de la déformée est inférieure à 3%:
sur la figure
(4.5). En comparant avec la solution exacte (figure 4.2),
on constate une bonne concordance. L'erreur relative sur la valeur
maximale de la déformée est inférieure à 3%:
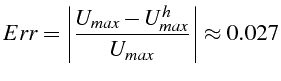
où on a noté
![]() la valeur exacte (4.5) et
la valeur exacte (4.5) et
![]() est la valeur approchée.
est la valeur approchée.
Pour terminer cette étude, nous avons effectué une étude de précision
en calculant cette erreur relative pour différents maillages (avec
un nombre de points identique suivant
![]() et
et
![]() ). Chaque maillage
est caractérisée par un pas de discrétisation
). Chaque maillage
est caractérisée par un pas de discrétisation
![]() . Sur la figure
(4.6), on a tracé l'évolution de l'erreur relative
. Sur la figure
(4.6), on a tracé l'évolution de l'erreur relative
![]() en fonction de
en fonction de
![]() , et on trouve sur une échelle logarithmique une
droite de pente 2. Cela montre que l'erreur relative est en
, et on trouve sur une échelle logarithmique une
droite de pente 2. Cela montre que l'erreur relative est en
![]() ,
ce qui confirme le calcul de l'erreur de troncature en
,
ce qui confirme le calcul de l'erreur de troncature en
![]() .
.