suivant: 3.6 Equation de transport monter: 3. Étude de schémas précédent: 3.4 Équation de convection-diffusion Table des matières
On considère la propagation d'une onde sonore plane dans tube de longueur
![]() contenant un milieu au repos de densité
contenant un milieu au repos de densité
![]() et de pression
et de pression
![]() . Le milieu est perturbé à l'instant initial par une fluctuation
de pression
. Le milieu est perturbé à l'instant initial par une fluctuation
de pression
![]() ne dépendant que de la direction spatiale
ne dépendant que de la direction spatiale
![]() et sans vitesse initiale (i.e.
et sans vitesse initiale (i.e.
![]() ).
La densité
).
La densité
![]() , la pression
, la pression
![]() et la
vitesse
et la
vitesse
![]() du milieu perturbée sont solutions des équations
de conservation d'Euler, qui décrivent la dynamique d'un gaz non visqueux.
En supposant que les perturbations sont faibles (hypothèse de l'acoustique),
l'équation de conservation de la masse s'écrit au premier ordre:
du milieu perturbée sont solutions des équations
de conservation d'Euler, qui décrivent la dynamique d'un gaz non visqueux.
En supposant que les perturbations sont faibles (hypothèse de l'acoustique),
l'équation de conservation de la masse s'écrit au premier ordre:
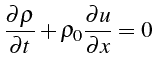
De même l'équation de conservation de la quantité de mouvement s'écrit au premier ordre:
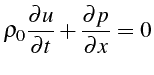
Les fluctuations étant faibles, on peut supposer l'écoulement isentropique, i.e.:
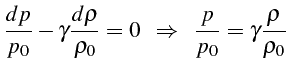
De ces relations on en déduit un système d'équations hyperbolique
sur
![]() et
et
![]() :
:
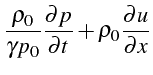 |
0 | ||
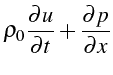 |
0 |
En dérivant la première équation par rapport à t et la seconde par
rapport à x, on obtiens par différence l'équation des ondes pour la
fluctutation de pression
![]() :
:
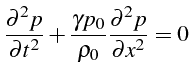
Si les deux extrémités du tube sont ouvertes, on peut considérer que
la pression y est constante et égale à
![]() . La fluctuation de
pression vérifie alors une condition de Dirichlet homogène
. La fluctuation de
pression vérifie alors une condition de Dirichlet homogène
![]() en
en
![]() et
et
![]() . Dans le cas d'extrémités fermés (parois solides),
la fluctuation de vitesse y est nulle, et la fluctuation de pression
vérifie une condition de Neumann
. Dans le cas d'extrémités fermés (parois solides),
la fluctuation de vitesse y est nulle, et la fluctuation de pression
vérifie une condition de Neumann
![]() en
en
![]() et
et
![]() (car
(car
![]() si
si
![]() ).
).
Pour un tube ouvert, la fluctuation de pression
![]() est solution
de l'équation des ondes, avec les conditions aux limites et initiales
suivantes:
est solution
de l'équation des ondes, avec les conditions aux limites et initiales
suivantes:
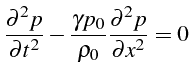 |
|
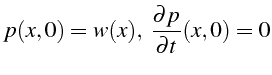 |
Cette équation décrit la propagation d'ondes de pression avec une
célérité
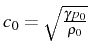 . Le problème
modèle associé s'écrit:
. Le problème
modèle associé s'écrit:
En effectuant le changement de variables
![]() et
et
![]() ,
l'équation (3.45) s'écrit:
,
l'équation (3.45) s'écrit:
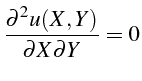
dont la solution est
![]() . La solution générale
. La solution générale
![]() de l'équation des ondes (3.45) s'écrit:
de l'équation des ondes (3.45) s'écrit:
qui est la somme d'une onde progressive
![]() qui se propage avec la
célérité
qui se propage avec la
célérité
![]() et d'une onde régressive
et d'une onde régressive
![]() qui se propage avec
la célérité
qui se propage avec
la célérité
![]() . Les fonctions
. Les fonctions
![]() et
et
![]() sont déterminées
par les conditions initiales et aux limites du problème. Nous étudierons
plus particulièrement les deux cas suivants:
sont déterminées
par les conditions initiales et aux limites du problème. Nous étudierons
plus particulièrement les deux cas suivants:
On suppose que la perturbation à l'instant initiale est un créneau
de largeur
![]() centré en
centré en
![]() , qui peut être définie mathématiquement
sous la forme:
, qui peut être définie mathématiquement
sous la forme:
Les fonctions
![]() et
et
![]() doivent donc vérifier à l'instant initial
les deux équations:
doivent donc vérifier à l'instant initial
les deux équations:
dont les solutions, à une constante additive près, s'écrivent:
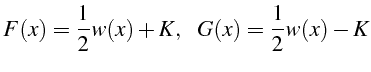
La solution
![]() :
:
décrit la propagation dans des directions opposées de deux créneaux
de hauteur égale à la moitié de la hauteur initiale. Cette solution
vérifie les conditions aux limites tant que les créneaux n'ont pas
atteint les frontières, i.e. pour
![]() . Lorsque le
créneau sort du domaine à
. Lorsque le
créneau sort du domaine à
![]() , la solution (3.46)
ne vérifie plus les conditions aux limites puisque
, la solution (3.46)
ne vérifie plus les conditions aux limites puisque
![]() et
et
![]() . Pour que ces conditions soient
vérifiées, il faut qu'une autre onde
. Pour que ces conditions soient
vérifiées, il faut qu'une autre onde
![]() de signe opposé
rentre dans le domaine en
de signe opposé
rentre dans le domaine en
![]() et
et
![]() , de telle sorte que
, de telle sorte que
![]() et
et
![]() . Cela correspond à la réflexion de l'onde
initiale sur la frontière. Cette onde entrante s'écrit:
. Cela correspond à la réflexion de l'onde
initiale sur la frontière. Cette onde entrante s'écrit:
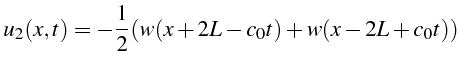
Elle correspond à la propagation de deux ondes d'amplitude
![]() qui traversent le domaine et ressortent à
qui traversent le domaine et ressortent à
![]() .
A nouveau pour que la solution vérifie les conditions aux limites,
il faut qu'une onde
.
A nouveau pour que la solution vérifie les conditions aux limites,
il faut qu'une onde
![]() de signe opposé rentre dans le domaine.
Cette onde s'écrit:
de signe opposé rentre dans le domaine.
Cette onde s'écrit:
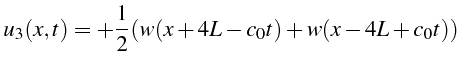
Elle correspond à la propagation de 2 ondes d'amplitude
![]() ,
qui traversent le domaine et qui à
,
qui traversent le domaine et qui à
![]() se rencontrent pour reformer l'onde initiale
se rencontrent pour reformer l'onde initiale
![]() . Le processus
est ensuite périodique.
. Le processus
est ensuite périodique.
La solution
![]() est donc une solution périodique, de période
est donc une solution périodique, de période
![]() , qui correspond à la somme de ces 3 ondes
pour
, qui correspond à la somme de ces 3 ondes
pour
![]() :
:
On a tracé sur la figure (3.23) l'évolution temporelle de cette solution sur une période. On observe bien la réflexion des ondes sur les parois du domaine.
Le programme Maple (3.5.2) permet de tracer l'animation temporelle de cette solution en utilisant la fonction Maple animate.
> restart: with(plots): # Solution exacte equation des ondes: cas 1 > delta:=1/10; > w:=x->Heaviside(x+delta)*Heaviside(delta-x); > u(t,x)=1/2*(w(x-c0*t)+w(x+c0*t))-1/2*(w(x+2*L-c0*t)+ w(x-2*L+c0*t))+1/2*(w(x+4*L-c0*t)+w(x-4*L+c0*t));sol:=rhs(%): > animate(subs(c0=1,L=1,sol),x=-1..1,t=0..4,numpoints=200,frames=100); # Solution exacte equation des ondes: cas 2 > m:=3;Tf:=4*L/c0/(2*m+1); > u(t,x)=cos((2*m+1)*Pi/2*x/L)*cos((2*m+1)*Pi/2*c0/L*t);sol:=rhs(%): > animate(subs(c0=1,L=1,sol),x=-1..1,t=0..4/7,numpoints=200,frames=100);
Dans le cas d'une solution initiale harmonique, i.e. de période multiple
de
![]() :
:
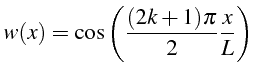
la solution s'écrit d'après (3.46):
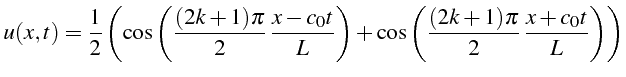
qui après transformation trigonométrique donne:
C'est une onde stationnaire de période
![]() ,
dont on a tracé la représentation sur la figure (3.24)
pour
,
dont on a tracé la représentation sur la figure (3.24)
pour
![]() . Le programme Maple (3.5.2) permet de tracer
l'animation temporelle de cette solution.
. Le programme Maple (3.5.2) permet de tracer
l'animation temporelle de cette solution.
On peut montrer, en utilisant la méthode de séparation de variables, que la solution générale de l'équation des ondes (3.45) est une combinaison linéaire d'ondes stationnaires:
Les coefficients
![]() sont alors les coefficients de Fourier de
la solution initiale
sont alors les coefficients de Fourier de
la solution initiale
![]() . Ainsi la solution du créneau (3.47)
peut aussi s'écrire sous la forme d'une combinaison d'ondes stationnaires
(3.49), mais dans ce cas le nombre d'ondes stationnaires
à considérer est très grands (infinie en théorie), car la série de
Fourier associée converge très lentement.
. Ainsi la solution du créneau (3.47)
peut aussi s'écrire sous la forme d'une combinaison d'ondes stationnaires
(3.49), mais dans ce cas le nombre d'ondes stationnaires
à considérer est très grands (infinie en théorie), car la série de
Fourier associée converge très lentement.
La discrétisation de l'équation des ondes (3.45) par un schéma de différences finies explicite centré s'écrit:
C'est un schéma explicite qui donne la valeur inconnue
![]() à l'étape
à l'étape
![]() en fonction des valeurs connues
en fonction des valeurs connues
![]() à l'étape
à l'étape
![]() et
et
![]() comme indiqué sur le diagramme (3.25).
comme indiqué sur le diagramme (3.25).
L'étude de la stabilité se fait classiquement avec la méthode de perturbation
de Neumann. L'évolution temporelle d'un mode de Fourier d'une perturbation
![]() vérifie l'équation
aux différences, soit après simplification par
vérifie l'équation
aux différences, soit après simplification par
![]() :
:
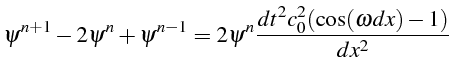
En notant
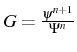 le facteur d'amplification
du schéma, la relation de récurrence à 2 niveaux précédente conduit
à l'équation du second degré suivante:
le facteur d'amplification
du schéma, la relation de récurrence à 2 niveaux précédente conduit
à l'équation du second degré suivante:
dans laquelle on a introduit le nombre de Courant
![]() :
:
Le mode de Fourier
![]() est donc une combinaison
linéaire des racines
est donc une combinaison
linéaire des racines
![]() et
et
![]() de cette équation (3.51):
de cette équation (3.51):
Si cette perturbation ne croît pas au cours du temps, le schéma est stable. Il faut donc:
D'après l'équation (3.51), le produit des racines
![]() est égal à
est égal à
![]() . Donc si les racines sont réelles, l'une des racines
est en module supérieure à
. Donc si les racines sont réelles, l'une des racines
est en module supérieure à
![]() et le schéma est instable. Par contre
si les racines sont complexes conjuguées, leur module est égale à
1 et le schéma est stable. Pour que l'équation (3.51) ait
des racines complexes, il faut que son discriminant soit négatif,
i.e. que:
et le schéma est instable. Par contre
si les racines sont complexes conjuguées, leur module est égale à
1 et le schéma est stable. Pour que l'équation (3.51) ait
des racines complexes, il faut que son discriminant soit négatif,
i.e. que:
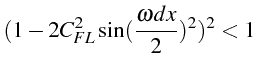
soit:
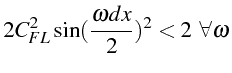
ce qui conduit à la condition classique de Courant:
Le schèma explicite est donc conditionnellement stable avec une condition de stabilité donnée par la condition de Courant (3.54).
Pour étudier la consistance de ce schéma, nous utiliserons le programme Maple (3.5.3).
> restart;with(plots):
# Etude de l'equation des ondes
> diff(U(t,x),t$2)-c0^2*diff(U(t,x),x$2)=0;eq:=%:
# Schema discret D.F.
> (U[n+1,i]-2*U[n,i]+U[n-1,i])/dt^2=
c0^2*(U[n,i+1]-2*U[n,i]+U[n,i-1])/dx^2; eqh:=%:
# Consistance
> Uex:=(p,q)->U(t+(p-n)*dt,x+(q-i)*dx);
> subs(U[n,i]=Uex(n,i),U[n-1,i]=Uex(n-1,i),
U[n,i+1]=Uex(n,i+1),U[n,i-1]=Uex(n,i-1),
U[n+1,i]=Uex(n+1,i),lhs(eqh)-rhs(eqh)); rel3:=%:
> expand(simplify(rel3-lhs(eq)));rel4:=%:
# Develt en serie de Taylor
> U(t+dt,x)=convert(mtaylor(U(t+dt,x),[dt],6),diff);S1:=%:
> U(t-dt,x)=convert(mtaylor(U(t-dt,x),[dt],6),diff):S2:=%:
> U(t,x+dx)=convert(mtaylor(U(t,x+dx),[dx],6),diff):S3:=%:
> U(t,x-dx)=convert(mtaylor(U(t,x-dx),[dx],6),diff):S4:=%:
# Erreur de tronacture
> simplify(subs(S1,S2,S3,S4,rel4));
> ErrT:=collect(%,dt);
# transformation a l'aide de l'equation
> eq;diff(U(t,x),t$4)=c0^4*diff(U(t,x),x$4);
> simplify(subs(%,ErrT));
Le programme fournit l'erreur de troncature suivante:
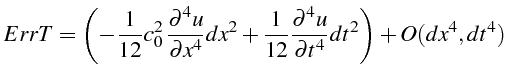
que l'on peut transformer en dérivant 2 fois l'équation (3.45), et en introduisant le nombre de Courant (3.52):
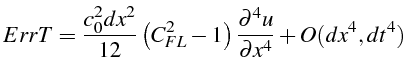
Le schéma explicite est donc consistant à l'équation des ondes. Il est d'ordre 2 en espace et en temps.
On peut montrer que pour la valeur particulière
![]() , l'erreur
de troncature est exactement nulle, et la solution exacte est alors
solution de l'équation discrète. Pour
, l'erreur
de troncature est exactement nulle, et la solution exacte est alors
solution de l'équation discrète. Pour
![]() (limite de stabilité),
le schéma explicite fournit donc la solution exacte de l'équation
des ondes.
(limite de stabilité),
le schéma explicite fournit donc la solution exacte de l'équation
des ondes.
D'après ce calcul d'erreur de troncature, l'équation aux différences finies (3.50) est donc équivalente à l'équation suivante:
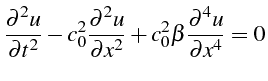
avec un coefficient
![]() égal à :
égal à :
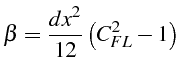
C'est une équation d'ondes avec dispersion dont la solution élémentaire s'écrit:
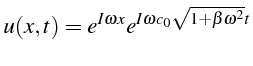
Cette solution correspond à la propagation d'une onde avec une célérité
![]() fonction de la pulsation
fonction de la pulsation
![]() .
Dans notre cas
.
Dans notre cas
![]() est négatif (car
est négatif (car
![]() ) et les
ondes hautes fréquences sont donc ralenties par le schéma numérique.
) et les
ondes hautes fréquences sont donc ralenties par le schéma numérique.
Pour étudier les propriétés de la solution approchée, nous allons
utiliser la même démarche que dans le paragraphe c3disp. Pour
cela nous allons considérer le problème de la convection d'une onde
![]() , vérifiant les conditions aux limites (i.e.
avec
, vérifiant les conditions aux limites (i.e.
avec
![]() ). La solution exacte de l'équation
des ondes (3.45) s'écrit:
). La solution exacte de l'équation
des ondes (3.45) s'écrit:
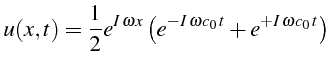
Cette solution initiale correspond justement à la perturbation
![]() dans la méthode de stabilité de Neumann. La solution numérique
dans la méthode de stabilité de Neumann. La solution numérique
![]() peut dans ce cas se calculer à partir de la relation (3.53).
Elle s'écrit en fonction de la solution initiale
peut dans ce cas se calculer à partir de la relation (3.53).
Elle s'écrit en fonction de la solution initiale
![]() au noeud
au noeud
![]() du maillage :
du maillage :
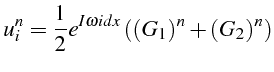
![]() et
et
![]() sont les 2 racines complexes de l'équation 3.51:
sont les 2 racines complexes de l'équation 3.51:
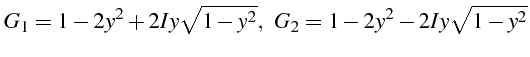
en notant
![]() . Ce sont deux nombres
complexes conjugués de module unité et de phase
. Ce sont deux nombres
complexes conjugués de module unité et de phase
![]() :
:
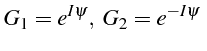 avec
avec 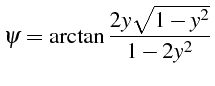
La solution discrète
![]() s'écrit sous la forme:
s'écrit sous la forme:
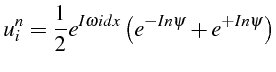
qu'il faut comparer à la solution exacte:
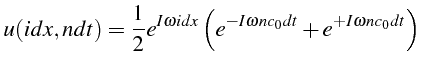
Ces deux expressions décrivent la propagation de l'onde initiale:
la première avec la célérité
![]() et la seconde
avec la célérité
et la seconde
avec la célérité
![]() .
.
En effectuant un développement limité de
![]() par rapport à
par rapport à
![]() ,
on montre que:
,
on montre que:
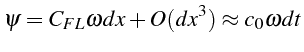
La solution approchée converge vers la solution exacte à l'ordre 2.
L'erreur entre la solution exacte et la solution approchée provient
essentiellement d'une erreur de dispersion: i.e. la solution numérique
se propage sans dissipation, mais avec une célérité légèrement différente
de la célérité exacte
![]() . Nous avons tracé sur la figure (3.26)
la célérité (multipliée par
. Nous avons tracé sur la figure (3.26)
la célérité (multipliée par
![]() ) de l'onde pour la solution
exacte et la solution approchée en fonction de la pulsation
) de l'onde pour la solution
exacte et la solution approchée en fonction de la pulsation
![]() .
On note que pour les petits nombres d'ondes (i.e. les basses fréquences)
l'écart est minime, et que cet écart croit avec le nombre d'onde (i.e
avec la fréquence).
.
On note que pour les petits nombres d'ondes (i.e. les basses fréquences)
l'écart est minime, et que cet écart croit avec le nombre d'onde (i.e
avec la fréquence).
La dispersion numérique du schéma augmente donc avec la fréquence.
Les ondes hautes fréquences sont ralenties par le schéma numérique
puisque leur célérité est plus petite que
![]() , comme prédit par
l'analyse de consistance.
, comme prédit par
l'analyse de consistance.
La résolution numérique du schéma explicite (3.50) nécessite
l'initialisation de la solution
![]() à
à
![]() et
et
![]() à
à
![]() .
Disposant de deux conditions initiales (3.45), la valeur
.
Disposant de deux conditions initiales (3.45), la valeur
![]() est donnée par la solution initiale
est donnée par la solution initiale
![]() :
:
La valeur de
![]() est obtenue à partir d'un développement limité
en temps à l'ordre 2 de la solution au premier pas en temps
est obtenue à partir d'un développement limité
en temps à l'ordre 2 de la solution au premier pas en temps
![]() :
:
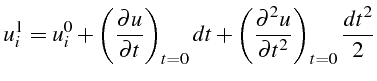
La valeur de
![]() est fournie par la seconde
condition initiale, et on utilise l'équation exacte pour calculer
est fournie par la seconde
condition initiale, et on utilise l'équation exacte pour calculer
![]() en fonction de
en fonction de
![]() ,
que l'on discrétise ensuite par différences finies centrées:
,
que l'on discrétise ensuite par différences finies centrées:
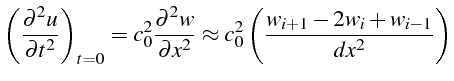
On obtiens ainsi la valeur de
![]() avec une précision
avec une précision
![]() ,
identique à celle du schéma:
,
identique à celle du schéma:
Le programme Matlab (3.5.4) implémente ce calcul pour les
2 conditions initiales étudiées: le créneau (lignes 14 à 15) et l'onde
stationnaire (lignes 18 à 19). L'initialisation des champs utilise
les relations précédentes (3.55) et (3.56) (lignes
22 à 24). Dans les itérations en temps (lignes 27 à 30), on utilise
l'équation aux différences (3.50) pour les noeuds internes
![]() en utilisant la programmation matricielle Matlab (ligne 27)
. Les conditions aux limites fournissent la valeur aux noeuds frontières
en utilisant la programmation matricielle Matlab (ligne 27)
. Les conditions aux limites fournissent la valeur aux noeuds frontières
![]() et
et
![]() (ligne 28).
(ligne 28).
% resolution equation des ondes clear; L=1; c0=2; N=201; dx=2*L/(N-1); CFL=0.8 dt=CFL*dx/c0; Tf=4*L/c0; nit=round(Tf/dt); X=[-L:dx:L]; % noeuds internes I=[2:N-1]; Ip1=[3:N]; Im1=[1:N-2]; % C.I. cas=1; if (cas==1) % C.I. cas 1 delta=0.05; W=(X<=delta).*(X>=-delta); else % C.I. cas 2 m=20; W=cos((2*m+1)*pi/2*X/L); Ue=W; end % initialisation du calcul Un0=W; Un(I)=W(I)+CFL^2/2*(W(Im1)-2*W(I)+W(Ip1)); Un(1)=0; Un(N)=0; % iteration en temps for it=2:nit Un1(I)=2*Un(I)-Un0(I)+CFL^2*(Un(Im1)-2*Un(I)+Un(Ip1)); Un1(1)=0; Un1(N)=0; Un0=Un; Un=Un1; end;
On a tracé sur la figure (3.27) la solution numérique de
la propagation d'un créneau (cas 1) pour les deux valeurs
![]() et
et
![]() du nombre de Courant
du nombre de Courant
![]() . En comparant ces solutions
avec la solution exacte sur la figure (3.23), on constate
que pour
. En comparant ces solutions
avec la solution exacte sur la figure (3.23), on constate
que pour
![]() on obtiens la solution exacte. Pour
on obtiens la solution exacte. Pour
![]() ,
des oscillations hautes fréquences apparaissent à l'arrière du créneau
pour
,
des oscillations hautes fréquences apparaissent à l'arrière du créneau
pour
![]() (i.e. avant réflexion sur la frontière). Cela confirme
la dispersion numérique des hautes fréquences par le schéma pour
(i.e. avant réflexion sur la frontière). Cela confirme
la dispersion numérique des hautes fréquences par le schéma pour
![]() .
En effet la solution initiale exacte possède un nombre infinie de
modes de Fourier. La solution initiale discrète contient donc des
grands nombres d'onde, qui se propagent numériquement avec une vitesse
plus faible que
.
En effet la solution initiale exacte possède un nombre infinie de
modes de Fourier. La solution initiale discrète contient donc des
grands nombres d'onde, qui se propagent numériquement avec une vitesse
plus faible que
![]() . Cela explique l'apparition d'oscillations
hautes fréquences à l'arrière du créneau avant la réflexion (figure
3.27a). Après la réflexion sur les frontières (figure 3.27b),
ces oscillations ont été réfléchies et ont polluées tout le domaine.
. Cela explique l'apparition d'oscillations
hautes fréquences à l'arrière du créneau avant la réflexion (figure
3.27a). Après la réflexion sur les frontières (figure 3.27b),
ces oscillations ont été réfléchies et ont polluées tout le domaine.
Sur la figure (3.28), on a tracé la solution numérique avec
![]() pour une onde stationnaire de petit nombre d'onde (
pour une onde stationnaire de petit nombre d'onde (
![]() )
comparée à la solution exacte à deux instants sur une période. On
constate que la solution numérique est très proche de la solution
exacte (les courbes coïncident), ce qui montre que la dispersion numérique
est très faible pour les ondes à base fréquence.
)
comparée à la solution exacte à deux instants sur une période. On
constate que la solution numérique est très proche de la solution
exacte (les courbes coïncident), ce qui montre que la dispersion numérique
est très faible pour les ondes à base fréquence.
Par contre, pour une onde stationnaire avec un plus grand nombre d'onde
(
![]() ), on a comparé sur la figure (3.29) la solution
numérique et la solution exacte à un instant
), on a comparé sur la figure (3.29) la solution
numérique et la solution exacte à un instant
![]() , calculée avec les
mêmes paramêtres que précédemment. On note sur cette figure le déphasage
introduit par la dispersion de la solution numérique, caractérisé
pour une onde stationnaire par une amplitude déphasée.
, calculée avec les
mêmes paramêtres que précédemment. On note sur cette figure le déphasage
introduit par la dispersion de la solution numérique, caractérisé
pour une onde stationnaire par une amplitude déphasée.