3.6 Equation de transport non linéaire

Les équations de la mécanique des fluides (équations de Navier-Stokes) font intervenir des termes d'advection non-linéaire (i.e. la vitesse de convection dépend de la solution). En plus des difficultés numériques exposées précédemment pour une équation linéaire d'advection, la résolution numérique de problèmes non-linéaires d'avection se heurte à de nouvelles difficultés:

1. la solution numérique peut devenir “non-linéairement instable”, i.e. même en respectant les conditions de stabilité du schéma linéarisé, la solution non-linéaire devient instable.
2. la solution numérique peut converger vers une solution qui n'est pas solution du problème exacte, ou qui est physiquement inacceptable (i.e. qui viole une condition d'entropie).

A titre d'exemple, considérons l'équation d'advection non linéaire de Burgers

$$\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}=0$$ (3.57)

avec une condition initiale $u(x,t=0)=u_{0}(x)$ discontinue

$$u_{0}(0)=\left\{ \begin{array}{ll} u_{l} & x\leq x_{0} u_{r} & x>x_{0}\end{array}\right.$$ (3.58)

La solution exacte est un choc qui se propage avec la célérité $s$ , et qui vérifie la relation de saut d'Hugoniot

$$F(u_{l})-F(u_{r})=s [u_{l}-u_{r}]$$ (3.59)

où $F(u)=\frac{1}{2}u^{2}$ est la fonction flux de l'équation de Burgers (3.57), qui s'écrit sous forme conservative:

$$\frac{\partial u}{\partial t}+\frac{\partial}{\partial x}(\frac{1}{2}u^{2})=0$$ (3.60)

La relation de saut (3.59) fournit la valeur de la célérité $s$

$$s=\frac{1}{2}(u_{l}+u_{r})$$

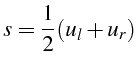
L'extension naturelle du schéma différence finie décentrée (3.29) à l'équation de Burgers (3.57) peut s'écrire:

$$\frac{u_{i}^{n+1}-u_{i}^{n}}{dt}+u_{i-1}^{n}\frac{u_{i}^{n}-u_{i-1}^{n}}{dx}=0$$ (3.61)

en utilisant une vitesse de convection décentrée $u_{i-1}^{n}$ , ou

$$\frac{u_{i}^{n+1}-u_{i}^{n}}{dt}+u_{i}^{n}\frac{u_{i}^{n}-u_{i-1}^{n}}{dx}=0$$ (3.62)

en utilisant une vitesse de convection centrée $u_{i}^{n}$ .

Figure 3.30: Solution exacte et approchées de l'équation de Burgers avec 2 schémas décentrés non conservatifs

[dx=0.01]

[dx=0.001]

Sur la figure (3.30), on a comparé la solution exacte avec la solution numérique calculée avec les 2 schémas décentrés (3.61) et (3.62) et pour deux maillages de $N=101$ et $N=1001$ points. On constate que les deux solutions numériques ne convergent pas vers la solution exacte, et donnent une célérité $s$ 20% trop petite avec le schéma upwind1 (3.61) et 20% trop grande avec le schéma upwind2 (3.62).

Pour éviter ce comportement, il faut imposer une condition supplémentaire au schéma numérique. Il faut que le schéma soit conservatif, i.e. soit écrit sous une forme conservative.

On part de l'équation exacte sous forme conservative:

$$\frac{\partial u}{\partial t}+\frac{\partial F(u)}{\partial x}=0$$ (3.63)

Un schéma conservatif par différences finies s'écrit:

$$u_{i}^{n+1}=u_{i}^{n}-\frac{dt}{dx}\left[F_{i+\frac{1}{2}}-F_{i-\frac{1}{2}}\right]$$ (3.64)

où $F_{i+\frac{1}{2}}$ est un flux numérique en $x=x_{i}+\frac{dx}{2}$ . Cette discrétisation correspond correspond à l'approximation par volume finie de (3.63) obtenue en intégrant l'équation en espace sur la cellule $[x_{i}-\frac{dx}{2},x_{i}+\frac{dx}{2}]$ et en temps entre $t^{n}$ et $t^{n+1}$ :

$$\int_{x_{i-1/2}}^{x_{i+1/2}}u(x,t^{n+1})dx = \int_{x_{i-1/2}}^{x_{i+1/2}}u(x,t^{n})dx$$

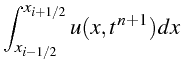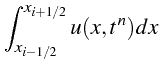$$- \left[\int_{t^{n}}^{t^{n+1}}F(u(x_{i+1/2},t)dt-\int_{t^{n}}^{t^{n+1}}F(u(x_{i-1/2},t)dt\right]$$

La valeur approchée $u_{i}^{n}$ est donc une approximation de la valeur moyenne sur la cellule:

$$u_{i}^{n}\approx\frac{1}{dx}\int_{x_{i-1/2}}^{x_{i+1/2}}u(x,t^{n})dx$$

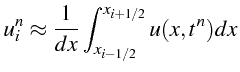
et la valeur du flux numérique $F_{i+\frac{1}{2}}$ une valeur approchée du flux physique entre $t^{n}$ et $t^{n+1}$ :

$$F_{i+\frac{1}{2}}=\frac{1}{dt}\int_{t^{n}}^{t^{n+1}}F(u(x_{i+1/2},t)dt$$

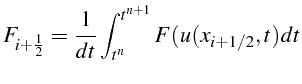
Ainsi le schéma explicite décentré conservatif pour l'équation de Burgers s'écrit:

$$u_{i}^{n+1}=u_{i}^{n}-\frac{dt}{dx}\left[\frac{1}{2}\left(u_{i}^{n}\right)^{2}-\frac{1}{2}\left(u_{i-1}^{n}\right)^{2}\right]$$ (3.65)

Figure: Solution exacte et approchée de l'équation de Burgers avec le schéma conservatif (3.65)

[dx=0.01]

[dx=0.001]

Sur la figure (3.31), on a comparé la solution exacte de l'équation de Burgers (3.57,3.58) avec la solution numérique calculée avec le schéma conservatif décentré (3.65) pour deux maillages de $N=101$ et $N=1001$ points. On constate qu'avec ce schéma conservatif, la solution approchée converge vers la solution exacte et fournit la bonne vitesse de propagation $s=\frac{u_{l}+u_{r}}{2}$ .