suivant: 3.5 Équation des ondes monter: 3. Étude de schémas précédent: 3.3 Équation de transport Table des matières
On veut déterminer la répartition de température
![]() dans un fluide
incompressible de vitesse
dans un fluide
incompressible de vitesse
![]() et de conductivité thermique
et de conductivité thermique
![]() entre 2 sections
entre 2 sections
![]() et
et
![]() où la température est maintenue
constante. L'équation de conservation de l'énergie s'écrit pour un
régime stationnaire:
où la température est maintenue
constante. L'équation de conservation de l'énergie s'écrit pour un
régime stationnaire:
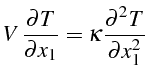
avec les conditions aux limites
![]() et
et
![]() . En
notant
. En
notant
![]() ,
,
![]() , le
problème modèle s'écrit:
, le
problème modèle s'écrit:
où
![]() est le nombre de Péclet, nombre sans
dimension caractéristique du problème.
est le nombre de Péclet, nombre sans
dimension caractéristique du problème.
La solution analytique de (3.35) est obtenue facilement avec
Maple en utilisant la fonction
![]() . Elle s'écrit:
. Elle s'écrit:
L'allure de cette solution est tracée sur la figure (3.19)
pour différentes valeurs du nombre de Péclet
![]() . Sur cette figure
on constate que se développe une couche limite thermique dont l'épaisseur
. Sur cette figure
on constate que se développe une couche limite thermique dont l'épaisseur
![]() décroît lorsque le nombre de Péclet augmente. Plus précisément,
en définissant l'épaisseur
décroît lorsque le nombre de Péclet augmente. Plus précisément,
en définissant l'épaisseur
![]() , comme étant la distance à la
paroi du point où la température relative décroit de
, comme étant la distance à la
paroi du point où la température relative décroit de
![]() % , le
rapport
% , le
rapport
![]() vérifie:
vérifie:
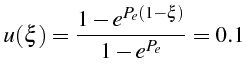
soit, en réarrangeant les termes:
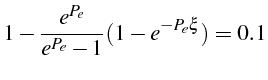
Pour des grands nombres de Péclet, cette relation conduit à :
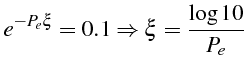
L'épaisseur de la couche limite thermique est donc inversement
proportionnelle au nombre de
![]() . Le problème devient numériquement
de plus en plus raide lorsque
. Le problème devient numériquement
de plus en plus raide lorsque
![]() augmente.
augmente.
La discrétisation par différences finies centrées de l'équation de convection diffusion (3.35) s'écrit:
Le problème étant stationnaire, on ne fait que l'analyse de la consistance du schéma (3.35). Ceci peut être fait avec Maple, et on obtiens l'erreur de troncature suivante:
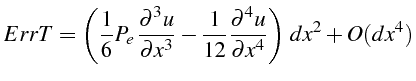
que l'on peut transformer en dérivant 2 fois l'équation (3.35):
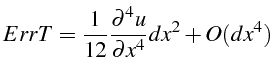
Le schéma (3.37) est donc consistant à l'équation (3.35) et d'ordre 2.
Pour poursuivre l'analyse, nous allons déterminer la solution de l'équation
aux différences (3.37) avec le programme Maple (3.4.3)
pour un maillage de
![]() points.
points.
> restart:
# Etude de l'equation de convection diffusion
> Pe*diff(U(x),x)-diff(U(x),x$2)=0;eq:=%:
> U(0)=0,U(1)=1; CL:=%:
# determination de la solution exacte
> dsolve({eq,CL},U(x)):simplify(%):
> uex:=unapply(rhs(%),x);
# Schema de D.F. centree
> Pe*(U[i+1]-U[i-1])/(2*dx)-(U[i+1]-2*U[i]+U[i-1])/dx^2=0;eqh:=%:
# Solution exacte de l'equation D.F
> eqh;
> collect(simplify(dx^2*eqh),[U[i],U[i+1],U[i-1]]);eq1:=%:
> subs(Pe=Peh/dx,eq1);eq2:=%:
# Relation de recurrence a trois niveaux:
# recherche des racines de l'equation caracteristique
> subs(U[i]=lambda,U[i-1]=1,U[i+1]=lambda^2,eq2);
> Lambda:=[solve(%,lambda)];
# Solution generale
> Ug:=unapply(C1*Lambda[1]^i+C2*Lambda[2]^i,i);
# Determination des constantes avec les C.L.
> Ug(0);Ug(N)=1;solve({%,%%},{C1,C2});rel:=%:
> Uh:=unapply(simplify(subs(rel,Ug(i))),i);
# Etude de la convergence vers la solution exacte
> subs(Pe=Peh*N,uex(i/N));Uexi:=%:
> Uh(i);
> subs(Peh=Pe*dx,i=k*N,N=1/dx,Uexi);subs(Peh=Pe*dx,i=k*N,N=1/dx,Uh(i));
> simplify(taylor(%%-%,dx,4));
# Donc convergence d'ordre 2
On commence par déterminer la solution exacte de l'équation (3.35) (lignes 6 à 7), puis on écrit le schéma aux différences finies (3.37) sous la forme d'une relation de récurrence à 3 niveaux (lignes 11 à 13):
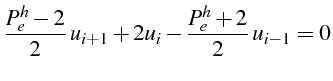
en introduisant le nombre de Péclet de maille
![]() :
:
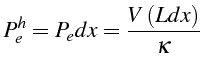
qui est un nombre de Péclet basé sur la longueur de la maille de calcul
(ici
![]() dans le domaine physique
dans le domaine physique
![]() ).
).
La solution générale de cette relation de récurrence s'écrit en fonction
des racines
![]() de l'équation caractéristique associée (calculées
aux lignes 16 et 17) sous la forme (ligne 19):
de l'équation caractéristique associée (calculées
aux lignes 16 et 17) sous la forme (ligne 19):
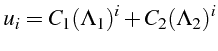
Les constantes
![]() et
et
![]() sont déterminées par les conditions
aux limites
sont déterminées par les conditions
aux limites
![]() et
et
![]() (lignes 21 et 22). D'où la solution
exacte de l'équation aux différences (3.37):
(lignes 21 et 22). D'où la solution
exacte de l'équation aux différences (3.37):
qu'il faut comparer à la solution exacte (3.36) calculée
aux noeuds du maillage
![]() , qui s'écrit en introduisant
, qui s'écrit en introduisant
![]() (lignes 24 et 25) :
(lignes 24 et 25) :
Pour étudier la convergence, on se place en un point
![]() fixé et on étudie l'écart
fixé et on étudie l'écart
![]() lorsque
lorsque
![]() tends vers zéro. Pour cela on écrit tous les paramètres (
tends vers zéro. Pour cela on écrit tous les paramètres (
![]() ,
,
![]() ,
,
![]() ) en fonction de
) en fonction de
![]() en notant que le rapport
en notant que le rapport
![]() reste constant (car le point
reste constant (car le point
![]() est fixé). On calcul ensuite un
développement en série de Taylor de l'écart en fonction de
est fixé). On calcul ensuite un
développement en série de Taylor de l'écart en fonction de
![]() (lignes
26 à 27). Le résultat donné par Maple est le suivant:
(lignes
26 à 27). Le résultat donné par Maple est le suivant:
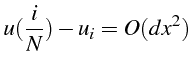
La solution numérique converge vers la solution exacte avec une précision d'ordre 2 (ce que nous donnait l'erreur de troncature).
L'expression de la solution numérique (3.37) montre que l'on
approxime des exponentielles par des fonctions puissances. De plus,
pour un maillage fixé (i.e. avec un nombre de points
![]() donné),
on constate que le terme dans les fonctions puissances
donné),
on constate que le terme dans les fonctions puissances
![]() devient négatif lorsque l'on augmente le nombre de Péclet
devient négatif lorsque l'on augmente le nombre de Péclet
![]() .
D'un point à l'autre la solution change alors de signe et oscille.
Plus précisément, pour des valeurs de
.
D'un point à l'autre la solution change alors de signe et oscille.
Plus précisément, pour des valeurs de
![]() telles que:
telles que:
la solution numérique présente des oscillations numériques (et non une instabilité numérique). Pour comprendre l'apparition de ces oscillations, considérons le maillage avec 3 points de la figure ci-dessous:
![\includegraphics[scale=0.2]{CHAP3/conv3p}](img1397.png)
Les valeurs en
![]() et en
et en
![]() sont fixées par les conditions
aux limites et le seul degré de liberté est la valeur
sont fixées par les conditions
aux limites et le seul degré de liberté est la valeur
![]() . Cette
valeur
. Cette
valeur
![]() doit être tel qu'au niveau discret, on vérifie:
doit être tel qu'au niveau discret, on vérifie:
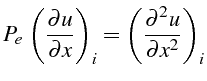
soit
Avec la discrétisation choisie, le membre de gauche est constant et
indépendant de
![]() . Le membre de droite est la valeur approchée
de la dérivée seconde au noeud 1 de la courbe passant par les 3 points
. Le membre de droite est la valeur approchée
de la dérivée seconde au noeud 1 de la courbe passant par les 3 points
![]() . La valeur de
. La valeur de
![]() est donc telle que la
courbure est égale à la valeur du membre de gauche. Cette valeur augmentant
avec le nombre de Péclet, la courbure augmente et la valeur de
est donc telle que la
courbure est égale à la valeur du membre de gauche. Cette valeur augmentant
avec le nombre de Péclet, la courbure augmente et la valeur de
![]() s'éloigne par valeur négative de la valeur moyenne
s'éloigne par valeur négative de la valeur moyenne
![]() (qui correspond à une courbure nulle). D'après (3.41), la
valeur de
(qui correspond à une courbure nulle). D'après (3.41), la
valeur de
![]() s'écrit:
s'écrit:
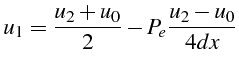
Cette valeur de
![]() devient inférieur à
devient inférieur à
![]() dès que
dès que
![]() ,
qui est justement la condition (3.40) d'apparition des oscillations
numériques.
,
qui est justement la condition (3.40) d'apparition des oscillations
numériques.
Ces oscillations numériques apparaissent dans la couche limite thermique en présence de forte courbure. Elles indiquent que le maillage est insuffisant pour décrire précisément la courbure de la couche limite.
% resolution de l'equation de convection diffusion %clear; % parametres N=11; Peh=2.1 L=1.0; dx=1/(N-1); Pe=Peh/dx; X=[0:dx:L]; % definition du schema D.F. operateur a=[-(Peh+2)/2 2 (Peh-2)/2] % construction des matrices tridiag e=ones(1,N); A=[a(1)*e; a(2)*e; a(3)*e]; B=zeros(1,N); % C.L dirichlet en 1 et N A(:,1)=0; A(2,1)=1; B(1)=0; A(:,N)=0; A(2,N)=1; B(N)=1; % resolution U=tridiag(A,B); % trace solution finale clf; figure(1); Xe=[0:1/100:L]; Ue=(exp(Pe*Xe)-1)/(exp(Pe)-1); plot(X,U,Xe,Ue);
Nous avons programmé le schéma centré avec Matlab (programme 3.4.4).
Sur la figure (3.20), on a comparée la solution numérique
calculée avec
![]() points et la solution exacte pour différentes
valeurs de
points et la solution exacte pour différentes
valeurs de
![]() . On constate que pour
. On constate que pour
![]() , la
solution numérique est proche de la solution exacte et ne présente
aucune oscillation. Par contre pour
, la
solution numérique est proche de la solution exacte et ne présente
aucune oscillation. Par contre pour
![]() , la solution numérique
présente des oscillations, qui montre que le maillage n'est plus assez
fin pour capter la solution exacte.
, la solution numérique
présente des oscillations, qui montre que le maillage n'est plus assez
fin pour capter la solution exacte.
[cas ![\includegraphics[width=0.3\paperwidth,keepaspectratio]{CHAP3/convdif1}](img1408.png) [cas [cas ![\includegraphics[width=0.3\paperwidth,keepaspectratio]{CHAP3/convdif2}](img1409.png)
|
Pour éviter les oscillations numériques, on peut utiliser une discrétisation
décentrée du terme de convection, comme au paragraphe (3.3.7).
On obtiens ainsi un schéma décentré (ou upwind), qui s'écrit pour
![]() :
:
L'analyse de l'erreur de troncature s'effectue avec Maple comme pour le schéma centré, et on obtiens l'erreur de troncature suivante:
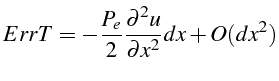
Le schéma décentré (3.42) est donc bien consistant à l'équation (3.35) et d'ordre 1. Cette erreur de troncature montre aussi que ce schéma décentré 3.42 est équivalent à l'équation de convection diffusion suivante:
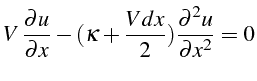
Le schéma décentré introduit donc une diffusion numérique supplémentaire
![]() par rapport à la diffusion physique
par rapport à la diffusion physique
![]() . Ce
schéma décentré est donc sur-dissipatif. En suivant la même démarche
qu'au paragraphe 3.4.3, on peut déterminer la solution analytique
de l'équation aux différences (3.42). Pour cela on écrit
le schéma aux différences finies (3.42) sous la forme d'une
relation de récurrence à 3 niveaux:
. Ce
schéma décentré est donc sur-dissipatif. En suivant la même démarche
qu'au paragraphe 3.4.3, on peut déterminer la solution analytique
de l'équation aux différences (3.42). Pour cela on écrit
le schéma aux différences finies (3.42) sous la forme d'une
relation de récurrence à 3 niveaux:
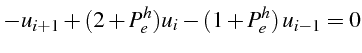
La solution générale de cette relation de récurrence s'écrit en fonction
des racines
![]() de l'équation caractéristique
associée sous la forme:
de l'équation caractéristique
associée sous la forme:
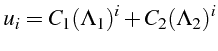
Les constantes
![]() et
et
![]() sont déterminées par les conditions
aux limites
sont déterminées par les conditions
aux limites
![]() et
et
![]() . La solution exacte de l'équation
aux différences (3.42) s'écrit:
. La solution exacte de l'équation
aux différences (3.42) s'écrit:
Cette solution numérique converge vers la solution exacte aux noeuds
du maillage (3.39), mais uniquement à l'ordre 1 (comme prévu
par l'erreur de troncature). Un développement limité de l'écart
![]() montre que cet écart est d'ordre 1:
montre que cet écart est d'ordre 1:
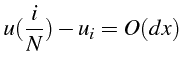
contrairement à la solution numérique du schéma centré (3.38)
qui converge à l'ordre 2. Si on compare maintenant cette solution
numérique
![]() à la solution exacte
à la solution exacte
![]() de l'équation équivalente
(3.43) fournie par l'analyse de troncature:
de l'équation équivalente
(3.43) fournie par l'analyse de troncature:
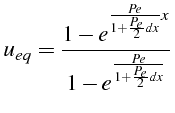
on montre que l'écart
![]() est alors d'ordre
2:
est alors d'ordre
2:
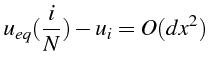
Le nombre de Péclet effectif de la solution numérique est donc plus
petit que le nombre de Péclet exacte et vaut
![]() .
Le schéma décentré a donc introduit de la diffusion numérique.
Grâce à cette diffusion numérique, la solution
.
Le schéma décentré a donc introduit de la diffusion numérique.
Grâce à cette diffusion numérique, la solution
![]() reste toujours
comprise entre les deux valeurs des conditions limites (0 et 1), sans
oscillations.
reste toujours
comprise entre les deux valeurs des conditions limites (0 et 1), sans
oscillations.
% resolution de l'equation de convection diffusion %clear; % parametres N=11; Peh=1/2 L=1.0; dx=1/(N-1); Pe=Peh/dx; X=[0:dx:L]; % definition du schema D.F. operateur a=[-(Peh+1) 2+Peh -1] % construction des matrices tridiag e=ones(1,N); A=[a(1)*e; a(2)*e; a(3)*e]; B=zeros(1,N); % C.L dirichlet en 1 et N A(:,1)=0; A(2,1)=1; B(1)=0; A(:,N)=0; A(2,N)=1; B(N)=1; % resolution U=tridiag(A,B); % trace solution finale clf; figure(1); Xe=[0:1/100:L]; Ue=(exp(Pe*Xe)-1)/(exp(Pe)-1); plot(X,U,Xe,Ue);
Nous avons programmé le schéma décentré avec Matlab (programme 3.4.6).
Sur la figure 3.21, on a comparée la solution numérique
calculée avec
![]() points et la solution exacte pour différentes
valeurs de
points et la solution exacte pour différentes
valeurs de
![]() .
.
En comparant avec la solution numérique obtenue avec le schéma centré
(figure 3.20), on constate que pour
![]() , la
solution décentrée est moins précise que la solution centrée. Par
contre pour
, la
solution décentrée est moins précise que la solution centrée. Par
contre pour
![]() , la solution décentrée reste monotone,
mais en restant assez loin de la solution exacte.
, la solution décentrée reste monotone,
mais en restant assez loin de la solution exacte.
[![\includegraphics[width=0.3\paperwidth,keepaspectratio]{CHAP3/convdifup1}](img1425.png) [ [![\includegraphics[width=0.3\paperwidth,keepaspectratio]{CHAP3/convdifup2}](img1426.png)
|
Enfin sur la figure (3.22), on a comparé la solution numérique
(
![]()
![]() ) à la solution exacte calculée avec le nombre
de Péclet
) à la solution exacte calculée avec le nombre
de Péclet
![]() et le nombre de Péclet équivalent
et le nombre de Péclet équivalent
![]() . On
constate que la solution numérique décentrée est beaucoup plus proche
de la solution avec le nombre de Péclet éffectif
. On
constate que la solution numérique décentrée est beaucoup plus proche
de la solution avec le nombre de Péclet éffectif
![]() , qu'avec
le nombre de Péclet exacte
, qu'avec
le nombre de Péclet exacte
![]() , ce qui confirme l'analyse précédente.
, ce qui confirme l'analyse précédente.
![\includegraphics[width=0.3\paperwidth,keepaspectratio]{CHAP3/convdifup3}](img1430.png)
|