suivant: 5.4 Écoulements réels monter: 5. Modélisation numérique des précédent: 5.2 Tube à choc Table des matières
Avant d'étudier les méthodes numériques pour les équations d'Euler, nous ferons quelques rappels sur la simulation numérique de problème d'advection linéaire.
Considérons l'équation d'advection linéaire suivante:
Pour calculer une solution approchée ![]() de la solution exacte
de la solution exacte
![]() , on introduit un maillage en espace de pas
, on introduit un maillage en espace de pas ![]() et une
discrétisation en temps de pas
et une
discrétisation en temps de pas ![]() . Classiquement, on calcule la
solution approchée
. Classiquement, on calcule la
solution approchée ![]() par discrétisation différences finies
de l'équation exacte. La solution approchée
par discrétisation différences finies
de l'équation exacte. La solution approchée ![]() est alors
interprétée comme l'approximation de la solution exacte au point de
maillage
est alors
interprétée comme l'approximation de la solution exacte au point de
maillage ![]() ,
, ![]() :
:
On peut cependant donner une autre interprétation de ![]() (dans un cadre volumes finis). La solution approchée est une approximation
de la valeur moyenne de la solution exacte dans la cellule entourant
le noeud
(dans un cadre volumes finis). La solution approchée est une approximation
de la valeur moyenne de la solution exacte dans la cellule entourant
le noeud ![]() :
:
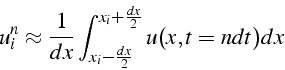
C'est cette interprétation que nous utiliserons lors de l'application des schémas à des équations de bilan (équation d'Euler), puisqu'elle va permettre de caractériser les propriétés de conservation du schéma numérique.
Pour étudier la convergence de la solution numérique ![]() du schéma aux différences finies vers la solution exacte
du schéma aux différences finies vers la solution exacte ![]() de l'équation, on utilise un résultat d'analyse du à Lax (Richtmyer
et Norton 1967):
de l'équation, on utilise un résultat d'analyse du à Lax (Richtmyer
et Norton 1967):
Le schéma le plus simple est le schéma explicite centré, qui utilise une discrétisation centrée de la dérivée spatiale. Il s'écrit:
C'est un schéma explicite qui calcule la valeur inconnue ![]() à l'étape
à l'étape ![]() en fonction des valeurs connues
en fonction des valeurs connues
![]() à l'étape
à l'étape ![]() .
.
Pour étudier la stabilité, on calcule le facteur d'amplification ![]() du schéma. En introduisant le paramètre sans dimension
du schéma. En introduisant le paramètre sans dimension ![]() ou
nombre de Courant Fredrich Lewis, dit aussi nombre de Courant:
ou
nombre de Courant Fredrich Lewis, dit aussi nombre de Courant:
le carré du module du facteur d'amplification ![]() du schéma vérifie:
du schéma vérifie:
Le module de ![]() est donc toujours plus grand que 1 et le schéma
est inconditionnellement instable.
est donc toujours plus grand que 1 et le schéma
est inconditionnellement instable.
Le schéma centré explicite (5.8) est donc inutilisable pour résoudre l'équation de convection pure (5.7).
Pour comprendre la raison de cette instabilité, nous allons faire l'étude de la consistance de ce schéma. L'erreur de troncature du schéma est la suivante:
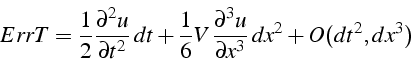
Le schéma est donc bien consistant à l'équation (5.7), mais instable. Pour comprendre cette instabilité, étudions le premier terme de l'erreur:
En dérivant l'équation (5.7) par rapport au temps, nous
pouvons en déduire (en utilisant à nouveau l'équation (5.7))
que la solution ![]() vérifie:
vérifie:
d'où l'expression du premier terme (5.10) de l'erreur de troncature:
Par définition de l'erreur de troncature, qui est l'écart entre l'équation
approchée ![]() et l'équation exacte
et l'équation exacte ![]() , calculée pour la solution
exacte
, calculée pour la solution
exacte ![]() , on a donc:
, on a donc:
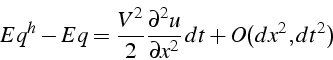
Avec ce schéma explicite centré, on ne résout donc pas l'équation
exacte, mais l'équation équivalente suivante (en notant
![]() ):
):
C'est une équation de convection-diffusion classique, mais avec un
coefficient de diffusion négatif ![]() , qui au lieu de diffuser
l'énergie de la solution, apporte indéfiniment de l'énergie au système.
En effet, en décomposant la solution initiale en série de Fourier:
, qui au lieu de diffuser
l'énergie de la solution, apporte indéfiniment de l'énergie au système.
En effet, en décomposant la solution initiale en série de Fourier:
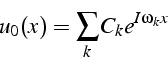
on vérifie que la solution de l'équation (5.13) s'écrit:
Pour ![]() , on retrouve la solution générale de l'équation de
convection pure (5.7), qui est convectée sans déformation.
Si
, on retrouve la solution générale de l'équation de
convection pure (5.7), qui est convectée sans déformation.
Si ![]() , la solution est convectée mais décroıt exponentiellement
(problème de convection diffusion classique). Par contre si
, la solution est convectée mais décroıt exponentiellement
(problème de convection diffusion classique). Par contre si ![]() la solution est convectée mais croit exponentiellement. Ce dernier
cas correspond à la solution numérique du schéma explicite centré
(5.8), qui croıt exponentiellement et est instable.
la solution est convectée mais croit exponentiellement. Ce dernier
cas correspond à la solution numérique du schéma explicite centré
(5.8), qui croıt exponentiellement et est instable.
Le schéma explicite (5.8) étant instable parce qu'insuffisamment diffusif, on peut le rendre stable en ajoutant un terme de diffusion numérique qui va compenser le premier terme de l'erreur de troncature (5.12), responsable de l'instabilité. Pour cela, il suffit de retrancher à l'équation (5.8) la discrétisation du premier terme de l'erreur de troncature (5.12):
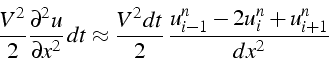
Le schéma ainsi obtenu s'écrit:
C'est un schéma de Lax-Wendroff. Ce schéma est à la base de nombreux schémas utilisés en mécanique des fluides pour traiter les problèmes à convection dominante.
C'est un schéma explicite qui calcule la valeur inconnue ![]() à l'étape
à l'étape ![]() en fonction des valeurs connues
en fonction des valeurs connues
![]() à l'étape
à l'étape ![]()
L'analyse de stabilité fournit le carré du module du facteur d'amplification
![]() du schéma, en posant
du schéma, en posant ![]() :
:
C'est un polynôme de degré 2 en ![]() , que l'on étudie pour
, que l'on étudie pour ![]() .
En
.
En ![]() , ce polynôme vaut
, ce polynôme vaut ![]() et sa dérivée s'annule. La condition
de stabilité
et sa dérivée s'annule. La condition
de stabilité
![]() impose
donc que sa valeur en
impose
donc que sa valeur en ![]() soit plus petite que
soit plus petite que ![]() :
:
ce qui impose la condition de stabilité classique sur le nombre de Courant:
L'erreur de troncature, qui s'écrit, en tenant compte de la propriété (5.11) :
Le schéma de Lax-Wendroff (5.15) est donc consistant
à l'équation de convection pure (5.7), d'ordre
![]() et conditionnellement stable, avec une condition de stabilité donnée
par (5.16).
et conditionnellement stable, avec une condition de stabilité donnée
par (5.16).
On le vérifie numériquement en calculant la convection d'une tache gaussienne
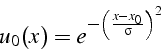
convectée par un champ de vitesse constant ![]() . La solution exacte
est
. La solution exacte
est
![]() .
.
Sur la figure (5.2a), on a tracé la solution numérique
pour différents ![]() à
à ![]() . On constate la très bonne coıncidence
entre la solution numérique et la solution exacte pour tous les
. On constate la très bonne coıncidence
entre la solution numérique et la solution exacte pour tous les ![]() .
Pour faire une analyse plus fine, on a tracé sur la figure (5.2b)
l'erreur entre la solution exacte et la solution numérique. On constate
que l'erreur est très faible (
.
Pour faire une analyse plus fine, on a tracé sur la figure (5.2b)
l'erreur entre la solution exacte et la solution numérique. On constate
que l'erreur est très faible (![]() %). Cette erreur croıt lorsque
le
%). Cette erreur croıt lorsque
le ![]() décroıt pour atteindre une limite (obtenue dès
décroıt pour atteindre une limite (obtenue dès ![]() puisque les courbes pour
puisque les courbes pour ![]() et
et ![]() sont indiscernables).
Cette erreur est liée à l'erreur de discrétisation spatiale, et décroıt
lorsque l'on augmente
sont indiscernables).
Cette erreur est liée à l'erreur de discrétisation spatiale, et décroıt
lorsque l'on augmente ![]() .
.
[solution numérique]![\includegraphics[width=0.3\paperwidth,keepaspectratio]{CHAP5/convexp1}](img866.png) [erreur à [erreur à ![\includegraphics[width=0.3\paperwidth,keepaspectratio]{CHAP5/convexp2}](img867.png)
|
Pour ![]() , l'erreur est nulle, et on obtient dans ce cas la
solution exacte. En effet l'équation (5.15) conduit pour
, l'erreur est nulle, et on obtient dans ce cas la
solution exacte. En effet l'équation (5.15) conduit pour
![]() à:
à:
qui est la solution exacte car les deux points ![]() et
et ![]() se trouvent sur la même trajectoire, puisque:
se trouvent sur la même trajectoire, puisque:
Une autre façon de stabiliser le schéma explicite (5.8),
est d'utiliser une discrétisation décentrée du terme convectif
![]() .
Ce terme représente la convection de
.
Ce terme représente la convection de ![]() par le champ de vitesse
par le champ de vitesse
![]() , et si
, et si ![]() la convection transporte du scalaire
la convection transporte du scalaire ![]() de la
gauche vers la droite (et inversement si
de la
gauche vers la droite (et inversement si ![]() ). D'où l'idée d'utiliser
une discrétisation décentrée de ce terme qui, si
). D'où l'idée d'utiliser
une discrétisation décentrée de ce terme qui, si ![]() , fait intervenir
les valeurs de
, fait intervenir
les valeurs de ![]() aux noeuds amonts
aux noeuds amonts ![]() et
et ![]() :
:
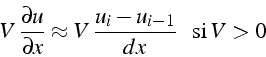
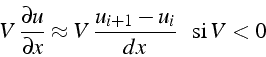
Le schéma ainsi obtenu s'écrit pour ![]() :
:
C'est un schéma explicite qui donne la valeur inconnue ![]() à l'étape
à l'étape ![]() en fonction des valeurs connues
en fonction des valeurs connues
![]() à l'étape
à l'étape ![]() . On note que la valeur aval
. On note que la valeur aval ![]() n'intervient
pas dans ce cas pour le calcul de
n'intervient
pas dans ce cas pour le calcul de ![]() .
.
L'analyse de stabilité fournit le carré du module du facteur d'amplification
![]() du schéma, qui s'écrit:
du schéma, qui s'écrit:
C'est une fonction affine de ![]() que l'on étudie pour
que l'on étudie pour ![]() ,
qui vaut 1 en
,
qui vaut 1 en ![]() . La condition de stabilité
. La condition de stabilité
![]() impose donc que sa valeur en
impose donc que sa valeur en ![]() soit plus petite que
soit plus petite que ![]() :
:
ce qui conduit à la condition de stabilité classique:
L'erreur de troncature s'écrit:
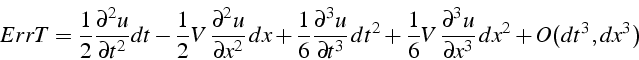
soit en tenant compte de la propriété (5.11) :
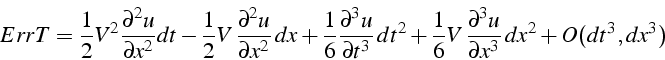
Le terme d'ordre 1 de l'erreur de troncature est donc un terme de diffusion:
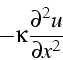
Le schéma explicite décentré est donc équivalent à l'équation de convection diffusion:
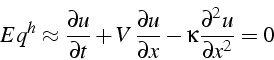
avec un coefficient de diffusion numérique ![]() :
:
Le schéma explicite décentré est donc consistant à l'équation
de convection pure et d'ordre ![]() . Il est conditionnellement
stable avec une condition de stabilité (5.19).
. Il est conditionnellement
stable avec une condition de stabilité (5.19).
Mais c'est un schéma diffusif. La solution numérique est convectée,
mais décroıt exponentiellement proportionnellement à un coefficient
de “diffusion numérique” ![]() (5.20)
si la condition de stabilité (5.19) est vérifiée. Si la
condition de stabilité (5.19) n'est pas vérifiée, la solution
numérique croıt exponentiellement puisque ce coefficient
(5.20)
si la condition de stabilité (5.19) est vérifiée. Si la
condition de stabilité (5.19) n'est pas vérifiée, la solution
numérique croıt exponentiellement puisque ce coefficient ![]() devient négatif, ce qui explique pourquoi le schéma devient instable.
devient négatif, ce qui explique pourquoi le schéma devient instable.
On le vérifie numériquement sur le problème de la convection de la gaussienne.
Sur la figure (5.3), on a tracé la solution numérique pour
différents ![]() à
à ![]() . On constate l'importante diffusion
numérique de la solution, qui augmente lorsque le
. On constate l'importante diffusion
numérique de la solution, qui augmente lorsque le ![]() diminue
pour atteindre une limite (correspondant à un coefficient de diffusion
numérique
diminue
pour atteindre une limite (correspondant à un coefficient de diffusion
numérique
![]() ). On note aussi le cas particulier
). On note aussi le cas particulier
![]() , où la solution numérique coıncide avec la solution exacte,
puisque dans ce cas particulier le coefficient de diffusion numérique
, où la solution numérique coıncide avec la solution exacte,
puisque dans ce cas particulier le coefficient de diffusion numérique
![]() est nul.
est nul.
Nous avons vu dans les paragraphes précédents que la faible diffusion
numérique d'un schéma permet d'assurer que la solution numérique est
convectée sans être trop amortie. Pour les équations hyperboliques
(équation de convection pure), il faut aussi que la solution numérique
soit convectée à la bonne vitesse avec très peu de déphasage par rapport
à la solution exacte. Pour étudier cette dispersion numérique, nous
allons considérer le cas de la convection d'une onde
![]() .
La solution exacte de l'équation de convection pure (5.7)
s'écrit:
.
La solution exacte de l'équation de convection pure (5.7)
s'écrit:
On note que cette solution initiale correspond justement à la perturbation
![]() dans la méthode de stabilité de Neumann. L'étude
de stabilité fournit le coefficient d'amplification
dans la méthode de stabilité de Neumann. L'étude
de stabilité fournit le coefficient d'amplification ![]() du schéma,
qui permet de calculer
du schéma,
qui permet de calculer
![]() en fonction de la perturbation
initiale
en fonction de la perturbation
initiale
![]() :
:
La solution numérique ![]() pour la convection d'une onde peut
donc s'écrire en fonction de la solution initiale
pour la convection d'une onde peut
donc s'écrire en fonction de la solution initiale ![]() au noeud
au noeud
![]() du maillage:
du maillage:
Le facteur d'amplification ![]() est un nombre complexe d'amplitude
est un nombre complexe d'amplitude
![]() et de phase
et de phase ![]() :
:
et la solution numérique ![]() s'écrit sous la forme:
s'écrit sous la forme:
En comparant cette expression à la solution exacte au noeud ![]() :
:
on note que ![]() , qui est le module de
, qui est le module de ![]() , nous donne l'amortissement
de l'onde et la différence
, nous donne l'amortissement
de l'onde et la différence
![]() sa dispersion.
En notant que
sa dispersion.
En notant que ![]() dépend de
dépend de ![]() , on pose
, on pose ![]() et on a
et on a
![]() . La dispersion
. La dispersion ![]() est la fonction
de
est la fonction
de ![]() suivante:
suivante:
Pour un maillage de ![]() points, les modes possibles de la solution
numérique correspondent à des pulsations
points, les modes possibles de la solution
numérique correspondent à des pulsations
![]() (
(![]() de 1 à
de 1 à ![]() ) et donc
) et donc ![]() varie de
varie de ![]() à
à
![]() .
On trouve pour le schéma décentré et le schéma explicite d'ordre 2,
en utilisant Maple pour le calcul de
.
On trouve pour le schéma décentré et le schéma explicite d'ordre 2,
en utilisant Maple pour le calcul de ![]() :
:
On a tracé sur la figure (5.4) les courbes de
On constate sur cette figure que le schéma décentré est moins dispersif que le schéma d'ordre 2. Pour valider cette analyse, nous avons effectuer la simulation numérique de la convection d'une onde.
Le champ initial est une onde
![]() (lignes 10 à
11). Les schémas étudiés sont des schémas explicites du type:
(lignes 10 à
11). Les schémas étudiés sont des schémas explicites du type:
Le schéma numérique étant explicite, la solution s'obtient simplement à chaque itération par multiplication matricielle:
Pour ce calcul, il faut introduire des conditions aux limites. La
longueur ![]() du domaine est un multiple de la longueur d'onde
de l'onde initiale
du domaine est un multiple de la longueur d'onde
de l'onde initiale
![]() . La solution vérifie donc des
conditions de périodicité en
. La solution vérifie donc des
conditions de périodicité en ![]() et
et ![]() :
:
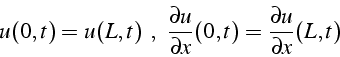
Pour le noeud ![]() , le schéma aux différences (5.23)
fait intervenir la valeur
, le schéma aux différences (5.23)
fait intervenir la valeur ![]() , que l'on calcule avec la
condition de périodicité :
, que l'on calcule avec la
condition de périodicité :
![]() . Pour le noeud
. Pour le noeud
![]() , on impose la condition
, on impose la condition
![]() .
.
On a tracé sur la figure (5.5) la solution obtenue avec le schéma décentré d'ordre 1 (5.18) et le schéma d'ordre 2 (5.15). On constate bien la dispersion du schéma d'ordre 2 (décalage des courbes), mais aussi la très forte diffusion du schéma décentré (mais qui a une dispersion plus faible).
[schèma d'ordre 1]![\includegraphics[width=0.3\paperwidth]{CHAP5/convdisp2}](img932.png) [schèma d'ordre 2] [schèma d'ordre 2]![\includegraphics[width=0.3\paperwidth,keepaspectratio]{CHAP5/convdisp1}](img933.png)
|
Pour interprèter l'apparition de cette dispersion dans le schéma d'ordre
2 (5.15), on transforme l'erreur de troncature (5.17)
en dérivant l'équation exacte pour remplacer
![]() :
:
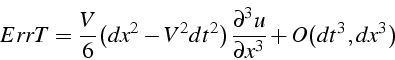
L'équation aux différences pour le schéma explicite d'ordre 2 est donc équivalente à l'équation de convection dispersion suivante:
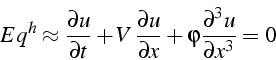
avec
![]() . La solution exacte,
pour une condition initiale
. La solution exacte,
pour une condition initiale
![]() , s'écrit:
, s'écrit:
L'onde initiale est donc transportée avec une vitesse de convection
![]() , qui dépend de la fréquence de l'onde. Les
ondes sont donc dispersées (i.e. ne se propagent pas toutes à la même
vitesse comme dans l'équation exacte (5.7)), avec une dispersion
d'autant plus grande que l'onde est à haute fréquence. On note aussi
que, pour le cas particulier
, qui dépend de la fréquence de l'onde. Les
ondes sont donc dispersées (i.e. ne se propagent pas toutes à la même
vitesse comme dans l'équation exacte (5.7)), avec une dispersion
d'autant plus grande que l'onde est à haute fréquence. On note aussi
que, pour le cas particulier ![]() , le schéma (5.15)
n'est plus dispersif, ce que l'on vérifie bien numériquement.
, le schéma (5.15)
n'est plus dispersif, ce que l'on vérifie bien numériquement.
La capture des chocs nécessite des schémas numériques qui propagent correctement les discontinuités. Nous allons donc étudier numériquement le problème d'advection suivant:
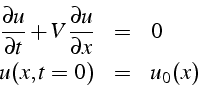
où la condition initiale ![]() est discontinue en
est discontinue en ![]()
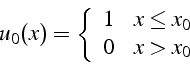
dont la solution exacte est
Sur la figure (5.6), nous avons comparé la solution exacte
avec la solution approchée calculée sur un maillage de ![]() points
(
points
(![]() ).
).
On constate que la solution numérique avec le schéma décentré d'ordre
1 (upwind) présente une forte diffusion, et la discontinuité se trouve
étalée sur une vingtaine de mailles. Avec le schéma d'ordre 2 de Lax
Wendroff, la discontinuité est mieux captée (i.e. l'étalement du front
est inférieure à 10 mailles). Si on raffine le maillage, les mêmes
conclusions peuvent être tirées, comme le montre la figure (5.7)
où on a tracé la solution numérique sur un maillage 10 fois plus fin
![]() .
.
La convergence de la solution numérique est dégradée au voisinage
de la discontinuité. La méthode décentrée d'ordre 1 converge en ![]() au lieu de
au lieu de ![]() et la méthode d'ordre 2 converge en
et la méthode d'ordre 2 converge en ![]() au lieu de
au lieu de ![]() .
.
Le comportement de la solution décentrée s'explique par la forte dissipation numérique du schéma upwind. Celui de la solution d'ordre 2 est lié à la dispersion numérique du schéma de Lax Wendroff, qui ralentit les ondes hautes fréquences. Or la convection d'une discontinuité correspond à la convection d'une infinité d'ondes basses et hautes fréquences (décomposition en série de Fourier), qui se propagent toutes à la même vitesse. Le schéma Lax Wendroff ralentit les ondes hautes fréquences, et donc la discontinuité n'est plus reconstituée exactement, et une oscillation haute fréquence apparaıt à l'arrière de la discontinuité comme le montrent les figures (5.6) et (5.7) (la fréquence de l'oscillation augmente avec le nombre de points du maillage).
En plus des difficultés numériques exposées précédemment pour une équation linéaire d'advection, la résolution numérique de problème non-linéaire se heurte à de nouvelles difficultés:
avec une condition initiale
![]() discontinue
discontinue
La solution exacte est un choc qui se propage avec la célérité ![]() ,
et qui vérifie la relation de saut d'Hugoniot
,
et qui vérifie la relation de saut d'Hugoniot
La relation de saut (5.26) fournit la valeur de la célérité
![]()
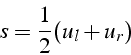
L'extension naturelle du schéma aux différences finies décentrées (5.18) à l'équation de Burgers (5.24) peut s'écrire:
en utilisant une vitesse de convection décentrée ![]() , ou
, ou
en utilisant une vitesse de convection centrée ![]() .
.
[dx=0.01]![\includegraphics[width=0.5\textwidth]{CHAP5/burgers1}](img965.png) [dx=0.001] [dx=0.001]![\includegraphics[width=0.5\textwidth]{CHAP5/burgers2}](img966.png)
|
Sur la figure (5.8), on a comparé la solution exacte avec
la solution numérique calculée avec les 2 schémas décentrés (5.28)
et (5.29) et pour deux maillages de ![]() et
et ![]() points. On constate que les deux solutions numériques ne convergent
pas vers la solution exacte, et donnent une célérité
points. On constate que les deux solutions numériques ne convergent
pas vers la solution exacte, et donnent une célérité ![]() 20% trop
petite avec le schéma upwind1 (5.28) et 20% trop grande
avec le schéma upwind2 (5.29).
20% trop
petite avec le schéma upwind1 (5.28) et 20% trop grande
avec le schéma upwind2 (5.29).
Pour éviter ce comportement, il faut imposer une condition supplémentaire au schéma numérique. Il faut que le schéma soit conservatif, i.e. soit écrit sous une forme conservative.
On part de l'équation exacte sous forme conservative:
Un schéma conservatif par différences finies s'écrit:
où
![]() est un flux numérique en
est un flux numérique en
![]() .
Cette discrétisation correspond à l'approximation par volumes finis
de (5.30) obtenue en intégrant l'équation en espace sur
la cellule
.
Cette discrétisation correspond à l'approximation par volumes finis
de (5.30) obtenue en intégrant l'équation en espace sur
la cellule
![]() et en temps
entre
et en temps
entre ![]() et
et ![]() :
:
![\begin{eqnarray*}
\int_{x_{i-1/2}}^{x_{i+1/2}}u(x,t^{n+1})dx & = & \int_{x_{i-1/...
...(x_{i+1/2},t))dt-\int_{t^{n}}^{t^{n+1}}F(u(x_{i-1/2},t))dt\right]\end{eqnarray*}](img974.png)
La valeur approchée ![]() est donc une approximation de la
valeur moyenne sur la cellule:
est donc une approximation de la
valeur moyenne sur la cellule:
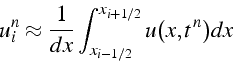
et la valeur du flux numérique
![]() une valeur approchée
du flux physique entre
une valeur approchée
du flux physique entre ![]() et
et ![]() :
:
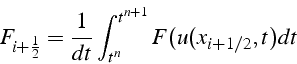
Ainsi le schéma explicite décentré conservatif pour l'équation de Burgers s'écrit:
[dx=0.01]![\includegraphics[width=0.5\textwidth]{CHAP5/burgers3}](img978.png) [dx=0.001] [dx=0.001]![\includegraphics[width=0.5\textwidth]{CHAP5/burgers4}](img979.png)
|
Sur la figure (5.9), on a comparé la solution exacte de
l'équation de Burgers (5.24,5.25) avec la solution
numérique calculée avec le schéma conservatif décentré (5.32)
pour deux maillages de ![]() et
et ![]() points. On constate qu'avec
ce schéma conservatif, la solution approchée converge vers la solution
exacte et fournit la bonne vitesse de propagation
points. On constate qu'avec
ce schéma conservatif, la solution approchée converge vers la solution
exacte et fournit la bonne vitesse de propagation
![]() .
.
Soit le système de ![]() équations hyperboliques écrit sous forme conservative:
équations hyperboliques écrit sous forme conservative:
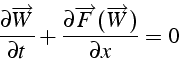
En notant
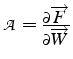 ,
la matrice jacobienne des flux, ce système s'écrit sous la forme non
conservative:
,
la matrice jacobienne des flux, ce système s'écrit sous la forme non
conservative:
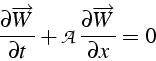
En diagonalisant la matrice ![]() , on obtient un système
de n équations d'advection dont les vitesses d'advection sont les
valeurs propres
, on obtient un système
de n équations d'advection dont les vitesses d'advection sont les
valeurs propres ![]() de
de ![]() . Pour construire
un schéma numérique décentré, il faut donc tenir compte du signe des
valeurs propres de
. Pour construire
un schéma numérique décentré, il faut donc tenir compte du signe des
valeurs propres de ![]() lors du calcul des flux à l'interface.
lors du calcul des flux à l'interface.
Considérons tout d'abord le cas linéaire (i.e. ![]() est
indépendant de
est
indépendant de ![]() ). En notant
). En notant ![]() la matrice diagonale des
valeurs propres
la matrice diagonale des
valeurs propres ![]() , la diagonalisation de
, la diagonalisation de ![]() s'écrit:
s'écrit:
Soit
![]() la matrice diagonale des valeurs
propres positives de
la matrice diagonale des valeurs
propres positives de ![]() et
et
![]() la matrice diagonale des valeurs propres négatives. On note
la matrice diagonale des valeurs propres négatives. On note
qui sont deux matrices vérifiant:
Pour calculer le flux
![]() à l'interface
à l'interface ![]() ,
on peut utiliser un flux numérique centré:
,
on peut utiliser un flux numérique centré:
![\begin{displaymath}
F_{i+1/2}^{c}=\frac{1}{2}\left[F(W_{i})+F(W_{i+1})\right]=\frac{1}{2}\mathcal{A}(W_{i}+W_{i+1})\end{displaymath}](img989.png)
Le schéma conservatif explicite décentré s'écrit alors:
En utilisant les propriétés (5.33) de ![]() , le
flux décentré s'écrit aussi sous la forme:
, le
flux décentré s'écrit aussi sous la forme:
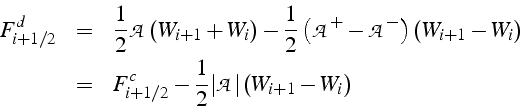
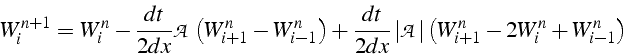
ce qui correspond à un schéma centré avec un terme supplémentaire de dissipation qui stabilise le schéma centré.
La condition de stabilité de ce schéma est une condition de type ![]() basée sur les vitesses d'advection du système, i.e. sur les valeurs
propres de
basée sur les vitesses d'advection du système, i.e. sur les valeurs
propres de ![]() :
:
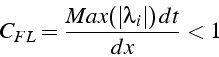
Pour un problème non-linéaire, la matrice ![]() dépend de
la solution
dépend de
la solution ![]() . L'analyse précédente doit être modifiée. Pour cela
on considère un état intermédiaire
. L'analyse précédente doit être modifiée. Pour cela
on considère un état intermédiaire ![]() pour calculer la
valeur
pour calculer la
valeur
![]() de
de ![]() intervenant dans
le calcul du flux décentré (5.34). Pour obtenir un schéma
conservatif, la matrice
intervenant dans
le calcul du flux décentré (5.34). Pour obtenir un schéma
conservatif, la matrice
![]() doit vérifier:
doit vérifier:
et doit tendre vers la jacobienne exacte
![]() .
En effet le problème linéarisé s'écrit:
.
En effet le problème linéarisé s'écrit:
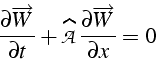
et correspond à un flux linéarisé
![]() .
Pour être conservatif, la solution doit vérifier les relations de
saut (5.4,5.5):
.
Pour être conservatif, la solution doit vérifier les relations de
saut (5.4,5.5):
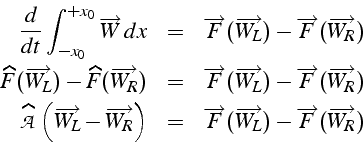
Pour les équations d'Euler, on peut utiliser pour ![]() ,
l'état de Roe, qui est la moyenne de Roe entre
,
l'état de Roe, qui est la moyenne de Roe entre ![]() et
et ![]()
![\begin{displaymath}
\widehat{W}=\left[\begin{array}{l}
\sqrt{\rho_{i}\rho_{i+1}}...
...}ht_{i+1}}{\sqrt{\rho_{i}}+\sqrt{\rho_{i+1}}}\end{array}\right]\end{displaymath}](img1004.png)
La matrice Jacobienne des flux de Roe s'écrit:
![\begin{displaymath}
\mathcal{\widehat{A}}=\left[\begin{array}{ccc}
0 & 1 & 0\\
...
...{\gamma-1}\widehat{c}^{2} & \widehat{u}\gamma\end{array}\right]\end{displaymath}](img1005.png)
Sa décomposition en valeurs propres s'écrit:
avec
![\begin{displaymath}
\Lambda=\left[\begin{array}{ccc}
u & 0 & 0\\
0 & u+c & 0\\
0 & 0 & u-c\end{array}\right]\end{displaymath}](img1007.png)
![\begin{displaymath}
\mathcal{R}=\left[\begin{array}{ccc}
1 & 1 & 1\\
u & u+c & u-c\\
\frac{1}{2}u^{2} & h+u+c & h-u+c\end{array}\right]\end{displaymath}](img1008.png)
![\begin{displaymath}
\mathcal{R}^{-1}=\left[\begin{array}{ccc}
1-\frac{1}{2}r_{2}...
...ac{1}{2}r_{1}-\frac{1}{2c} & \frac{1}{2v_{2}}\end{array}\right]\end{displaymath}](img1009.png)
avec
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Le flux de Roe s'écrit alors
![\begin{displaymath}
F_{i+1/2}^{Roe}=\frac{1}{2}\left[F(W_{i+1})+F(W_{i})\right]-...
...cal{\left\vert\widehat{A}\right\vert}\left(W_{i+1}-W_{i}\right)\end{displaymath}](img1014.png)
Ce schéma de Roe est à la base de nombreux schémas numériques pour les écoulements compressibles.