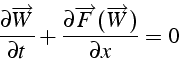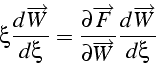suivant: 5.2 Tube à choc monter: 5. Modélisation numérique des précédent: 5. Modélisation numérique des Table des matières
Nous avons vu que les équations d'Euler régissant l'écoulement adiabatique non visqueux d'un fluide parfait s'écrivent sous la forme
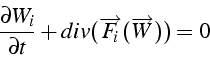
où
![]() est le vecteur d'état, et
est le vecteur d'état, et
![]() le vecteur
flux associé:
le vecteur
flux associé:
![\begin{displaymath}
\overrightarrow{F}_{\rho}=\left[\begin{array}{c}
\rho u\\
\...
...rray}{c}
\rho uv\\
\rho v^{2}+p\\
\rho vw\end{array}\right]\,\end{displaymath}](img736.png)
![\begin{displaymath}
\overrightarrow{F}_{w}=\left[\begin{array}{c}
\rho uw\\
\rh...
...{c}
\rho uh_{t}\\
\rho vh_{t}\\
\rho wh_{t}\end{array}\right]\end{displaymath}](img737.png)
où on a noté
![]() l'énergie totale par unité
de masse, et
l'énergie totale par unité
de masse, et
![]() l'enthalpie
totale par unité de masse.
l'enthalpie
totale par unité de masse.
A ces équations on ajoute l'équation d'état des gaz parfaits:
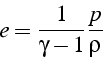
Dans le cas d'un écoulement uni-dimensionnel, elles s'écrivent:
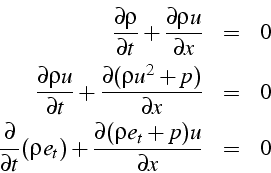
soit sous forme matricielle:
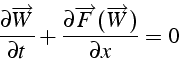
En introduisant la matrice jacobienne des flux: i.e. la dérivée du
vecteur flux
![]() par rapport
au vecteur d'état
par rapport
au vecteur d'état
![]()
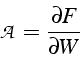
cette équation s'écrit sous la forme quasi-linéaire suivante:
Un calcul formel fournit l'expression de cette Jacobienne
![\begin{displaymath}
\mathcal{A}=\left[\begin{array}{ccc}
0 & 1 & 0\\
\frac{\gam...
...ma}{2}u^{2}+\frac{1}{\gamma-1}c^{2} & u\gamma\end{array}\right]\end{displaymath}](img744.png)
où ![]() est la vitesse du fluide (supposée
est la vitesse du fluide (supposée ![]() ), et
), et
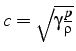 la célérité du son.
la célérité du son.
Cette matrice possède 3 valeurs propres réelles
ce qui traduit la présence de 3 courbes caractéristiques le long desquelles se propagent les perturbations.
Ces équations forment donc un système hyperbolique non linéaire. En
notant ![]() la matrice des vecteurs propres à droite
la matrice des vecteurs propres à droite
![]() :
:
la diagonalisation de ![]() s'écrit:
s'écrit:
où ![]() est la matrice diagonale des vecteurs propres
est la matrice diagonale des vecteurs propres ![]() .
En multipliant l'équation (5.1) par
.
En multipliant l'équation (5.1) par
![]() ,
on obtient:
,
on obtient:
On introduit le changement de variable
et le vecteur
![]() est appelé “variables
caractéristiques”. Le système d'équations transformé est appelé
“équations caractéristiques”:
est appelé “variables
caractéristiques”. Le système d'équations transformé est appelé
“équations caractéristiques”:
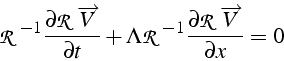
Dans le cas de petites perturbations, on peut simplifier ce système
en considérant que la matrice ![]() est constante ainsi que
les valeurs propres
est constante ainsi que
les valeurs propres ![]() :
:
Ce système caractéristique est un système de 3 équations scalaires indépendantes de type advection:
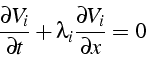
Cette équation traduit le fait que la composante ![]() est constante
le long de la droite caractéristique de pente
est constante
le long de la droite caractéristique de pente
![]() ,
i.e.:
,
i.e.:
La solution générale de (5.3) est donc une combinaison linéaire
de ces ondes caractéristiques, soit en revenant aux variables d'état
![]() :
:
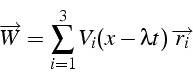
Les perturbations de la solution se propagent donc le long de ces directions caractéristiques.
Dans le cas non-linéaire, la matrice ![]() n'est plus constante,
et l'analyse précédente n'est plus exacte. On peut cependant la considérer
comme une approximation au premier ordre et en déduire les propriétés
de la solution. Le système hyperbolique (5.1) possède 3 valeurs
propres
n'est plus constante,
et l'analyse précédente n'est plus exacte. On peut cependant la considérer
comme une approximation au premier ordre et en déduire les propriétés
de la solution. Le système hyperbolique (5.1) possède 3 valeurs
propres
![]() , qui dépendent
de la solution
, qui dépendent
de la solution
![]() . Associées à ces 3 valeurs propres,
on a des courbes caractéristiques
. Associées à ces 3 valeurs propres,
on a des courbes caractéristiques
![]() de pente
de pente ![]() qui sont aussi fonctions de la solution
qui sont aussi fonctions de la solution
![]() .
Le long de ces caractéristiques se propagent les perturbations de
la solution sous forme d'ondes non-linéaires.
.
Le long de ces caractéristiques se propagent les perturbations de
la solution sous forme d'ondes non-linéaires.
![\includegraphics[width=0.8\textwidth]{CHAP5/perturb}](img767.png)
Considérons une perturbation située en ![]() à l'instant
à l'instant ![]() . Notons
. Notons
![]() la vitesse de propagation de la perturbation,
la vitesse de propagation de la perturbation, ![]() l'état
du fluide à gauche (left) et
l'état
du fluide à gauche (left) et ![]() l'état à droite (right). La
solution
l'état à droite (right). La
solution
![]() vérifie les équations d'Euler
vérifie les équations d'Euler
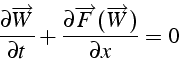
En intégrant cette équation sur un domaine
![]() autour
de la perturbation, on obtient l'équation:
autour
de la perturbation, on obtient l'équation:
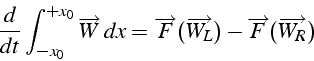
D'autre part si ![]() est grand devant
est grand devant ![]() , la variation
temporelle de
, la variation
temporelle de
![]() dans
dans
![]() s'écrit:
s'écrit:
![\begin{displaymath}
\int_{-x_{0}}^{+x_{0}}\overrightarrow{W}(t+dt)\, dx-\int_{-x...
...[\overrightarrow{W_{L}}x_{0}+\overrightarrow{W_{R}}x_{0}\right]\end{displaymath}](img775.png)
d'où:
On retrouve les relations de saut d'Hugoniot:
qui relie la vitesse de propagation de la perturbation ![]() à l'état
de part et d'autre de la perturbation
à l'état
de part et d'autre de la perturbation
![]() et
et
![]() . Cette vitesse de propagation
. Cette vitesse de propagation ![]() n'est
donc pas quelconque. En effectuant une analyse de perturbation au
premier ordre, i.e. en développant
n'est
donc pas quelconque. En effectuant une analyse de perturbation au
premier ordre, i.e. en développant
![]() au premier ordre au voisinage de
au premier ordre au voisinage de
![]() :
:
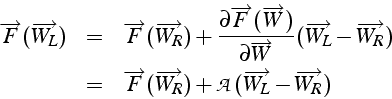
ce qui fournit la relation de saut pour une petite perturbation
Clairement cette relation montre que le saut
![$\left[\overrightarrow{W_{L}}-\overrightarrow{W_{R}}\right]$](img783.png) doit être proportionnel à un vecteur propre
doit être proportionnel à un vecteur propre
![]() de
de ![]() , et que la vitesse de propagation
, et que la vitesse de propagation ![]() est la valeur
propre
est la valeur
propre ![]() de
de ![]() associée. Les valeurs possibles
de
associée. Les valeurs possibles
de ![]() sont donc
sont donc ![]() .
.
Les relations de saut d'Hugoniot (5.5) s'écrivent:
Ces relations traduisent le bilan de la masse, la quantité de mouvement
et de l'énergie dans un repère lié au choc, i.e. se déplaçant à la
vitesse ![]() de propagation de la perturbation. Pour
de propagation de la perturbation. Pour ![]() , on retrouve
les équations du choc droit stationnaire, qui correspond à la valeur
propre
, on retrouve
les équations du choc droit stationnaire, qui correspond à la valeur
propre ![]() (i.e. une vitesse sonique dans le choc).
(i.e. une vitesse sonique dans le choc).
Il existe 3 types de discontinuité possible dans ce système d'équations d'Euler
![\includegraphics[width=1\textwidth]{CHAP5/contact}](img806.png)
![\includegraphics[width=1\textwidth]{CHAP5/choc}](img807.png)
![\includegraphics[width=1\textwidth]{CHAP5/detente}](img808.png)