suivant: Bibliographie monter: 5. Modélisation numérique des précédent: 5.3 Méthodes numériques Table des matières
Dans le cas d'un écoulement de fluide réel, il faut tenir compte de la viscosité du fluide et des échanges de chaleur par conduction, ou rayonnement.
Pour tenir compte de la viscosité du fluide, on introduit le tenseur
des contraintes visqueuses
![]() , qui pour
un fluide newtonien de viscosité
, qui pour
un fluide newtonien de viscosité ![]() s'écrit:
s'écrit:
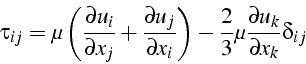
soit
![\begin{displaymath}
\overline{\overline{\tau}}=\mu\left[\overline{\overline{grad...
...div(\overrightarrow{u})\overline{\mathcal{\overline{I}}}\right]\end{displaymath}](img1018.png)
Les équations de bilan pour un écoulement compressible d'un fluide visqueux s'écrivent alors:
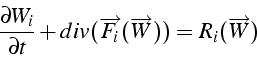
où
![]() représentent les termes sources dans
les équations de bilan de la masse, de la quantité de mouvement et
de l'énergie
représentent les termes sources dans
les équations de bilan de la masse, de la quantité de mouvement et
de l'énergie
Les nombres sans dimension caractéristiques sont