Introduction

Introduction à l’utilisation du calcul formel et du calcul numérique pour modéliser la cinématique et la dynamique de solides indéformables, calculer les trajectoires et les visualiser en 3D. L’objectif n’est pas de programmer, mais de savoir utiliser des fonctions d’une bibliothéque en tant qu’outils pour résoudre complétement (en général numériquement) des problèmes de cinématique et de dynamique des solides indéformables. En particulier, la résolution numérique est simplifiée par l’utilisation de fonctions déja programmées.

Cinématique d’une nacelle de manége

Comme premier exemple, on étudie la cinématique simplifié d’une nacelle de manége, en particulier pour mettre en évidence l’importance de la force centrifuge.

Cinématique d’une trottinette éléctrique

On étudie la cinématique d’une trottinette électrique dans son mouvement général, puis on l’analyse dans le cas simple d’une trajectoire droite, puis dans le cas plus complexe d’une trajectoire circulaire. On en déduit à la fin des propriétés de stabilité du système.

Modelisation d’une toupie

Utilisation de calcul symbolique sous jupyter notebook pour modéliser, simuler et visualiser le mouvement de précésion d’une toupie (mouvement de Lagrange).

Mouvement d’une perle sur un cerceau

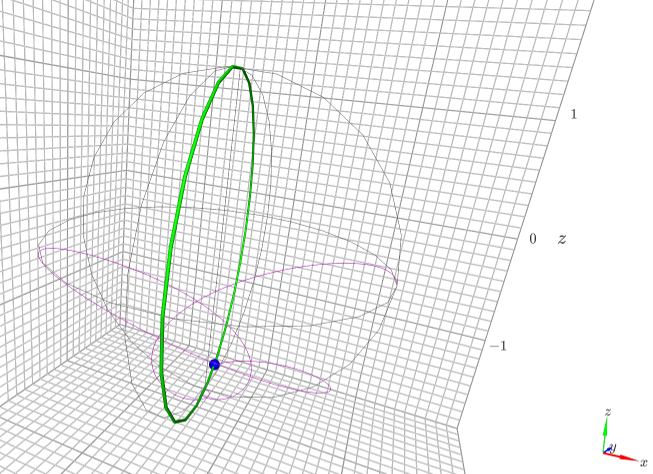
TP virtuel (coté étudiant) pour l’étude du mouvement d’une perle sur un cerceau en rotation.

A partir du formalisme classique de Newton, on redonne les équations du mouvement que l’on résoud ensuite numériquement avec des paramêtres propres à chaque étudiant. On demande ensuite à l’étudiant de faire une étude paramêtrique du mouvement en fonction de la position initiale de la perle. L’objectif est d’étudier les positions d’équilibres du système et de caractériser le mouvement lorsque la position initiale est plus ou moins proche de la position d’équilibre.

Documentation

• calcul symbolique Sympy:

• bibliotheque Sympy de Mechanique classique:

• visualisation 3D k3d: