"Mécanique des solides indéformables"

Dpt de mécanique

consignes

Executer toujours tout le notebook depuis le début (en appuyant sur executer)

pour les TP

Executer le notebook et suivez les instructions. A la fin appuyer sur submit pour soumettre votre travail.

ATTENTION le travail demandé est un travail personnel. Tout étudiant est tenu de respecter les règles relatives au plagiat. Constitue notamment du plagiat le fait de remettre un travail copié en totalité ou en partie d'un autre étudiant (avec ou sans l'accord de cet autre étudiant)

Votre travail sera soumis à un système de détection de plagiat, et vous risquez donc d'être sanctionné en cas de plagiat.

en cas de problème

Tout d'abord, redémarrez le noyau (dans la barre de menus, sélectionnez Kernel -> Restart), puis exécutez toutes les cellules (dans la barre de menus, sélectionnez Cellule -> Run All).

remplir la cellule suivante

Ecrire votre nom , prénom et votre numéro d'étudiant ci-dessous Le numéro d'étudiant doit etre un entier !!!

In [15]:
NOM = "BUFFAT"
PRENOM = "Marc"
NUMERO_ETUDIANT = 12345
if type(NUMERO_ETUDIANT) is not int :
    print("ERREUR: numéro d'étudiant non spécifié!!!")

Mouvement d'une perle sur un cerceau

Marc Buffat département mécanique Lyon 1

Objectif

Etude du mouvement d'une bille sur un cerceau qui tourne avec une vitesse constante $\omega$ autour de $Oz$

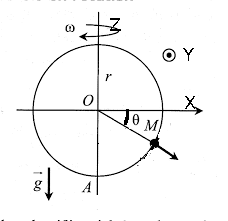
bille

Le cerceau a un rayon $R$ et on considère que la bille a une masse $M$ à la position B sur ce cerceau avec un angle $\theta$ et glisse sans frottement. A l'instant initiale la bille est lachée à une position initiale $\theta = \theta_0$ avec $\dot{\theta}=0$

L'objectif est de déterminer la position de la bille en utilisant la formalisme du cours. Dans une première partie, on vous redonne le formalisme du cours pour obtenir les équations du mouvement. Ensuite chaque étudiant aura des valeurs particulières à traiter pour résoudre numériquement le système. Le travail demandé est l'analyse des résultats de la simulation avec une visualisation du mouvement de la bille.

Un petit compte rendu est attendu pour chaque étudiants à la fin du notebook.

In [16]:
%matplotlib inline
import numpy as np
import sympy as sp
import k3d
import matplotlib.pyplot as plt
# bibliotheque mecanique
from sympy.physics.mechanics import dynamicsymbols, Point, ReferenceFrame
from sympy.physics.mechanics import Particle, RigidBody, inertia
from sympy.physics.mechanics import linear_momentum, angular_momentum
from sympy.physics.vector import time_derivative,dot
from sympy.physics.vector import init_vprinting
init_vprinting(use_latex='mathjax', pretty_print=False)
#
from IPython.display import display, Markdown, clear_output
def printmd(string):
    display(Markdown(string))
# test si numero étudiant spécifier
try: NUMERO_ETUDIANT
except NameError: NUMERO_ETUDIANT = None 
if type(NUMERO_ETUDIANT) is not int :
    printmd("## ERREUR: numéro d'étudiant non spécifié!!!")
    NUMERO_ETUDIANT = 12345
    NOM = "toto"
    PRENOM = "toto"
    #raise AssertionError("NUMERO_ETUDIANT non défini")
# parametres spécifiques
_uid_    = NUMERO_ETUDIANT
np.random.seed(_uid_)
printmd("## Etudiant {} {}  id={}".format(NOM,PRENOM,NUMERO_ETUDIANT))
# parametres
_R = np.round(0.1+1*np.random.rand(),2)
_M = np.round(0.1+1*np.random.rand(),2)
_g = 9.81
_omega = np.round(np.sqrt(2*_g/_R),2)
printmd("# Paramétres de l'étude: R={} M={} omega={} g={}".format(_R,_M,_omega,_g))

Etudiant BUFFAT Marc id=12345

Paramétres de l'étude: R=1.03 M=0.42 omega=4.36 g=9.81

Modele mécanique

  • on définit les parametres du problèmes
  • on définit les degrés de liberté
  • on définit les repères

  • on applique le PFD à la bille:

    variation de la quantité de mouvement = somme des forces appliquées

    $$\frac{d}{dt}(M V_B)|R_0 = \sum forces $$

parametres du problème

In [17]:
# parametres du problème: rayon masse du cerceau position masse 
R, M, g, omega = sp.symbols('R M g omega')
# degrés de liberté
theta  = dynamicsymbols('theta')
thetap = dynamicsymbols('theta',level=1)
t = sp.symbols('t')

Repère et position

In [18]:
# reperes et points
O = Point('O')
R0 = ReferenceFrame('R_0')
# cerceau
R1 = ReferenceFrame('R_1')
R1.orient(R0,'Axis',[omega*t, R0.z])
# bille 
R2 = ReferenceFrame('R_2')
R2.orient(R1,'Axis',[theta, R1.y])
# position bille B
B = Point('B')
B.set_pos(O,R*R2.x)

calcul quantité de mouvement dans R0

In [19]:
# definition et calcul des vitesses
O.set_vel(R0,0.)
B.set_vel(R2,0.)
B.v2pt_theory(O,R0,R2)
bille   = Particle('bille',B,M)
# quantite de mouvement de la bille
display(bille.linear_momentum(R0))
$\displaystyle M R \omega \operatorname{cos}\left(\theta\right)\mathbf{\hat{r_2}_y} - M R \dot{\theta}\mathbf{\hat{r_2}_z}$

PFD pour la bille en B

les forces appliquées sont:

  • les réactions du cerceau (sans composante suivant R2.z)
  • le poids
In [20]:
# dérivée de la quantité de mouvement
QB = time_derivative(bille.linear_momentum(R0),R0)
QB
Out[20]:
$\displaystyle (- M R \omega^{2} \operatorname{cos}^{2}\left(\theta\right) - M R \dot{\theta}^{2})\mathbf{\hat{r_2}_x} - 2 M R \omega \operatorname{sin}\left(\theta\right) \dot{\theta}\mathbf{\hat{r_2}_y} + (- M R \omega^{2} \operatorname{sin}\left(\theta\right) \operatorname{cos}\left(\theta\right) - M R \ddot{\theta})\mathbf{\hat{r_2}_z}$
In [21]:
# somme des forces
Rbx,Rby = sp.symbols('R_bx R_by ')
FB = Rbx*R2.x + Rby*R2.y - M*g*R0.z
FB
Out[21]:
$\displaystyle R_{bx}\mathbf{\hat{r_2}_x} + R_{by}\mathbf{\hat{r_2}_y} - M g\mathbf{\hat{r_0}_z}$
In [22]:
# equations du mouvement
eq1=(QB-FB).dot(R2.x)
display(sp.Eq(eq1,0))
eq2=(QB-FB).dot(R2.y)
display(sp.Eq(eq2,0))
eq3=(QB-FB).dot(R2.z)
display(sp.Eq(eq3,0))
$\displaystyle - M R \omega^{2} \operatorname{cos}^{2}\left(\theta\right) - M R \dot{\theta}^{2} - M g \operatorname{sin}\left(\theta\right) - R_{bx} = 0$
$\displaystyle - 2 M R \omega \operatorname{sin}\left(\theta\right) \dot{\theta} - R_{by} = 0$
$\displaystyle - M R \omega^{2} \operatorname{sin}\left(\theta\right) \operatorname{cos}\left(\theta\right) - M R \ddot{\theta} + M g \operatorname{cos}\left(\theta\right) = 0$

Simulation numérique

on résoud numériquement le système précédent en fixant la valeur des parametres:

In [23]:
valnum = [(R,_R), (M,_M), (g,_g), (omega, _omega)]
display(valnum)
display(sp.Eq(eq1.subs(valnum),0))
display(sp.Eq(eq2.subs(valnum),0))
display(sp.Eq(eq3.subs(valnum),0))
$\displaystyle \left[ \left( R, \ 1.03\right), \ \left( M, \ 0.42\right), \ \left( g, \ 9.81\right), \ \left( \omega, \ 4.36\right)\right]$
$\displaystyle - R_{bx} - 4.1202 \operatorname{sin}\left(\theta\right) - 8.22355296 \operatorname{cos}^{2}\left(\theta\right) - 0.4326 \dot{\theta}^{2} = 0$
$\displaystyle - R_{by} - 3.772272 \operatorname{sin}\left(\theta\right) \dot{\theta} = 0$
$\displaystyle - 8.22355296 \operatorname{sin}\left(\theta\right) \operatorname{cos}\left(\theta\right) + 4.1202 \operatorname{cos}\left(\theta\right) - 0.4326 \ddot{\theta} = 0$

question

Dans le système précédent :

  • combien y a t-il d'inconnues, et lequelles?
  • quelle est l'équation différentielle à résoudre pour pouvoir obtenir la solution?
  • quelle est l'interprétation mécanique de cette équation ?
  • que faut -il se donner en plus pour pouvoir la résoudre

Ecrire votre réponse dans la cellule ci-dessous

YOUR ANSWER HERE

résolution numérique fonction de $\theta_0$

On choisit la position initiale de la perle $\theta_0$ dans la cellule et on simule le mouvement.

Modifier la valeur dans la cellule et executer les cellules suivantes

travail demandée

pour différentes valeurs de $\theta_0$ ($0$,$\pi/4$,$5\pi/8$, $\pi/2$ , $3\pi/2$ , $\pi$, ..)

  • faites la simulation en executant les cellules suivantes
  • analyser le mouvement
  • tracer certaines quantités en fonction du temps
In [24]:
# choix de la position initiale
theta0=0.
# telmps de simulation
tmax = 4
In [25]:
# modèle numérique
from Bille import Bille
BI = Bille(t,[theta,thetap],[eq3.subs(valnum)],
           [B.pos_from(O).dot(R0.x).subs(valnum),B.pos_from(O).dot(R0.y).subs(valnum),B.pos_from(O).dot(R0.z).subs(valnum)],
           [bille.kinetic_energy(R0).subs(valnum),(M*g*B.pos_from(O).dot(R0.z)).subs(valnum)],
           _R, _omega) 
# resolution 
Y0 = [theta0,0.]
BI.solve(Y0,tmax)
In [26]:
# tracer de la solution 
plt.figure(figsize=(12,6))
plt.subplot(1,2,1)
plt.plot(BI.t,BI.THETA,label="$\\theta(t)$")
plt.plot(BI.t,BI.THETAP,label="$\dot{\\theta}(t)$")
plt.legend()
plt.title('solution fct de t')
plt.xlabel('t')
plt.subplot(1,2,2)
plt.plot(BI.XB,BI.YB)
plt.xlabel('X')
plt.ylabel('Y')
plt.title('trajectoire dans le plan (X,Y)')
plt.axis('equal');
In [27]:
# visualisation 3D du mouvement
BI.trace()
BI.trajectoire()

visualisation 3D du mouvement de la bille

analyse du mouvement

pour analyser le mouvement on pourra tracer les quantités suivantes issues du calcul

  • BI.t: les valeurs discretes du temps où la solution est calculée
  • BI.THETA, BI.THETAP: les valeurs de $\theta$ et $\dot{\theta}$
  • BI.XB, BI.YB, BI.ZB : les coordonnées de la bille dans R0
  • BI.EC, BI.EP: l'energie cinétique et potentielle

pour tracer une quantité en fonction du temps, par exemple BI.ZB

  plt.plot(BI.t,BI.ZB)
In [28]:
# YOUR CODE HERE
plt.plot(BI.t,BI.ZB)
Out[28]:
[<matplotlib.lines.Line2D at 0x7f39b99cc080>]

Bilan et compte rendu

Ecrire un compte rendu sur l'analyse du mouvement en fonction de $\theta_0$

Questions:

  • le système a t-il des positions d'équilibres et si oui lesquelles
  • les positions d'équilibre sont-elles stables ou instables

  • comment se comporte la bille en fonction des valeurs de $\theta_0$

    Ecrire un compte rendu dans la cellule suivante

YOUR ANSWER HERE

FIN