Outils de calcul formel et numérique pour

l'étude de la cinématique et dynamique des solides

Marc BUFFAT département mécanique, université Lyon 1

Contenu

In [1]:
%matplotlib inline
import numpy as np
import sympy as sp
import k3d
import matplotlib.pyplot as plt
from IPython.core.display import HTML
from IPython.display import display,Image
from sympy.physics.vector import init_vprinting
init_vprinting(use_latex='mathjax', pretty_print=False)

Objectifs

Utilisation d'un outil de calcul formel et de calcul numérique pour étudier la cinématique et la dynamique des solides, permettant de résoudre complètement le problème.

  • application de la démarche du cours
  • mise en équation en utilisant du calcul formel pour faciliter les calculs analytiques (changement de repère, projection, composition des mouvements,..)

  • résolution numérique des équations pour obtenir la solution

    ATTENTION ces outils ne sont pas une boite noir pour résoudre automatiquement les problèmes. Il faut comprendre la démarche pour pouvoir les utiliser à bon escient.

Python

Le langage de programmation Python sera utiliser pour manipuler ces outils. Ce n'est pas de la programmation, mais l'utilisation d'instructions Python (à la matlab) pour appeler des fonctions. Il faut cependant connaître un minimum de syntaxe du langage Python.

Python est un langage de programmation très générique et utilisé dans beaucoup de contexte différent.

  • On écrit chaque instruction sur une ligne et les instructions commencent au début de la ligne (sans espace avant) et se termine par un retour à la ligne
  • Python fait la différence entre majuscule et minuscule
  • Python encourage une programmation simple et lisible (utilisation des espaces pour aérer l'écriture)
  • Python est un langage non-déclaratif (contrairement au C, on ne déclare pas le type des variables)
  • Python est un langage interprété (comme matlab): les instructions sont exécutées au fur et à mesure
  • Python peut manipuler des nombres réels (float), entier (int), chaînes de caractère (string) (comme le C)
  • Mais aussi des listes d'objets (entre [..] [objet1, object2, ...]), des tableaux (array) ....
  • Python est un langage de programmation généraliste qui utilise intensément des bibliothèques
  • Pour cela on utilise la syntaxe: import mabib as nom pour importer la bibliothèque mabib avec un nom simplifié nom
  • Nous allons surtout utiliser les modules matplotlib, numpy pour le calcul numérique et sympy pour le calcul symbolique

Notebook IPython

On utilise un serveur web Jupyter avec des notebooks Ipython, qui permet à l'aide d'un simple navigateur web sur un PC, une tablette ou un smartphone d'utiliser ces bibliothèques pythonà distance.

Le notebook est une interface web riche qui permet d'associer du code, la réponse du code et du texte. Le document que l'on travaille est composé de cellules.

  • des cellules de code où on tape le code. On clique ensuite sur le bouton > executer pour executer la cellule.
  • des cellules de texte Markdown où on rentre du texte qui est ensuite affiché

ATTENTION en programmation l'ordre d'exécution des instructions est primordiale. Il faut donc exécuter les cellules dans l'ordre en cliquant sur exécuter du début à la fin du notebook et pas en déplaçant avec la souris dans le notebook.

Outils de calcul symbolique et numérique

Utilisation du langage de programmation Python et des notebooks Ipython

Utilisation de bibliothèques python spécialisées en calcul numérique:

  • numpy (documentation) (numerical python): pour le calcul numérique avec une manipulation simple de vecteurs et matrices (à la matlab)
  • matplotlib: pour le tracer de courbes en 2D

  • k3D : pour la visualisation 3D de trajectoires

    import numpy as np
import k3d
import matplotlib.pyplot as plt

et en calcul symbolique:

  • sympy symbolic python
  • vector bibliothèque sympy pour manipuler des vecteurs et des repères en 3D (projection, dérivation ..)

  • classical mechanics bibliothèque sympy pour l'étude de la cinématique et dynamique des solides

    import sympy as sp
from sympy.physics.mechanics import dynamicsymbols, Point, ReferenceFrame, RigidBody
from sympy.physics.vector import dot

    Attention en général quand on utilise une fonction d'une bibliothéque python, on préfixe en général la fonction par le nom (simplifié) de la bibliothéque

    np.cos(..)
sp.symbols(..)

Paramètres, Point et Référentiel

sous python, on va utiliser des variables (objets) dont la valeur est un symbole. Lors de la création, on doit définir comment sera affiché le symbole en fournissant la chaîne de caractère qui sera affichée. Par défaut sympy reconnaît les lettres grecques( i.e. 'alpha' sera affiché $\alpha$) et les indices (i.e. 'X_A' sera affiché $X_A$)

  • définitions des paramètres du problème

    • fonction sp.symbols() pour définit une variable symbolique

      alpha,L = sp.symbols('alpha L')

    • fonction dynamicsymbols pour définir un degré de liberté (fct de t)

      xa, ya = dynamicsymbols('x_a y_a')

  • définition d'un repère

    • fonction ReferenceFrame: definit un repère

      R1 = ReferenceFrame('R_1')

    • ensuite on utilise les fonctions (méthodes) associées pour positionner le repère (rotation par rapport à un autre repère) (orient)

      R1.orient(R0,'Axis',[psi, R0.z])

  • définition d'un point

    • fonction Point: définit un point dans l'espace

      A = Point('A')

    • ensuite on utilise les fonctions (méthodes) associées pour positionner le point par rapport à un autre point: set_pos

      pour positionner le point A: on écrit : $\overrightarrow{OA} = r \overrightarrow{R_1.x}$

      A.set_pos(O,r*R1.x)

Composition des mouvements

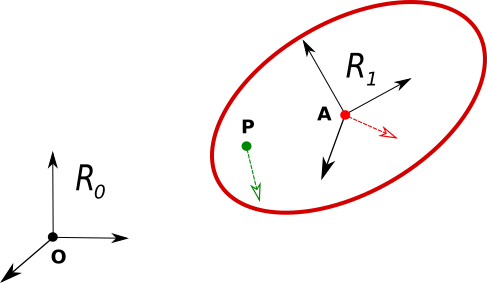composition_mvt Dans un référentiel fixe $R_0$ d'origine O, on étudie la cinématique (mouvement) d'un solide S définit par un point A et un repère $R_1$ lié à S. On a s'intéresse à la cinématique d'un point P (observateur) dans $R_1$ connaissant la cinématique de A en utilisant la composition des mouvements.

composition des vitesses $V$

On veut calculer la vitesse en P connaissant la vitesse en A. On distingue 2 cas:

  • le point P est mobile dans $R_1$ ( 1 point theory: P n'appartient pas au solide S)
$$\underbrace{\overrightarrow{V}^{\,R_0}_P}_\textrm{V absolue} = \underbrace{\overrightarrow{V}^{\,R_1}_P}_\textrm{V relative} + \underbrace{\overrightarrow{V}^{\,R_0}_A + \overrightarrow{\Omega}_{R_1/R_0} \wedge \overrightarrow{AP}}_\textrm{V entraînement}$$
  • le point P est fixe dans $R_1$ ( 2 points theory: A et P appartiennent au solide S) $$\overrightarrow{V}^{\,R_0}_P = \overrightarrow{V}^{\,R_0}_A + \overrightarrow{\Omega}_{R_1/R_0} \wedge \overrightarrow{AP}$$

Les fonctions membres (méthodes) v1pt_theory et v2pt_theory de la classe Point font le calcul symbolique

   # si P mobile dans R1, calcul V(P)/R0
   P.v1pt_theory(A,R0,R1)
   # et si P est fixe dans R1
   P.v2pt_theory(A,R0,R1)

composition des accélérations $\gamma$

  • le point P est mobile dans $R_1$ ( 1 point theory: P n'appartient pas au solide S)
\begin{eqnarray} \underbrace{\overrightarrow{\gamma}^{\,R_0}_P}_\textrm{absolue} & = & \underbrace{\overrightarrow{\gamma}^{\,R_1}_P}_\textrm{relative} + \underbrace{\overrightarrow{\gamma}^{\,R_0}_A + \dot{\overrightarrow{\Omega}}_{R_1/R_0} \wedge \overrightarrow{AP} + \overrightarrow{\Omega}_{R_1/R_0} \wedge \overrightarrow{\Omega}_{R_1/R_0} \wedge \overrightarrow{AP}}_\textrm{entraînement}\\ & + & \underbrace{2 \overrightarrow{\Omega}_{R_1/R_0} \wedge \overrightarrow{V}^{\,R_1}_P}_\textrm{coriolis}\\ \end{eqnarray}
  • le point P est fixe dans $R_1$ ( 2 points theory: A et P appartiennent au même solide S)
$$\overrightarrow{\gamma}^{\,R_0}_P = \overrightarrow{\gamma}^{\,R_0}_A + \dot{\overrightarrow{\Omega}}_{R_1/R_0} \wedge \overrightarrow{AP} + \overrightarrow{\Omega}_{R_1/R_0} \wedge \overrightarrow{\Omega}_{R_1/R_0} \wedge \overrightarrow{AP} $$

Les fonctions membres (méthodes) a1pt_theory et a2pt_theory de la classe Point font le calcul symbolique

 # si P mobile dans R1
 P.a1pt_theory(A,R0,R1)
 # et si P et A sont fixes dans R1
 P.a2pt_theory(A,R0,R1)

opération sur les vecteurs (et expression symbolique)

  • dot produit scalaire $\vec{A} . \vec{B}$
  • cross produit vectoriel $\vec{A}\wedge\vec{B}$
  • express projection dans un repère
  • simplify simplification
  • subs substitution (argument dictionnaire (nom,valeur))

Dynamique

  • RigidBody() définit un solide à partir de sa masse M, de son centre de gravité G, d'un référentiel associé $R_3$ et de sa matrice d'inertie IG en un point

  • inertia() calcul des matrices d'inertie

    IG = inertia(R2,I2,I2,I1)
solide = RigidBody('Solide',G,R3,M,(IG,G))

    On utilise ensuite les fonctions membres (méthodes) pour calculer les quantités dynamique:

    • la quantité de mouvement linear_momentum, le moment cinétique angular_momentum, l'énergie cinétique kinetic_energy ....

Exemple: modélisation d'un solide en translation/rotation

On veut modéliser un solide en translation dans le plan et en rotation autour de l'axe vertical.

Dans un repère fixe $(O,R_0)$, on étudie le mouvement d'un solide de masse M, de centre de gravité G (de coordonnées $x_g,y_g,0$). On note $R_1$ le référentiel lié au solide dans lequel la matrice d'inertie $I_G$ en G s'écrit: $$ I_G = \left[ \begin{matrix}I_1 & 0 & 0\\ 0 & I_2 & 0\\0 & 0 & I_3 \end{matrix} \right]$$ Le référentiel $R_1$ est obtenu à partir de $R_0$ par une rotation d'angle $\theta$ autour de $R_0.z$.

In [2]:
# bibliothéques utilisées
import sympy as sp
from sympy.physics.mechanics import dynamicsymbols, Point, ReferenceFrame, RigidBody, inertia
# parametres
M, I1, I2, I3, t = sp.symbols('M I_1 I_2 I_3 t')
# degré de liberté (fct de t)
xg, yg, theta = dynamicsymbols('x_g y_g theta')
# repere fixe
O  = Point('O')
R0 = ReferenceFrame('R_0')
O.set_vel(R0,0.)
# point et repère lié au solide (rotation /)
G = Point('G')
G.set_pos(O, xg*R0.x + yg*R0.y)
R1 = ReferenceFrame('R_1')
R1.orient(R0,'Axis',[theta,R0.z])
G.set_vel(R1,0)
# momement d'inertie
IG = inertia(R1,I1,I2,I3)
# solide S
S = RigidBody('S',G, R1, M, (IG,G))

vitesse, accélération, quantité de mouvement, moment cinétique

En utilisant les calculs précédents, calculez et afficher avec la fonction display()

  • la vitesse de G par dérivation des composantes (utilisation de la méthode .diff(t))
  • la méthode .vit(frame)
  • la vitesse exprimée dans R1 avec .express(frame)
  • la quantité de mouvement .linear_momentum(frame)
  • la vitesse angulaire .angular_momentum(point,frame)
  • l'énergie cinétique .kinetic_energy(frame)
  • l'accélération par dérivation avec .diff(t,frame)
  • simplifier avec .simplify()
  • l'accélération avec la méthode .acc(frame)
In [3]:
# entrez vos calculs ici

Calcul numérique

  • bibliothéque numpy (documentation)
  • bibliothéque matplotlib (documentation) pour le tracé de courbes
  • utilisation de la notation vectorielle à la matlab

  • mais attention indice à partir de 0 (comme en C, on compte à partir de 0)

     X = np.array([1,2,3])
 Y = np.cos(X)*X*
 print("dimension de X : ",X.size)
 print("1er     element: ",X[0),Y[0])
 print("dernier element: ",X[2],Y[2])
 plt.plot(X,Y)

  • lambdify conversion expression symbolique en fonction python

      u = A*cos(omega*t+phi)
  U = sp.lambdify([t],u.subs([(A,2.0),(omega,2*sp.pi/3.),(phi,sp.pi/2)]))
  T = np.linspace(0,3,100)
  Y = U(T)
  plt.plot(T,Y)

application

Le solide S correspond à un disque plein de rayon $𝑅=4$, de masse $𝑀=2$.

La matrice d'inertie vaut: $$ 𝐼_𝐺 = 𝑀𝑅^2 \begin{bmatrix} 1/4& 0& 0 \\ 0& 1/4 &0 \\ 0 & 0 &1/2 \end{bmatrix} $$ calculez la valeur de la vitesse pour une trajectoire de G rectiligne et une rotation constante: $$ 𝑥_𝑔(𝑡) = 3𝑡, 𝑦_𝑔(𝑡) = 3𝑡, \theta(𝑡)=2𝑡 $$

Pour cela utiliser la fonction .subs() avec comme argument une liste de substitution: [(nom1,val2),(nom2,val2),..]

In [4]:
# entrez vos calcul ici

Conclusion

En fin d'analyse, il faut écrire une conclusion sur l'étude. Pour cela on entera du texte dans une cellule Markdown en utilisant les règles de formatage suivantes. Pour modifier une cellule de texte, il faut passer en mode édition en double cliquant sur la cellule.

Règles de formattage du texte

Il est possible de mettre en page (un minimum) le texte dans une cellule Markdown.

Ces règles sont assez sommaires, mais suffisent en général pour ce qu'on veut écrire. Pour une mise en page plus complète, il faudra utiliser des logiciels tiers (Latex, openoffice, etc...)

italique, gras :

On utilise le caractère * pour mettre du texte en :

  • italique : texte --> texte
  • gras : texte --> texte

Saut de ligne, nouveau paragraphe : Pour commencer une nouvelle ligne, il faut ajouter deux espaces à la fin d'une ligne. Pour commencer un nouveau paragraphe, il faut sauter deux lignes.

Titres Pour inclure un titre, il faut utiliser le caractère # en début de ligne. Tout le reste de la ligne sera alors formaté comme un titre (grande police, gras).

Si on utilise plusieurs caractères en début de ligne, le niveau de titre diminue :

-  # --> titre principal
-  ## --> sous-titre
-  ### --> sous-sous-titre
-  etc...

Entrez ici votre analyse

mon analyse

FIN