Modélisation d'un manège

Marc BUFFAT département mécanique, université Lyon 1 manege_nacelle

In [1]:
%matplotlib inline
import numpy as np
import sympy as sp
import k3d
import matplotlib.pyplot as plt
from IPython.core.display import HTML
from IPython.display import display,Image
from sympy.physics.vector import init_vprinting
init_vprinting(use_latex='mathjax', pretty_print=False)

Modélisation d'une nacelle de manège

On s'intéresse à la cinématique d'une nacelle de manège assimilée à une boule de centre A et de rayon r, et entrainée en rotation par un bras AB de longueur L et fixé en B. On a un passager de masse M dans la nacelle, qui représente l'essentiel du poids.

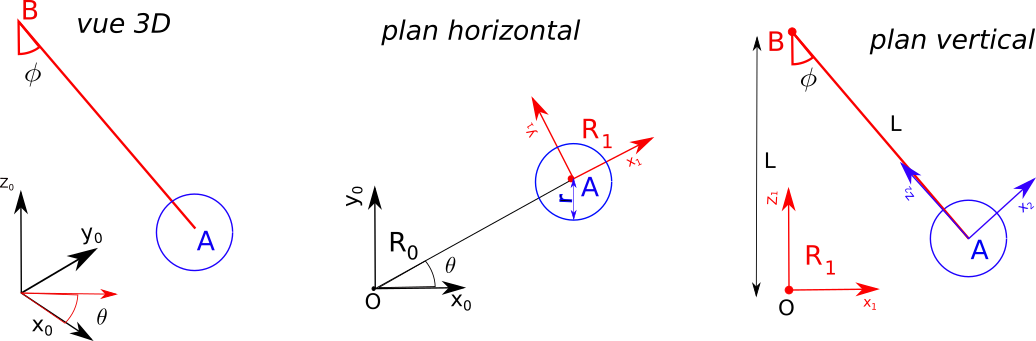
manege

On note $R_0$ le repère fixe d'origine O. On note $R_1$ le repére obtenu à partir de $R_0$ par rotation $\theta$ autour de la vertical $R_0.z$ et on note $\phi$ l'angle du cable avec la verticale. On note $R_2$ le repère lié à la nacelle avec $R_2.z$ orienté suivant la direction du bras.

Les paramêtres sont:

  • la longueur $L=AB$ du bras, l'accélération de la pesanteur g et la masse $M$ du passager
  • la position de la nacelle est donnée par les 2 angles $\phi$ et $\theta$

Paramétrage du problème

In [2]:
# bibliothéque utilisée
import sympy as sp
from sympy.physics.mechanics import dynamicsymbols, Point, ReferenceFrame
In [3]:
# definition des parametres et des ddl
L, g, M,  t = sp.symbols("L g M t")
theta, phi = dynamicsymbols("theta phi")

définition des repères

  • 3 repères R0, R1, R2
  • 3 points O, A, B
In [4]:
# definition des points et repère
O = Point("O")
R0 = ReferenceFrame("R_0")
B = Point("B")
B.set_pos(O,L*R0.z)
R1 = ReferenceFrame("R_1")
R1.orient(R0,'Axis',[theta,R0.z])
R2 = ReferenceFrame("R_2")
R2.orient(R1,'Axis',[-phi,R1.y])
A = Point("A")
A.set_pos(B,-L*R2.z)

projection

calculez dans la cellule suivante la position de A dans le repère R0 en utilisant .pos_from() et .express()

In [5]:
print("Position de A dans R0")

Position de A dans R0

Cinématique: calcul des vitesses

on calcule la vitesse de A par composition des vitesses de même que l'accélération

In [6]:
O.set_vel(R0,0)
B.set_vel(R0,0)
A.set_vel(R2,0)
VA = A.v1pt_theory(B,R0,R2)
print("Vitesse de A / R0")
display(VA)

Vitesse de A / R0
$\displaystyle L \dot{\phi}\mathbf{\hat{r_2}_x} + L \operatorname{sin}\left(\phi\right) \dot{\theta}\mathbf{\hat{r_2}_y}$
In [7]:
GA = A.a1pt_theory(B,R0,R2)
print("Accélération de A / R0")
display(GA)

Accélération de A / R0
$\displaystyle (- L \operatorname{sin}\left(\phi\right) \operatorname{cos}\left(\phi\right) \dot{\theta}^{2} + L \ddot{\phi})\mathbf{\hat{r_2}_x} + (L \left(\operatorname{sin}\left(\phi\right) \ddot{\theta} + \operatorname{cos}\left(\phi\right) \dot{\phi} \dot{\theta}\right) + L \operatorname{cos}\left(\phi\right) \dot{\phi} \dot{\theta})\mathbf{\hat{r_2}_y} + (L \operatorname{sin}^{2}\left(\phi\right) \dot{\theta}^{2} + L \dot{\phi}^{2})\mathbf{\hat{r_2}_z}$

projection

calculez dans la cellule suivante la vitesse et l'accélération de A dans le repère R0 en utilisant .vel(), .acc(), .express() et .simplify()

In [8]:
# vitesse de A dans R0

# accélération de A dans R0

Cas stationnaire

Pour simplifier on suppose que l'angle $phi=\phi_0$ reste constant et que la vitesse de rotation du manège est constante: $\dot{\theta}=\omega$ d'où $\theta=\omega t$ (régime stationnaire du manège).

On définit ses conditions sous la forme d'un dictionnaire python (nom,val) pour substituer ensuite dans les expressions précédentes

In [9]:
omega, phi0 = sp.symbols('omega phi_0')
cdts = [(phi,phi0),(theta,omega*t)]
In [10]:
VVA = VA.subs(cdts).simplify()
print("vitesse tangentielle")
display(VVA)

vitesse tangentielle
$\displaystyle L \omega \operatorname{sin}\left(\phi_{0}\right)\mathbf{\hat{r_2}_y}$
In [11]:
GGA = GA.express(R1).subs(cdts).simplify()
print("acceleration centripéde;")
display(GGA)

acceleration centripéde;
$\displaystyle - L \omega^{2} \operatorname{sin}\left(\phi_{0}\right)\mathbf{\hat{r_1}_x}$

Etude dynamique

En appliquant le principe fondamentale de la dynamique au point A, soumis à la force de gravité $\vec{P}$ et à la tension $\vec{T_c}$ du bras. $$ M \vec{\gamma} = \vec{P} + \vec{T_c} $$ ou $$ \vec{P} + \vec{T_c} - M \vec{\gamma} $$

On peut en déduire la valeur de la tension T et l'angle $\phi_0$ du bras.

In [12]:
T = sp.symbols('T')
Tc = T*R2.z
P = - M*g*R1.z
Bilan = Tc + P - M*GGA
Bilan = Bilan.express(R1).subs(cdts)
print("Bilan :")
display(Bilan)

Bilan :
$\displaystyle (L M \omega^{2} \operatorname{sin}\left(\phi_{0}\right) - T \operatorname{sin}\left(\phi_{0}\right))\mathbf{\hat{r_1}_x} + (- M g + T \operatorname{cos}\left(\phi_{0}\right))\mathbf{\hat{r_1}_z}$
In [13]:
# solution
TT = sp.solve(Bilan.dot(R1.x),T)[0]
display(sp.Eq(T,TT))
Phi0 = sp.solve(Bilan.dot(R1.z).subs(T,TT),phi0)[1]
display(sp.Eq(phi0,Phi0))
$\displaystyle T = L M \omega^{2}$
$\displaystyle \phi_{0} = \operatorname{acos}\left(\frac{g}{L \omega^{2}}\right)$

Analyse

Dans le référentiel fixe, la nacelle est donc soumise à une accélération centripéde, due à la somme des forces de tension et gravité.

Mais pour le passager immobile dans la nacelle, il est en équilibre sous l'effet:

  • de son poids $M\vec{g}$
  • de la tension dans le bras $\vec{T}$
  • de la force centrifuge (opposée à l'accélération centripéde) $L\sin(\phi_0)M\omega^2 \vec{R_1}.x$

La force centripète et la force centrifuge sont exactement la même force, mais dans des directions opposées, car elles sont éprouvées à partir de cadres de référence différents. Un observateur dans un repère en rotation ressents une force centrifuge, qui corresponds à l'opposé de l'accélération centripède dans le référentiel fixe.

conclusion

Ecrire vos conclusions dans la cellule suivante, en particulier sur l'équilibre de l'observateur lorsqu'il se penche vers l'axe de rotation ou vers vers l'extérieur.

Ecrire ici votre analyse et conclusion

FIN