Etude du mouvement gyroscopique

Mouvements de Lagrange d'une toupie

Marc BUFFAT département mécanique, université Lyon 1

%matplotlib inline
import numpy as np
import sympy as sp
import k3d
import matplotlib.pyplot as plt
from IPython.core.display import HTML
from IPython.display import display,Image
from sympy.physics.vector import init_vprinting
init_vprinting(use_latex='mathjax', pretty_print=False)

Documentation

• calcul symbolique Sympy: https://docs.sympy.org/latest/index.html

• bibliotheque Sympy de Mechanique classique: https://docs.sympy.org/latest/modules/physics/mechanics/index.html

• visualisation 3D k3d: https://k3d-jupyter.org/

Modélisation

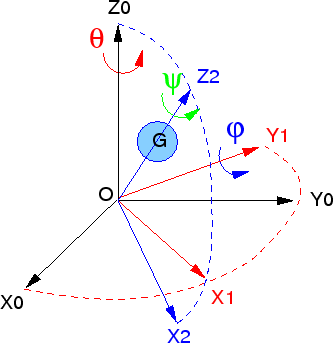
On modéliser la toupie comme une masse $m$ en $G$, distante de $l$ du point $O$, en rotation autour son axe principal d'inertie (axe de révolution) $\overrightarrow{OG}=l\,\overrightarrow{Z_{2}}$. On suppose que le point $O$ est immobile et la liaison sans frottement.

Les 3 degrés de liberté du système sont les 3 angles d'Euler:

1. $\theta$ l'angle de précession de l'axe de la toupie autour de $Z_{0}$

2. $\phi$ l'angle de nutation (oscillation de l'axe autour de $Y_{1}$)

3. $\psi$ l'angle de rotation propre de la toupie autour de son axe $Z_{2}$

Bilan des forces

La toupie est soumise aux forces suivantes:

1. la force de gravité $-mg\overrightarrow{Z_{0}}$ en $G$

2. la réaction $\overrightarrow{R}$ en $O$

L'application du théorème du moment cinétique en O permet d'obtenir les 3 équations du mouvement en $\theta$,$\phi$,$\psi$, en éliminant l'inconnue de tension (qui est obtenue par application du théorème sur la quantité de mouvement).

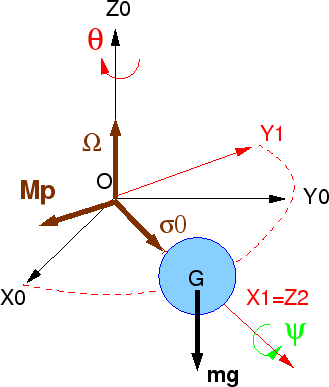
$$\frac{d}{dt}\overrightarrow{\sigma}(O)=-mgl\,\sin\phi\overrightarrow{Y_{1}}$$

Effet gyroscopique

Si à l'instant initial, la toupie tourne rapidement autour de son axe $Z_{2}$ avec une vitesse angulaire $\omega=\dot{\psi}$, le moment cinétique vaut approximativement

$$\overrightarrow{\sigma}(O)\approx I\omega\overrightarrow{Z_{2}}$$

(où $I$ est le moment d'inertie autour de l'axe $Z_{2}$). Le moment du poids engendre un couple suivant $\overrightarrow{Y_{1}}$ perpendiculaire à $\overrightarrow{\sigma}(O)$, qui force l'axe de rotation propre $Z_{2}$ à tourner autour d'un axe perpendiculaire à $Y_{1}$, $Z_{2}$ (effet gyroscopique). Si $\phi\approx\pi/2$ , alors la rotation s'effectue suivant $Z_{0}$ avec un mouvement lent de précession $\Omega=\dot{\theta}\approx cste$.

justification

En effet l'équation du mouvement (théorème du moment cinétique) s'écrit:

$$\frac{d}{dt}\overrightarrow{\sigma}(O)=\mathcal{M}_{O}(P)=l\overrightarrow{Z_{2}}\wedge-mg\overrightarrow{Z_{0}}$$

avec $\overrightarrow{\sigma}(O)\approx I\omega\overrightarrow{Z_{2}}$. D'où l'on déduit, si $\omega$ est très grand que:

$$\frac{d}{dt}\overrightarrow{\sigma}(O)=\Omega\overrightarrow{Z_{0}}\wedge\overrightarrow{\sigma}(O) \mbox{ avec } \Omega = -\frac{mgl}{I\omega} $$

Le moment cinétique $\overrightarrow{\sigma}(O)$, et donc la toupie se met à tourner autour de l'axe vertical $\overrightarrow{Z_{0}}$ avec une vitesse de rotation $\Omega$ (effet gyroscopique). Ce mouvement est appelé précession. La vitesse angulaire de la précession $\Omega$ est donnée par :

$$\Omega=-\frac{mgl}{I\omega}$$

et est d'autant plus petite que $\omega$ est grand.

La précession peut être démontrée en plaçant un gyroscope tournant sur son axe horizontal et supporté lâchement à une extrémité. Au lieu de tomber comme on peut s'y attendre, le gyroscope apparaît comme défiant la gravité en restant sur son axe horizontal, même si un bout de l'axe n'est pas supporté. L'extrémité libre de l'axe décrit lentement un cercle dans un plan horizontal. Le moment du gyroscope est fourni par un couple de forces : la gravité pousse vers le bas le centre de la masse du dispositif, et la réaction en O le pousse vers le haut pour supporter le côté libre. Le déplacement résultant de ce moment n'est pas vers le bas, comme l'intuition nous le fait supposer, mais perpendiculaire à la fois au mouvement gravitationnel (le bas) et l'axe de rotation (vers l'extérieur du point d'appui), c'est-à-dire dans une direction horizontale vers l'avant, faisant faire à l'appareil une rotation lente autour du point de support. La réaction en O possède donc une composante horizontale (et non pas uniquement vertical), qui génère ce déplacement .

La démonstration la plus simple et la plus parlante consiste à tenir à bout de bras une roue de vélo par les écrous du moyeu et de la faire tourner rapidement par une autre personne. Lorsque l'on tente de pencher sur le côté la roue en rotation, on verra que le mouvement sera décalé de 90° !

Etude du mouvement général

Dans le cas général, on a un mouvement beaucoup plus compliqué avec un mouvement de précession et de nutation de l'axe de la toupie, et des vitesses angulaires variants au cours du temps.

On note cependant que certaines quantités se conservent au cours du temps:

1. l'énergie totale = énergie cinétique + énergie potentielle: $$E=E_{c}+U=cste$$

2. la projection du moment cinétique suivant $\overrightarrow{Z_{2}}$ (passe par G) et suivant $\overrightarrow{Z_{0}}$ (direction du poids), puisque que le moment du poids est perpendiculaire à ces deux directions.

$$\overrightarrow{\sigma}(O).\overrightarrow{Z_{2}}=cste,\mbox{ et } \overrightarrow{\sigma}(O).\overrightarrow{Z_{0}}=cste$$

Ce sont les 3 intégrales premières du mouvement.

Modélisation

On définit 3 repères:

1. le repère fixe $\mathcal{R}_{0}(X_{0},Y_{0},Z_{0})$ avec $Z_{0}$ suivant la verticale

2. le repère $\mathcal{R}_{1}$ en rotation de $\theta$ (précession) autour de $Z_{0}$ avec $$\Omega_{1/0}=\Omega_{\mathcal{R}_{1}/\mathcal{R}_{0}}=\frac{d\theta}{dt}Z_{0}$$

3. le repère $\mathcal{R}_{2}$ en rotation de $\phi$ (nutation) autour de $Y_{1}$ avec $$\Omega_{2/1}=\Omega_{\mathcal{R}_{2}/\mathcal{R}_{1}}=\frac{d\phi}{dt}Y_{1}$$

4. la toupie est en rotation de $\psi$ (rotation propre) autour de son axe $$Z_{2}\Omega_{3/2}=\frac{d\psi}{dt}Z_{2}$$

Les matrices de changement de repère s'écrivent:

$$\mathcal{M}_{0/1}=\left[\begin{array}{ccc} \cos\theta & -\sin\theta & 0\\ \sin\theta & \cos\theta & 0\\ 0 & 0 & 1 \end{array}\right],\,\,\,\mathcal{M}_{1/0}=\mathcal{M}_{0/1}^{t}$$$$\mathcal{M}_{1/2}=\left[\begin{array}{ccc} \cos\phi & 0 & \sin\phi\\ 0 & 1 & 0\\ -\sin\phi & 0 & \cos\phi \end{array}\right],\,\,\,\mathcal{M}_{2/1}=\mathcal{M}_{1/2}^{t}$$

La toupie est un solide de révolution d'axe $Z_{2}$, donc dans $\mathcal{R}_{2}$ la matrice d'inertie est diagonale et vaut:

$$\mathcal{I}_{G}=\left[\begin{array}{ccc} I_{2} & 0 & 0\\ 0 & I_{2} & 0\\ 0 & 0 & I_{1} \end{array}\right]$$

Prise en compte du frottement

Pour prendre en compte le frottement de la toupie en O, on introduit un couple de frottement en O proportionnelle à la vitesse de rotation propre $\dot{\psi}$

$$ C_f = -I_1 K \dot{\psi} Z_2 $$

Modélisation sympy

from sympy.physics.mechanics import dynamicsymbols, Point, ReferenceFrame
from sympy.physics.mechanics import RigidBody
from sympy.physics.vector import dot

# parametres du problème
l, m, g, I1, I2, K = sp.symbols('l m g I_1 I_2 K')
# degrés de liberté
theta, phi, psi = dynamicsymbols('theta phi psi')
thetap, phip, psip = dynamicsymbols('theta phi psi',level=1)
thetap2, phip2, psip2 = dynamicsymbols('theta phi psi',level=2)
t = sp.symbols('t')

# reperes
O = Point('O')
R0 = ReferenceFrame('R_0')
R1 = ReferenceFrame('R_1')
R1.orient(R0,'Axis',[theta, R0.z])
R2 = ReferenceFrame('R_2')
R2.orient(R1,'Axis',[phi, R1.y])
R3 = ReferenceFrame('R_3')
R3.orient(R2,'Axis',[psi, R2.z])
G = Point('G')
G.set_pos(O,l*R2.z)

# vitesse angulaire de R3/R0
R3.ang_vel_in(R0)

$\displaystyle \dot{\psi}\mathbf{\hat{r_2}_z} + \dot{\phi}\mathbf{\hat{r_1}_y} + \dot{\theta}\mathbf{\hat{r_0}_z}$

# et acceleration
R3.ang_acc_in(R0)

$\displaystyle \dot{\phi} \dot{\psi}\mathbf{\hat{r_2}_x} + \operatorname{sin}\left(\phi\right) \dot{\psi} \dot{\theta}\mathbf{\hat{r_2}_y} + \ddot{\psi}\mathbf{\hat{r_2}_z} - \dot{\phi} \dot{\theta}\mathbf{\hat{r_1}_x} + \ddot{\phi}\mathbf{\hat{r_1}_y} + \ddot{\theta}\mathbf{\hat{r_0}_z}$

# matrice d'inertie
from sympy.physics.mechanics import inertia
IG = inertia(R2,I2,I2,I1)
IG

$\displaystyle I_{2}\mathbf{\hat{r_2}_x}\otimes \mathbf{\hat{r_2}_x} + I_{2}\mathbf{\hat{r_2}_y}\otimes \mathbf{\hat{r_2}_y} + I_{1}\mathbf{\hat{r_2}_z}\otimes \mathbf{\hat{r_2}_z}$

# O fixe dans R0 et G fixe dans R2 (et R3)
O.set_vel(R0,0.)
G.set_vel(R2,0.)

# Définition du solide toupie avec R3 repere lié à la toupie
toupie = RigidBody('Toupie',G,R3,m,(IG,G))

calcul des vitesses par composition des vitesses

O et G appartiennent au même solide et sont fixes dans $R_2$ $$ V_{G/R_0} = V_{O/R_0} + \Omega_{R_2/R_O} \wedge OG $$

# composition des vitesses: vitesse de G / R0
G.v2pt_theory(O,R0,R2)

$\displaystyle l \dot{\phi}\mathbf{\hat{r_2}_x} + l \operatorname{sin}\left(\phi\right) \dot{\theta}\mathbf{\hat{r_2}_y}$

# et son accélération / R0
G.acc(R0)

$\displaystyle (- l \operatorname{sin}\left(\phi\right) \operatorname{cos}\left(\phi\right) \dot{\theta}^{2} + l \ddot{\phi})\mathbf{\hat{r_2}_x} + (l \operatorname{sin}\left(\phi\right) \ddot{\theta} + 2 l \operatorname{cos}\left(\phi\right) \dot{\phi} \dot{\theta})\mathbf{\hat{r_2}_y} + (- l \operatorname{sin}^{2}\left(\phi\right) \dot{\theta}^{2} - l \dot{\phi}^{2})\mathbf{\hat{r_2}_z}$

# moment cinétique en G / R0
from sympy.physics.mechanics import linear_momentum, angular_momentum
angular_momentum(G,R0,toupie)

$\displaystyle - I_{2} \operatorname{sin}\left(\phi\right) \dot{\theta}\mathbf{\hat{r_2}_x} + I_{2} \dot{\phi}\mathbf{\hat{r_2}_y} + I_{1} \left(\operatorname{cos}\left(\phi\right) \dot{\theta} + \dot{\psi}\right)\mathbf{\hat{r_2}_z}$

# moment cinetique en O
sigma_O = angular_momentum(O,R0,toupie)
sigma_O

$\displaystyle (- I_{2} \operatorname{sin}\left(\phi\right) \dot{\theta} - l^{2} m \operatorname{sin}\left(\phi\right) \dot{\theta})\mathbf{\hat{r_2}_x} + (I_{2} \dot{\phi} + l^{2} m \dot{\phi})\mathbf{\hat{r_2}_y} + I_{1} \left(\operatorname{cos}\left(\phi\right) \dot{\theta} + \dot{\psi}\right)\mathbf{\hat{r_2}_z}$

# simplification I2O = I2 + ml^2
I2O = sp.symbols('I_2O')
sigma_O=sigma_O.subs(I2,I2O-m*l**2).simplify()

équations du mouvement: PFD

$$\frac{d}{dt}\overrightarrow{\sigma}(O)=\mathcal{M}_{O}(P)+ C_f$$

# derivation du moment cinétique / R0
from sympy.physics.vector import time_derivative,dot
sigma_Op = time_derivative(sigma_O,R0)
sigma_Op

$\displaystyle (I_{1} \left(\operatorname{cos}\left(\phi\right) \dot{\theta} + \dot{\psi}\right) \dot{\phi} - I_{2O} \operatorname{sin}\left(\phi\right) \ddot{\theta} - 2 I_{2O} \operatorname{cos}\left(\phi\right) \dot{\phi} \dot{\theta})\mathbf{\hat{r_2}_x} + (I_{1} \left(\operatorname{cos}\left(\phi\right) \dot{\theta} + \dot{\psi}\right) \operatorname{sin}\left(\phi\right) \dot{\theta} - I_{2O} \operatorname{sin}\left(\phi\right) \operatorname{cos}\left(\phi\right) \dot{\theta}^{2} + I_{2O} \ddot{\phi})\mathbf{\hat{r_2}_y} + I_{1} \left(- \operatorname{sin}\left(\phi\right) \dot{\phi} \dot{\theta} + \operatorname{cos}\left(\phi\right) \ddot{\theta} + \ddot{\psi}\right)\mathbf{\hat{r_2}_z}$

# vecteur poids
-m*g*R0.z
# moment du poids
Mp = G.pos_from(O)^(-m*g*R1.z)
Mp

$\displaystyle g l m \operatorname{sin}\left(\phi\right)\mathbf{\hat{r_1}_y}$

# dans R2
Mp = Mp.express(R2)
Mp

$\displaystyle g l m \operatorname{sin}\left(\phi\right)\mathbf{\hat{r_2}_y}$

# couple de frottement 
Cf = -K*I1*psip*R2.z
Cf

$\displaystyle - I_{1} K \dot{\psi}\mathbf{\hat{r_2}_z}$

# equations du mouvement
Eqs = sigma_Op - Mp -Cf
Eqs

$\displaystyle (I_{1} \left(\operatorname{cos}\left(\phi\right) \dot{\theta} + \dot{\psi}\right) \dot{\phi} - I_{2O} \operatorname{sin}\left(\phi\right) \ddot{\theta} - 2 I_{2O} \operatorname{cos}\left(\phi\right) \dot{\phi} \dot{\theta})\mathbf{\hat{r_2}_x} + (I_{1} \left(\operatorname{cos}\left(\phi\right) \dot{\theta} + \dot{\psi}\right) \operatorname{sin}\left(\phi\right) \dot{\theta} - I_{2O} \operatorname{sin}\left(\phi\right) \operatorname{cos}\left(\phi\right) \dot{\theta}^{2} + I_{2O} \ddot{\phi} - g l m \operatorname{sin}\left(\phi\right))\mathbf{\hat{r_2}_y} + (I_{1} K \dot{\psi} + I_{1} \left(- \operatorname{sin}\left(\phi\right) \dot{\phi} \dot{\theta} + \operatorname{cos}\left(\phi\right) \ddot{\theta} + \ddot{\psi}\right))\mathbf{\hat{r_2}_z}$

# équations projetés dans R2
display(sp.Eq(Eqs.dot(R2.x),0))
display(sp.Eq(Eqs.dot(R2.y),0))
display(sp.Eq(Eqs.dot(R2.z),0))

$\displaystyle I_{1} \left(\operatorname{cos}\left(\phi\right) \dot{\theta} + \dot{\psi}\right) \dot{\phi} - I_{2O} \operatorname{sin}\left(\phi\right) \ddot{\theta} - 2 I_{2O} \operatorname{cos}\left(\phi\right) \dot{\phi} \dot{\theta} = 0$

$\displaystyle I_{1} \left(\operatorname{cos}\left(\phi\right) \dot{\theta} + \dot{\psi}\right) \operatorname{sin}\left(\phi\right) \dot{\theta} - I_{2O} \operatorname{sin}\left(\phi\right) \operatorname{cos}\left(\phi\right) \dot{\theta}^{2} + I_{2O} \ddot{\phi} - g l m \operatorname{sin}\left(\phi\right) = 0$

$\displaystyle I_{1} K \dot{\psi} + I_{1} \left(- \operatorname{sin}\left(\phi\right) \dot{\phi} \dot{\theta} + \operatorname{cos}\left(\phi\right) \ddot{\theta} + \ddot{\psi}\right) = 0$

Intégrales premières

# energie cinétique
Ec = toupie.kinetic_energy(R0)
Ec = Ec.subs(I2,I2O-m*l**2).simplify()
Ec

$\displaystyle \frac{I_{1} \operatorname{cos}^{2}\left(\phi\right) \dot{\theta}^{2}}{2} + I_{1} \operatorname{cos}\left(\phi\right) \dot{\psi} \dot{\theta} + \frac{I_{1} \dot{\psi}^{2}}{2} + \frac{I_{2O} \operatorname{sin}^{2}\left(\phi\right) \dot{\theta}^{2}}{2} + \frac{I_{2O} \dot{\phi}^{2}}{2}$

# et potentielle
toupie.potential_energy = m*g*dot(G.pos_from(O),R0.z)
Ep = toupie.potential_energy
Ep

$\displaystyle g l m \operatorname{cos}\left(\phi\right)$

# conservation moment cinétique / R2.z
s2z = dot(sigma_O,R2.z)
s2z

$\displaystyle I_{1} \left(\operatorname{cos}\left(\phi\right) \dot{\theta} + \dot{\psi}\right)$

# conservation moment cinétique / R0.z
s0z = dot(sigma_O,R0.z)
s0z

$\displaystyle I_{1} \left(\operatorname{cos}\left(\phi\right) \dot{\theta} + \dot{\psi}\right) \operatorname{cos}\left(\phi\right) + I_{2O} \operatorname{sin}^{2}\left(\phi\right) \dot{\theta}$

# conservation energie totale
Et = Ep + Ec
Et = Et.collect(I1)
Et

$\displaystyle I_{1} \left(\frac{\operatorname{cos}^{2}\left(\phi\right) \dot{\theta}^{2}}{2} + \operatorname{cos}\left(\phi\right) \dot{\psi} \dot{\theta} + \frac{\dot{\psi}^{2}}{2}\right) + \frac{I_{2O} \operatorname{sin}^{2}\left(\phi\right) \dot{\theta}^{2}}{2} + \frac{I_{2O} \dot{\phi}^{2}}{2} + g l m \operatorname{cos}\left(\phi\right)$

simplification

# parametres
omega, cste = sp.symbols('omega cste')
display(sp.Eq(omega , s2z/I1))

$\displaystyle \omega = \operatorname{cos}\left(\phi\right) \dot{\theta} + \dot{\psi}$

# simplification omega**2/2
exp = (s2z**2/I1**2/2).expand()
exp

$\displaystyle \frac{\operatorname{cos}^{2}\left(\phi\right) \dot{\theta}^{2}}{2} + \operatorname{cos}\left(\phi\right) \dot{\psi} \dot{\theta} + \frac{\dot{\psi}^{2}}{2}$

intégrales premières simplifiées

sp.Eq(s2z/I1,omega)

$\displaystyle \operatorname{cos}\left(\phi\right) \dot{\theta} + \dot{\psi} = \omega$

s0z = s0z.subs(s2z/I1,omega).expand()
sp.Eq(s0z,cste)

$\displaystyle I_{1} \omega \operatorname{cos}\left(\phi\right) + I_{2O} \operatorname{sin}^{2}\left(\phi\right) \dot{\theta} = cste$

Et0 = Et.subs(exp,omega**2/2).collect(I2O) - I1*omega**2/2
sp.Eq(Et0,cste)

$\displaystyle I_{2O} \left(\frac{\operatorname{sin}^{2}\left(\phi\right) \dot{\theta}^{2}}{2} + \frac{\dot{\phi}^{2}}{2}\right) + g l m \operatorname{cos}\left(\phi\right) = cste$

Application

Cas d'une toupie = disque de rayon $R$ sur un axe $l = 2R$

R , alpha = sp.symbols('R alpha')
display(sp.Eq(alpha, g/R))
display(sp.Eq(I1,  m*R**2/2))
display(sp.Eq(I2O, m*R**2 + m*l**2).subs(l,2*R))
vals = [(I1,m*R**2/2),(I2,m*R**2),(I2O,5*m*R**2),(l,2*R)]
vals

$\displaystyle \alpha = \frac{g}{R}$

$\displaystyle I_{1} = \frac{R^{2} m}{2}$

$\displaystyle I_{2O} = 5 R^{2} m$

$\displaystyle \left[ \left( I_{1}, \ \frac{R^{2} m}{2}\right), \ \left( I_{2}, \ R^{2} m\right), \ \left( I_{2O}, \ 5 R^{2} m\right), \ \left( l, \ 2 R\right)\right]$

Intégrales premières du mouvement

eq1 = s2z/I1
sp.Eq(eq1,omega)

$\displaystyle \operatorname{cos}\left(\phi\right) \dot{\theta} + \dot{\psi} = \omega$

eq2=(s0z.subs(vals)/(m*R**2)).expand()
sp.Eq(eq2,cste)

$\displaystyle \frac{\omega \operatorname{cos}\left(\phi\right)}{2} + 5 \operatorname{sin}^{2}\left(\phi\right) \dot{\theta} = cste$

eq3=(Et0.subs(vals)/(m*R**2)).expand()
sp.Eq(eq3,cste)

$\displaystyle \frac{5 \operatorname{sin}^{2}\left(\phi\right) \dot{\theta}^{2}}{2} + \frac{5 \dot{\phi}^{2}}{2} + \frac{2 g \operatorname{cos}\left(\phi\right)}{R} = cste$

validation: cas d'un mouvement de précession

pour une rotation très rapide de la toupie avec un angle initiale $\phi = \frac{\pi}{2}$

on doit trouver: $$\dot{\psi} = cste$$ $$\dot{\theta} = cste$$

Vérification avec les intégrales premières

# condition 
val1 = [(phi,sp.pi/2)]
val1

$\displaystyle \left[ \left( \phi, \ \frac{\pi}{2}\right)\right]$

# vérification / liste des intégrales premières
display(sp.Eq(eq1.subs(val1),cste))
display(sp.Eq(eq2.subs(val1),cste))
display(sp.Eq(eq3.subs(val1).doit(),cste))

$\displaystyle \dot{\psi} = cste$

$\displaystyle 5 \dot{\theta} = cste$

$\displaystyle \frac{5 \dot{\theta}^{2}}{2} = cste$

Application numérique: cas sans frottement

Valsnum = [(l,2*R), (alpha,g/R),  (g,9.81), (R,0.1), (K,0)]
display(Valsnum)
display(vals)

$\displaystyle \left[ \left( l, \ 2 R\right), \ \left( \alpha, \ \frac{g}{R}\right), \ \left( g, \ 9.81\right), \ \left( R, \ 0.1\right), \ \left( K, \ 0\right)\right]$

$\displaystyle \left[ \left( I_{1}, \ \frac{R^{2} m}{2}\right), \ \left( I_{2}, \ R^{2} m\right), \ \left( I_{2O}, \ 5 R^{2} m\right), \ \left( l, \ 2 R\right)\right]$

calcul mouvement de la toupie par résolution des 3 EDO

eq1=sp.simplify(Eqs.subs(vals).dot(R2.x)/(R**2*m/2))
sp.Eq(eq1,0)

$\displaystyle - 10 \operatorname{sin}\left(\phi\right) \ddot{\theta} - 19 \operatorname{cos}\left(\phi\right) \dot{\phi} \dot{\theta} + \dot{\phi} \dot{\psi} = 0$

eq2=sp.simplify(Eqs.subs(vals).dot(R2.y)/(R**2*m/4)).subs(g,alpha*R)
sp.Eq(eq2,0)

$\displaystyle - 8 \alpha \operatorname{sin}\left(\phi\right) + 2 \operatorname{sin}\left(\phi\right) \dot{\psi} \dot{\theta} - 9 \operatorname{sin}\left(2 \phi\right) \dot{\theta}^{2} + 20 \ddot{\phi} = 0$

eq3=sp.simplify(Eqs.subs(vals).dot(R2.z)/(R**2*m/2))
sp.Eq(eq3,0)

$\displaystyle K \dot{\psi} - \operatorname{sin}\left(\phi\right) \dot{\phi} \dot{\theta} + \operatorname{cos}\left(\phi\right) \ddot{\theta} + \ddot{\psi} = 0$

changement de variables pour la résolution numérique

Pour résoudre numériquement le modèle, on transforme les 3 EDO du 2nd ordre (PFD) en un systèmes d'EDO du 1er ordre avec un changement de variables:

$$ Y = [\theta, \phi, \psi, \dot{\theta}, \dot{\phi}, \dot{\psi}] $$$$ dY = \dot{Y} = [\dot{\theta}, \dot{\phi}, \dot{\psi}, \ddot{\theta}, \ddot{\phi}, \ddot{\psi}] $$

Le système d'équations 6x6 s'écrit $$ G(Y,\dot{Y}) =0 $$ avec $$ dY[0] = \dot{Y}[0] \;,\; dY[1] = \dot{Y}[1] \;,\; dY[2] = \dot{Y}[2]$$ et les 3 équations du mouvement

Implémentation dans une classe Toupie qui à partir des équations du mouvement, fait le changement de variables et résoud le système d'EDO du 1er ordre avec la bibliothéque implicite SUNDIALS, et la visualisation 3D avec K3D.

calcul de la solution pour une CI donnée

def CI(cas=0):
    """choix de la conditions aux limites (intéressantes): renvoie Y0 et tmax"""
    if cas == 1:
        # mvt precession   
        return np.array([0.,np.pi/2,0.,1.,0.,400.]), 8 
    elif cas == 2:
        # petits festons
        return np.array([0.,np.pi/4,0.,1.,0.,200.]), 2
    elif cas == 3:
        return np.array([0.,np.pi/4,0.,4.,0.,100.]), 2
    elif cas == 4:
        # boucle arriere
        return np.array([0.,np.pi/4,0.,8.,0.,200.]), 4
    elif cas == 5:
        # pendule
        return np.array([0.,np.pi/2,0.,0.,0.,10.]), 6
    else:
        # grandes boucles
        return np.array([0.,np.pi/4,0.,-8.,8.,100.]), 2
        

from Toupie import Toupie
# choix de la CI 
Y0,tmax = CI(4)
print("CI=",Y0,"tmax=",tmax)
# parametres du problème: 6 ddl (V), 3 equations (EQS), coordonnées du centre de gavité (CG) et energie (EN)
V   = [theta,phi,psi,thetap,phip,psip]
EQS = [eq1.subs(Valsnum),eq2.subs(Valsnum),eq3.subs(Valsnum)]
CG  = [G.pos_from(O).dot(R0.x).subs(Valsnum),
       G.pos_from(O).dot(R0.y).subs(Valsnum),
       G.pos_from(O).dot(R0.z).subs(Valsnum)]
EN   = [sp.simplify(Ec.subs(vals)/m).subs(Valsnum),
       (Ep.subs(vals)/m).subs(Valsnum)]

T = Toupie(V,EQS,CG,EN)
# calcul de la solution numérique
T.solve(Y0,tmax)

CI= [  0.           0.78539816   0.           8.           0.
 200.        ] tmax= 4

# tracer de la solution angles et positions de G
plt.figure(figsize=(12,6))
plt.subplot(1,2,1)
plt.plot(T.t,T.THETAP,label="$\dot{\\theta}$")
plt.plot(T.t,T.PHIP,label="$\dot{\phi}$")
plt.plot(T.t,T.PSIP,label="$\dot{\psi}$")
plt.title('vitesse de rotation')
plt.legend()
plt.subplot(1,2,2)
plt.plot(T.t,T.XG,label="$x_G$")
plt.plot(T.t,T.YG,label="$y_G$")
plt.plot(T.t,T.ZG,label="$z_G$")
plt.title('position de G')
plt.legend();

# tracer de l'énergie du système
plt.plot(T.t,T.EC-T.EC[0],label="Ec")
plt.plot(T.t,T.EP-T.EP[0],label="Ep")
plt.plot(T.t,T.EC+T.EP-T.EC[0]-T.EP[0],label="Et")
plt.title("énergie cinétique, potentielle et totale / a $t=0$")
plt.legend();

tracé du mouvement en 3D

Cas d'une solution avec des festons et une toupie qui retourne en arrière en décrivant des boucles sans tomber.

print("Mouvement toupie: cas sans frottement")
T.trace()

Mouvement toupie: cas sans frottement

T.trajectoire()

images et animation de la solution

position initiale	position finale

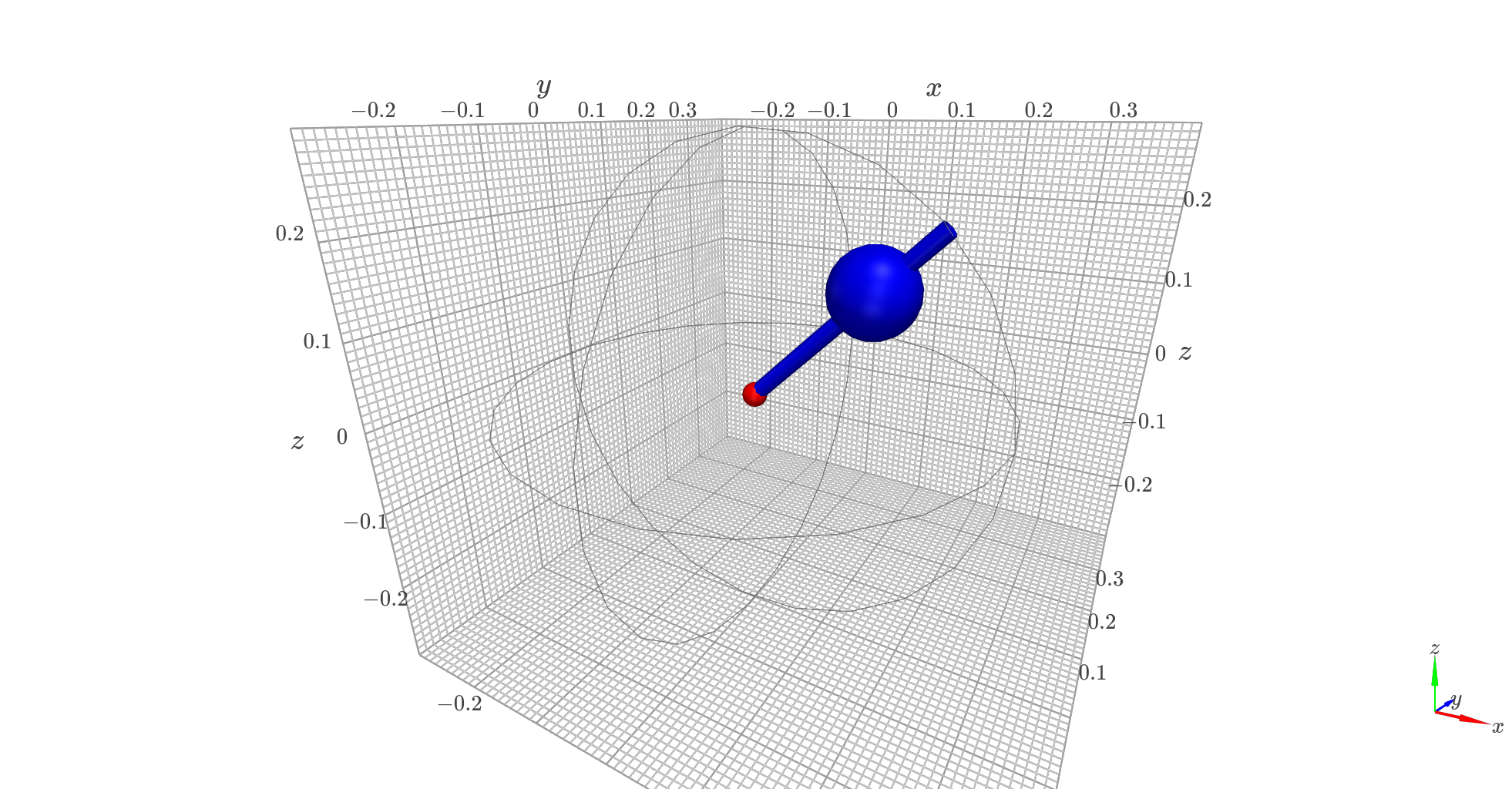animation de la solution

Analyse du mouvement de précession (sans frottement)

 calcul de la réaction $R_O$ en O par application du PFD

$$ m \frac{dV_G}{dt} -P = R_O $$

Valsnum = [(l,2*R), (alpha,g/R),  (g,9.81), (R,0.1), (K,0), (m,0.2)]
display(Valsnum)
display(vals)

$\displaystyle \left[ \left( l, \ 2 R\right), \ \left( \alpha, \ \frac{g}{R}\right), \ \left( g, \ 9.81\right), \ \left( R, \ 0.1\right), \ \left( K, \ 0\right), \ \left( m, \ 0.2\right)\right]$

$\displaystyle \left[ \left( I_{1}, \ \frac{R^{2} m}{2}\right), \ \left( I_{2}, \ R^{2} m\right), \ \left( I_{2O}, \ 5 R^{2} m\right), \ \left( l, \ 2 R\right)\right]$

R_O=time_derivative(linear_momentum(R0,toupie),R0)+m*g*R0.z
display(R_O)

$\displaystyle (- l m \operatorname{sin}\left(\phi\right) \operatorname{cos}\left(\phi\right) \dot{\theta}^{2} + l m \ddot{\phi})\mathbf{\hat{r_2}_x} + (l m \operatorname{sin}\left(\phi\right) \ddot{\theta} + 2 l m \operatorname{cos}\left(\phi\right) \dot{\phi} \dot{\theta})\mathbf{\hat{r_2}_y} + (- l m \operatorname{sin}^{2}\left(\phi\right) \dot{\theta}^{2} - l m \dot{\phi}^{2})\mathbf{\hat{r_2}_z} + g m\mathbf{\hat{r_0}_z}$

résolution numérique du mouvement

eq1=sp.simplify(Eqs.subs(vals).dot(R2.x)/(R**2*m/2))
display(eq1)
eq2=sp.simplify(Eqs.subs(vals).dot(R2.y)/(R**2*m/4)).subs(g,alpha*R)
display(eq2)
eq3=sp.simplify(Eqs.subs(vals).dot(R2.z)/(R**2*m/2))
display(eq3)

$\displaystyle - 10 \operatorname{sin}\left(\phi\right) \ddot{\theta} - 19 \operatorname{cos}\left(\phi\right) \dot{\phi} \dot{\theta} + \dot{\phi} \dot{\psi}$

$\displaystyle - 8 \alpha \operatorname{sin}\left(\phi\right) + 2 \operatorname{sin}\left(\phi\right) \dot{\psi} \dot{\theta} - 9 \operatorname{sin}\left(2 \phi\right) \dot{\theta}^{2} + 20 \ddot{\phi}$

$\displaystyle K \dot{\psi} - \operatorname{sin}\left(\phi\right) \dot{\phi} \dot{\theta} + \operatorname{cos}\left(\phi\right) \ddot{\theta} + \ddot{\psi}$

from Toupie import Toupie
# CI 
Y0,tmax = CI(1)
Y0[-1]=400
display(Y0)
#
V   = [theta,phi,psi,thetap,phip,psip]
EQS = [eq1.subs(Valsnum),eq2.subs(Valsnum),eq3.subs(Valsnum)]
CG  = [G.pos_from(O).dot(R0.x).subs(Valsnum),
       G.pos_from(O).dot(R0.y).subs(Valsnum),
       G.pos_from(O).dot(R0.z).subs(Valsnum)]
EN   = [sp.simplify(Ec.subs(vals)/m).subs(Valsnum),
       (Ep.subs(vals)/m).subs(Valsnum)]

T = Toupie(V,EQS,CG,EN)
# calcul solution numérique
T.solve(Y0,tmax)

array([  0.        ,   1.57079633,   0.        ,   1.        ,
         0.        , 400.        ])

# tracer de la solution angles et positions de G
plt.figure(figsize=(12,6))
plt.subplot(1,2,1)
plt.plot(T.t,T.THETAP,label="$\dot{\\theta}$")
plt.plot(T.t,T.PHIP,label="$\dot{\phi}$")
plt.plot(T.t,T.PSIP,label="$\dot{\psi}$")
plt.title('vitesse de rotation')
plt.legend()
plt.subplot(1,2,2)
plt.plot(T.t,T.XG,label="$x_G$")
plt.plot(T.t,T.YG,label="$y_G$")
plt.plot(T.t,T.ZG,label="$z_G$")
plt.title('position de G')
plt.legend();

calcul de la réaction

on a donc : $$\phi = \frac{\pi}{2}, \dot{\theta} = cste , \dot{\psi} = cste \gg \dot{\theta}, \dot{\phi} \approx 0 $$

# solution approchée
vals2 = [(thetap.diff(),0),(phip.diff(),0),
         (thetap, Y0[3]),(phip,Y0[4]),(psip,Y0[5]),
         (theta,Y0[0]+Y0[3]*t),(phi,Y0[1]+Y0[4]*t),(psi,Y0[2]+Y0[5]*t)]
vals2

$\displaystyle \left[ \left( \ddot{\theta}, \ 0\right), \ \left( \ddot{\phi}, \ 0\right), \ \left( \dot{\theta}, \ 1.0\right), \ \left( \dot{\phi}, \ 0.0\right), \ \left( \dot{\psi}, \ 400.0\right), \ \left( \theta, \ 1.0 t\right), \ \left( \phi, \ 1.5707963267949\right), \ \left( \psi, \ 400.0 t\right)\right]$

# composantes de R_O dans R0
R_Ox=R_O.dot(R0.x).subs(Valsnum).subs(vals2)
display(R_Ox)
R_Oy=R_O.dot(R0.y).subs(Valsnum).subs(vals2)
display(R_Oy)
R_Oz=R_O.dot(R0.z).subs(Valsnum).subs(vals2)
display(R_Oz)
poids = -(m*g).subs(Valsnum)
print("mg=",poids)

$\displaystyle - 0.04 \operatorname{cos}\left(1.0 t\right)$

$\displaystyle - 0.04 \operatorname{sin}\left(1.0 t\right)$

$\displaystyle 1.962$

mg= -1.96200000000000

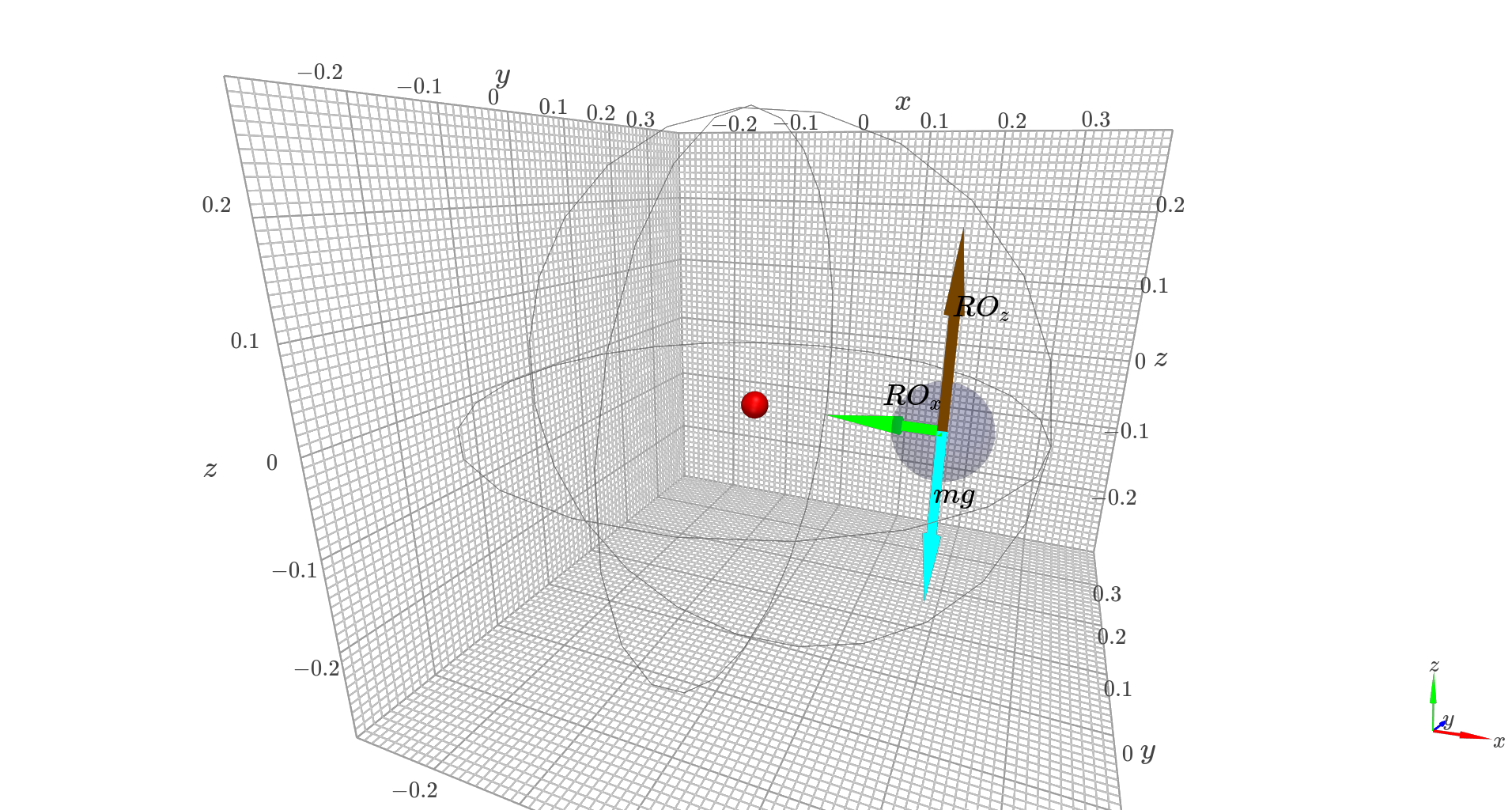
La réaction a donc une composante verticale qui compense exactement le poids et une compoante suivant l'axe de la toupie $R2.z$, qui correspond à l'accélération centrifuge associée au mouvement de précéssion

Gpt = np.array([T.XG[0],T.YG[0],T.ZG[0]]).astype(np.float32)
RR  = 3*np.array([R_Ox.subs(t,0),R_Oy.subs(t,0),0.0]).astype(np.float32)
PP  = 0.1*np.array([0,0,poids]).astype(np.float32)
print("Bilan des forces sur la toupie")
T.trace()
T.Tige.visible=False
T.Masse.opacity=0.3
T.plot += k3d.factory.vectors(Gpt,RR,color=0x00ff00,line_width=0.01,shader='mesh', head_size=0.4,labels=[" RO_x"])
T.plot += k3d.factory.vectors(Gpt,PP,color=0x00ffff,line_width=0.01,shader='mesh', head_size=0.4,labels=[" mg"])
T.plot += k3d.factory.vectors(Gpt,-PP,color=0x774400,line_width=0.01,shader='mesh', head_size=0.4,labels=[" RO_z"])

Bilan des forces sur la toupie

visualisation des forces en G

Simulation du cas avec frottement $K\neq 0$

Valsnum = [(l,2*R), (alpha,g/R),  (g,9.81), (R,0.1), (K,0.8)]
display(Valsnum)
display(vals)

$\displaystyle \left[ \left( l, \ 2 R\right), \ \left( \alpha, \ \frac{g}{R}\right), \ \left( g, \ 9.81\right), \ \left( R, \ 0.1\right), \ \left( K, \ 0.8\right)\right]$

$\displaystyle \left[ \left( I_{1}, \ \frac{R^{2} m}{2}\right), \ \left( I_{2}, \ R^{2} m\right), \ \left( I_{2O}, \ 5 R^{2} m\right), \ \left( l, \ 2 R\right)\right]$

eq1=sp.simplify(Eqs.subs(vals).dot(R2.x)/(R**2*m/2))
display(eq1)
eq2=sp.simplify(Eqs.subs(vals).dot(R2.y)/(R**2*m/4)).subs(g,alpha*R)
display(eq2)
eq3=sp.simplify(Eqs.subs(vals).dot(R2.z)/(R**2*m/2))
display(eq3)

$\displaystyle - 10 \operatorname{sin}\left(\phi\right) \ddot{\theta} - 19 \operatorname{cos}\left(\phi\right) \dot{\phi} \dot{\theta} + \dot{\phi} \dot{\psi}$

$\displaystyle - 8 \alpha \operatorname{sin}\left(\phi\right) + 2 \operatorname{sin}\left(\phi\right) \dot{\psi} \dot{\theta} - 9 \operatorname{sin}\left(2 \phi\right) \dot{\theta}^{2} + 20 \ddot{\phi}$

$\displaystyle K \dot{\psi} - \operatorname{sin}\left(\phi\right) \dot{\phi} \dot{\theta} + \operatorname{cos}\left(\phi\right) \ddot{\theta} + \ddot{\psi}$

from Toupie import Toupie
# CI 
Y0,tmax = CI(1)
display(Y0)
#
V   = [theta,phi,psi,thetap,phip,psip]
EQS = [eq1.subs(Valsnum),eq2.subs(Valsnum),eq3.subs(Valsnum)]
CG  = [G.pos_from(O).dot(R0.x).subs(Valsnum),
       G.pos_from(O).dot(R0.y).subs(Valsnum),
       G.pos_from(O).dot(R0.z).subs(Valsnum)]
EN   = [sp.simplify(Ec.subs(vals)/m).subs(Valsnum),
       (Ep.subs(vals)/m).subs(Valsnum)]

T = Toupie(V,EQS,CG,EN)
# calcul solution numérique
T.solve(Y0,tmax,Np=400)

array([  0.        ,   1.57079633,   0.        ,   1.        ,
         0.        , 400.        ])

# tracer de la solution angles et positions de G
plt.figure(figsize=(12,6))
plt.subplot(1,2,1)
plt.plot(T.t,T.THETAP,label="$\dot{\\theta}$")
plt.plot(T.t,T.PHIP,label="$\dot{\phi}$")
plt.plot(T.t,T.PSIP,label="$\dot{\psi}$")
plt.title('vitesse de rotation')
plt.legend()
plt.subplot(1,2,2)
plt.plot(T.t,T.XG,label="$x_G$")
plt.plot(T.t,T.YG,label="$y_G$")
plt.plot(T.t,T.ZG,label="$z_G$")
plt.title('position de G')
plt.legend();

# tracer de l'énergie du système
plt.plot(T.t,T.EC,label="Ec")
plt.plot(T.t,T.EP,label="Ep")
plt.plot(T.t,T.EC+T.EP,label="Et")
plt.title("énergie cinétique, potentielle et totale")
plt.legend();

visualisation 3D du mouvement

la toupie commence avec un mouvement de précession, mais la décroissance de sa rotation propre entraine sa chute, et elle termine avec un mouvement de pendule en rotation (pendule de Tournesol)

print("Cas avec frottement: la toupie tombe")
T.trace()

Cas avec frottement: la toupie tombe

T.trajectoire()

images et animation de la solution avec frottement

position initiale	position finale

animation de la solution avec frottement

FIN