4.2 Un exemple sous Maple

On étudie la cinématique d'une porte de placard KZ avec Maple. On détermine en particulier le centre instantanée de rotation.

4.2.1 Définition du problème

Soit une porte de placard, de type KZ, dont la coupe horizontale est donnée sur la figure suivante:

Il s'agit de deux portes de largeur $L$, dont la première $OA$ est en rotation autour de $O$ et la seconde $AB$ est telle que $B$ se déplace le long de l'axe $Ox$.

Le mouvement de ce système est paramétré par l'angle $\theta(t)$.

Pour étudier le mouvement d'un point $P$ de la porte $AB$, on écrit simplement les relations vectorielles:

$$\overrightarrow{OP}=\overrightarrow{OA}+x\overrightarrow{AB}$$

où $x$ est la position de $P$ sur $AB$.

On peut ainsi tracer les trajectoires de différents points $P$: trajectoires qui varient de la droite (cas $P=B$) à l'arc de cercle (cas $P=A$).

Pour analyser le mouvement de la porte $AB$, on détermine son centre instantané de rotation $I$.

Pour cela on calcule la vitesse des deux points $A$ et $B$, et on utilise la composition des vitesses pour déterminer le vecteur instantané de rotation $\overrightarrow{\Omega}$:

$$\overrightarrow{V}_{A}=\frac{d\overrightarrow{OA}}{dt}\,,\,\... ...htarrow{V}_{A}+\overrightarrow{\Omega}\wedge\overrightarrow{AB}$$

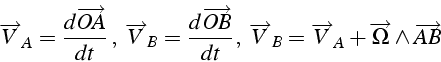
Le mouvement étant plan, $\overrightarrow{\Omega}$ a uniquement une composante $\omega(t)$ suivant $Oz$ , que l'on déduit des relations précédentes.

Ayant $\overrightarrow{\Omega}$, on en déduit le centre instantané de rotation en déterminant le point $M(X,Y)$ lié à $AB$ tel $\overrightarrow{V}_{M}=\overrightarrow{0}$ avec

$$\overrightarrow{V}_{M}=\overrightarrow{V}_{B}+\overrightarro... ...}}\,\overrightarrow{BM}=\overrightarrow{OM}-\overrightarrow{OB}$$

Au cours du temps, ce point $M$ varie par rapport à $AB$, i.e. le mouvement de $AB$ n'est pas un mouvement de rotation autour d'un point fixe.

On peut tracer la position de $I$ au cours du mouvement.

4.2.2 Solution avec Maple

Cinématique d'une porte KZ(version avec Maple)

Cinématique d'une porte KZ (version HTML)