3.3 Éléments finis $\mathcal{P}^{2}$

L'approximation par éléments finis $\mathcal{P}^{2}$ consiste à utiliser une interpolation polynomiale de degré 2 sur l'élèment de référence $\hat{e}$. On utilise les 3 points d'interpolations $\hat{S}_{1}$ $(\xi=-1)$, $\hat{S}_{2}$ $(\xi=1)$, $\hat{S}_{3}$ $(\xi=0)$ sur $\hat{e}$ associés à 3 points sur l'élément $e_{k}$ : les 2 extrémités du segment $S_{1}$, $S_{2}$ , et le milieu du segment $S_{3}$. On notera $\{ n_{1},n_{2},n_{3}\}$ les numéros de ces 3 noeuds (figure 4.17).

Figure: éléments finis $\mathcal{P}^{2}$

Sur l'élément de référence, on définit donc 3 fonctions de formes:

$$N_{1}(\xi)=\frac{\xi(\xi-1)}{2}, N_{2}(\xi)=\frac{\xi(\xi+1)}{2}, N_{3}(\xi)=1-\xi^{2}$$

qui sont tracées sur la figure ci dessous (figure 4.18).

Figure: Fonctions de forme $\mathcal{P}^{2}$ : $N_{1}$(rouge), $N_{2}$ (vert), $N_{3}$ (bleu)

3.3.1 Interpolation $\mathcal{P}^{2}$

Une approximation par éléments finis $\mathcal{P}^{2}$ sur un maillage de $ne$ éléments nécéssite $2ne+1=nn$ points nodaux: les $ne+1$ extrémités de segment et les $ne$ milieux. On numérote ces points de 1 à $nn$, et donc un élément $e_{k}$ a pour extrémités les sommets $S_{1}$ et $S_{2}$ de numéro $n_{1}=2k-1$ et $n_{2}=2k+1$, et pour noeud milieu le sommet $S_{3}$ de numéro $n_{3}=2k$. Les 3 fonctions de base $\{\Phi_{n_{q}}(x)\}_{q=1,3}$ associées à ces 3 sommets de numéro $\{ n_{q}\}_{q=1,3}$ sont définies en fonction des fonctions de formes $N_{q}(\xi)$ à l'aide de la transformation vers l'élèment de référence (figure 4.19).

Figure: élément $\mathcal{P}^{2}$

L'approximation $f^{h}$ par éléments $\mathcal{P}^{2}$ d'ne fonction $f(x)$ s'écrit globalement:

$$f^{h}(x)=\sum_{i=1}^{nn}f_{i}\Phi_{i}(x)$$

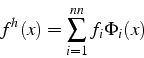
et sur chaque élément $e_{k}$ de sommets $(n_{1},n_{2},n_{3})$ du maillage:

$$f^{h}(x)=f_{n_{1}}\Phi_{n_{1}}(x)+f_{n_{2}}\Phi_{n_{2}}(x)+f_{n_{3}}\Phi_{n_{3}}(x)$$

où les fonctions de base $\Phi_{n_{q}}(x)$ sont définies à partir des fonctions de forme $N_{q}(\xi)$ par transformation vers l'élément de référence $\hat{e}$ :

$$\Phi_{n_{1}}(x)=N_{1}(\xi), \Phi_{n_{2}}(x)=N_{2}(\xi), \Phi_{n_{3}}(x)=N_{3}(\xi)$$

Le programme Maple 4.3.1 ci dessous implémente cette interpolation $\mathcal{P}^{2}$ .

programme Maple 4.3.1: Approximation par éléments finis P2

> restart:
# Approximation par elements finis 1D P2
> with(linalg): with(plots):
# Nombre d'éléments Ne et degre d'approximation par element k
> L:=3; Ne:=4;
# Maillage et coordonnes des pts de maillages
> h:=L/Ne; Xp:=[seq(i*h,i=0..Ne)];
# d=degre d'interpolation elts finis, Nn=Nombre de noeuds, X=coordonnees
# des nds 
> d:=2; Nn:=2*Ne+1;X:=vector(Nn,0):
> for i from 1 to Ne do X[2*i-1]:=Xp[i];X[2*i]:=(Xp[i]+Xp[i+1])/2; end:
> X[Nn]:=Xp[Ne+1]:
> evalm(X);
# num=numérotation par élément et long=longueur de chaque element
> num:=k->[2*k-1,2*k+1,2*k]; long:=k->Xp[k+1]-Xp[k];
# Fonctions de forme de l'element P2
> N1:=unapply(interp([-1,0,1],[1,0,0],xi),xi);
> N2:=unapply(interp([-1,0,1],[0,0,1],xi),xi);
> N3:=unapply(interp([-1,0,1],[0,1,0],xi),xi);
# Transformation vers l'element de reference [-1,1]
> Xi:=(xi,k)->(1-xi)/2*Xp[k]+(1+xi)/2*Xp[k+1];
# Interpolation d'une fonction g(x) sur le maillage
> Interpol:=proc(g)
> global Nn:
> local G,i;
> G:=vector(Nn,0):
> for i from 1 to Nn do G[i]:=g(X[i]); end;
> return evalm(G);
> end proc:
# Calcul de la norme L2 de l'erreur
> Erreur:=proc(f,F)
> global Ne,Xp;
> local err,k,noi,h;
> err:=0.0:
> for k from 1 to Ne do
>  h:=long(k):
>  noi:=num(k):
>  err:=err+h/2*
>  evalf(int((f(Xi(xi,k))-(F[noi[1]]*N1(xi)+F[noi[2]]*N2(xi)+
>      F[noi[3]]*N3(xi) ))^2,xi=-1..1));
> end:
> return(sqrt(err));
> end:
# Example: fonction cos(2x)
> f:=x->cos(2*x);
> F:=evalf(Interpol(f));
> P1:=plot(f(x),x=0..L):
> P2:=plot([seq([X[i],F[i]],i=1..Nn)],style=point,color=blue):
> display(P1,P2,title="Approximation P2 de cos(2x)");
> err:=Erreur(f,F);

Dans ce programme, les $ne+1$ points du maillage (extrémités des segments) sont notés Xp, alors que les $2ne+1$ points nodaux (i.e. degré de liberté) sont notés X et sont calculés en fonction de Xp (ligne 11). La numérotation des 3 points d'interpolation pour un élément k est donnée par la fonction num (ligne 15). Les 3 fonctions de forme sont calculées comme polynômes de Lagrange (lignes 17,18,19). Le changement de variable vers l'élément de référence est définie à la ligne 21, et la fonction d'interpolation à la ligne 23 (ce sont les mêmes que pour l'interpolation $\mathcal{P}^{1})$. Par contre le calcul de l'erreur moyenne d'interpolation (ligne 31) est différente de la fonction $\mathcal{P}^{1}$, puisque l'on fait explicitement intervenir les fonctions de forme par élément.

Figure: Fonctions de base et interpolation $\mathcal{P}^{2}$ sur un maillage $ne=4$

Les fonctions de base pour un maillage avec $ne=4$ éléments (et donc le même nombre de degré de liberté $nn=9$ que dans l'example du paragraphe 3.2.2 avec des éléments $\mathcal{P}^{1}$ ) sont tracées sur la figure (4.20) , ainsi que l'interpolation $\mathcal{P}^{2}$ de la fonction $f(x)=cos(2x)$ , que l'on comparera avec l'interpolation $\mathcal{P}^{1}$ de la figure (4.13) sur un maillage identique. On constate que l'approximation $\mathcal{P}^{2}$ est meilleure que l'approximation $\mathcal{P}^{1}$, ce qui est confirmée par la valeur de l'erreur moyenne: $\Vert f-f^{h}\Vert=0.024$ (soit plus de 2,5 fois plus faible).

3.3.2 Approximation par éléments finis $\mathcal{P}^{2}$

En suivant l'approche générale précédente, l'approximation $\mathcal{P}^{2}$ de la solution $u(x)$ du problème (4.20) s'écrit:

$$u^{h}(x)=\sum_{i=1}^{nn}u_{i}\Phi_{i}(x)$$

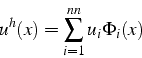
Elle vérifie la formulation faible discrète (4.23), qui est équivalente à un système linéaire de dimension $nn$:

$$\mathbf{A}[u_{j}]=\mathbf{B}$$

L'expression des coefficients de A et B est la même que dans la relation (4.23), mais les fonctions $\Phi _{i}$ sont maintenant les fonctions de base $\mathcal{P}^{2}$ définies précédemment. Comme avec les éléments finis $\mathcal{P}^{1}$ du paragrape 4.2, nous construirons tout d'abord la matrice A et le second membre B sans tenir compte des conditions aux limites, en calculant des matrices et des seconds membres élémentaires, puis nous appliquerons les conditions aux limites.

3.3.2.1 Matrices élémentaires

Les matrices élémentaires de raideur $\mathbf{K}^{k}$ et de masse $\mathbf{M}^{k}$ pour un élément $e_{k}$ sont données par les relations (4.24) et (4.25) avec $d=2$. Ce sont des matrices $3*3$ dont le calcul général est éffectué par les 2 fonctions Maple MatRigidite (programme 4.2.4) et MatMasse (programme 4.2.4).

Dans le cas où le coefficient $K(x)$ est constant par élément, la matrice élémentaire de raideur $\mathcal{P}^{2}$ s'écrit:

$$\mathbf{K}^{k}=K\frac{2}{h_{k}}\left[\begin{array}{ccc} +\fr... ...\ -\frac{4}{3} & -\frac{4}{3} & +\frac{8}{3}\end{array}\right]$$

De même si le coefficient $\alpha(x)$ est constant par élément, la matrice élémentaire de masse $\mathcal{P}^{2}$ s'écrit:

$$\mathbf{M}^{k}=\alpha\frac{h_{k}}{2}\left[\begin{array}{ccc}... ...\frac{2}{15} & +\frac{2}{15} & +\frac{16}{15}\end{array}\right]$$

Exercice: démontrer les deux résultats précédents.

3.3.2.2 Second membre élémentaire

Le second membre élémentaire pour un élément $e_{k}$ est donné par la relation générale (4.26) avec $d=2$. Pour le calcul on utilise la fonction Maple SmbElem (programme 4.2.5). L'expression obtenue pour ce second membre élémentaire en $\mathcal{P}^{2}$ s'écrit:

$$\mathbf{B}^{k}=\frac{h_{k}}{2}\left[\begin{array}{c} \frac{4... ... \frac{2f_{n_{1}}2f_{n_{2}}+16f_{n_{3}}}{15}\end{array}\right]$$

Exercice: démontrer cette relation.

3.3.2.3 Assemblage

La procédure d'assemblage reprend l'algorithme général (4.2.6). Ainsi pour le maillage de $ne=4$ éléments et $nn=9$ noeuds de la figure 4.21, la matrice élémentaire $\mathbf{A}^{2}$ de l'élémentaire $e_{2}$ contribue aux éléments suivants de la matrice A :

$$\begin{eqnarray*} A_{3,3}\leftarrow A_{3,3}+A_{1,1}^{2} & A_{3,5}\leftarrow A_{3... ...arrow A_{5,3}+A_{2,1}^{2} & A_{5,4}\leftarrow A_{5,4}+A_{2,3}^{2}\end{eqnarray*}$$

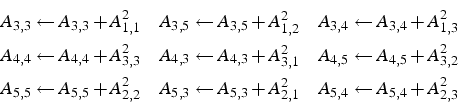
On notera que la numérotation des noeuds sur l'élément $e_{2}$ est dans l'ordre $3,4,5$ alors que sur l'élément de référence la numérotation est $1,3,2$ (on numérote d'abord les extrémités puis le milieu). On a a donc $n_{1}=3$, $n_{2}=5$ et $n_{3}=4$.

Figure: maillage $\mathcal{P}^{2}$ et transformation $\mathcal{T}_{2}:x=\frac{1-\xi}{2}x_{3}+\frac{1+\xi}{2}x_{5}$

3.3.2.4 Conditions aux limites

Les conditions aux limites sont imposées de la même façon qu'au paragraphe 4.2.7, et on utilise le programe Maple (programme 4.2.7).

En utilisant ces programmes Maple avec $d=2$, sur le maillage de la figure (4.21) qui contient $ne=4$ éléments (soit $nn=9$ inconnues), on obtiens la matrice $\mathbf{A}$ suivante:

$$\mathbf{A}=\left[\begin{array}{ccccccccc} 1.0 & 0.0 & 0.0 & ... ...0.0 & 0.0 & 0.0 & 0.0 & 83.0 & -669.0 & 590.0\end{array}\right]$$

et un second membre $\mathbf{B}$ :

$$\mathbf{B}=[60.0,314.0,157.0,314.0,157.0,314.0,157.0,314.0,46.5]$$

La solution obtenue vaut:

$$\mathbf{X}=[60.0,55.3,51.4,48.2,45.7,43.8,42.4,41.6,41.3]$$

Les valeurs nodales de la solution sont très proche de la solution exacte, ce que confirme le calcule de l'erreur moyenne qui est encore plus faible qu'avec l'approximation $\mathcal{P}^{1}$ ( $0.0054$ au lieu de $0.083$). Mais la grande différence avec l'approximation $\mathcal{P}^{1}$ se trouve sur le calcul du flux en $x=L$ : on trouve un flux égale à $30.16$ (au lieu de $158$ en $\mathcal{P}^{1}$), très proche de la valeur exacte $32$. Dans ce cas l'approximation $\mathcal{P}^{2}$ apporte une meilleure précision sur la dérivée en $x=L$, que l'approximation $\mathcal{P}^{1}$.

3.3.3 Etude de la précision

Pour quantifier cette étude, nous avons tracé l'erreur relative moyenne $\frac{\vert\vert u-u^{h}\vert\vert}{\vert\vert u\vert\vert}$ et l'erreur relative sur la condition aux limites en $x=L$ en fonction du nombre d'éléments $ne$ du maillage. Les résultats sont tracés en échelle logarithmique sur la figure (4.22) que l'on comparera avec la figure(4.16). On constate que l'erreur relative moyenne varie en $\frac{1}{ne^{3}}$ (soit en $\theta(h^{3})$) (comparaison avec une droite de pente $-3$), et que l'erreur relative sur la condition aux limites varie en $\frac{1}{ne^{3}}$ (soit aussi en $\theta(h^{3})$) . La précision de l'approximation $\mathcal{P}^{2}$ est donc d'ordre 3, i.e. en $\theta(h^{3})$, alors que la précision de l'approximation $\mathcal{P}^{1}$ est d'ordre 2, i.e. en $\theta(h^{2})$ (on a noté $h$ la taille caractéristique des éléments $h=\frac{L}{Ne}$)

Figure 4.22: Erreur relative en fonction de Ne (elt P2)

Exercice: modifier le programme Maple précédent pour faire l'étude avec des éléments $\mathcal{P}^{3}$. Montrez que dans ce cas la précision de l'approximation est d'ordre 4, i.e. en $\theta(h^{4})$.