suivant: 3.3 Éléments finis monter: 3. Méthode des éléments précédent: 3.1 Première approche Table des matières
Nous allons maintenant étudier l'approximation par éléments finis
![]() , en particulier ses propriétés en terme de précision
et de convergence. Nous donnerons en même temps le programme Maple
correspondant.
, en particulier ses propriétés en terme de précision
et de convergence. Nous donnerons en même temps le programme Maple
correspondant.
Pour cela nous allons traiter le cas d'une équation générale du type
(4.1) sur le domaine ![]() :
:
Cette équation traduit un phénomène de diffusion avec un coefficient
de diffusion ![]() variable, couplé à un terme source fonction de
la solution
variable, couplé à un terme source fonction de
la solution ![]() et d'un coefficient
et d'un coefficient ![]() variable. Le second
membre
variable. Le second
membre ![]() traduit la partie du terme source indépendant de
traduit la partie du terme source indépendant de ![]() .
En
.
En ![]() , on impose une condition de Dirichlet, et en
, on impose une condition de Dirichlet, et en ![]() une
condition de Fourier (ou condition de Robin, ou condition mixte) qui
impose que le flux de chaleur
une
condition de Fourier (ou condition de Robin, ou condition mixte) qui
impose que le flux de chaleur ![]() en
en ![]() soit une fonction
de la solution
soit une fonction
de la solution ![]() (et non pas uniquement constant comme dans
l'exemple précédent):
(et non pas uniquement constant comme dans
l'exemple précédent):
![]()
Pour obtenir la formulation faible de (4.19), on procède comme
précédemment. On multiplie l'équation (4.19) par une fonction
test ![]() , on intègre sur le domaine
, on intègre sur le domaine ![]() , puis on effectue
une intégration par partie sur les termes de plus haut degré. Il vient:
, puis on effectue
une intégration par partie sur les termes de plus haut degré. Il vient:
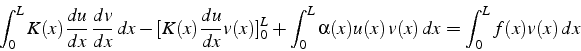
Le calcul du terme de bord se fait en utilisant les conditions aux
limites et en imposant à la fonction test ![]() d'être une variation
de la solution
d'être une variation
de la solution ![]() . Comme on impose la valeur de
. Comme on impose la valeur de ![]() en
en ![]() (
(![]() ), sa variation doit être nulle en ce point. La fonction
test
), sa variation doit être nulle en ce point. La fonction
test ![]() doit donc s'annuler en
doit donc s'annuler en ![]() . et le terme de bord
. et le terme de bord
![]() s'annulle. Le second terme de bord se calcule à l'aide de la seconde
condition aux limites:
s'annulle. Le second terme de bord se calcule à l'aide de la seconde
condition aux limites:
![]() .
La formulation faible de (4.19) s'écrit alors:
.
La formulation faible de (4.19) s'écrit alors:
Exercice: montrez que cette formulation faible est équivalente à la formulation variationnelle suivante:
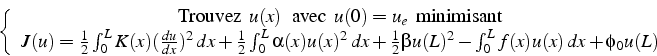
Pour construire l'approximation par éléments finis
![]() ,
on crée un maillage
,
on crée un maillage
![]() du domaine de calcul constitué
de
du domaine de calcul constitué
de ![]() segments de coordonnées
segments de coordonnées
![]() :
:
![\begin{displaymath}
\mathcal{M}^{h}=\bigcup_{k=1}^{ne}[x_{k},x_{k+1}] \mbox{ avec } x_{1}=0, x_{ne+1}=L\end{displaymath}](img714.png)
On note
![]() , l'élément
, l'élément ![]() du maillage de longueur
du maillage de longueur
![]() .
.
Remarque: on a choisit de numéroter les noeuds du maillage
de 1 à ![]() contrairement à l'exemple précédent, où on les avait
numéroté de 0 à
contrairement à l'exemple précédent, où on les avait
numéroté de 0 à ![]() . Ce choix sera justifier par la suite,lorsque
l'on programmera la méthode. En effet dans de nombreux langage de
programmation ( entre autre Maple et Matlab), les indices de tableaux
commencent à 1 et non pas à 0. D'autre part, contrairement au “calcul
à la main” précédent, nous ne chercherons pas à éliminer la valeur
au premier noeud de façon à conserver une approche générale.
. Ce choix sera justifier par la suite,lorsque
l'on programmera la méthode. En effet dans de nombreux langage de
programmation ( entre autre Maple et Matlab), les indices de tableaux
commencent à 1 et non pas à 0. D'autre part, contrairement au “calcul
à la main” précédent, nous ne chercherons pas à éliminer la valeur
au premier noeud de façon à conserver une approche générale.
Sur ce maillage, l'approximation ![]() par éléments finis
par éléments finis
![]() de la solution est définie par ses valeurs
de la solution est définie par ses valeurs
![]() aux
aux
![]() points nodaux
points nodaux
![]() , correspondant aux
extrémités des segments du maillage. Cette approximation possède donc
, correspondant aux
extrémités des segments du maillage. Cette approximation possède donc
![]() degrés de liberté
degrés de liberté ![]() correspondant aux
correspondant aux ![]() noeuds d'interpolation
noeuds d'interpolation ![]() .
.
Sur chaque élément ![]() cette approximation est définie à partir
des 2 fonctions de forme
cette approximation est définie à partir
des 2 fonctions de forme
![]() de l'élément
de l'élément
![]() (4.6) et du changement de variable
(4.6) et du changement de variable ![]() (4.5):
(4.5):
![\begin{eqnarray*}
u^{h}(x)=u_{k}N_{1}(\xi(x))+u_{k+1}N_{2}(\xi(x)) \mbox{ pou...
... e_{k}=[x_{k},x_{k+1}]\\
\xi(x)=2\frac{x-x_{k}}{x_{k+1}-x_{k}}-1\end{eqnarray*}](img729.png)
L'approximation globale est la somme de ces approximations élémentaires
et s'écrit en fonction des fonctions de base ![]() :
:
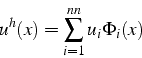
La fonction de base ![]() est associée au noeud
est associée au noeud ![]() du maillage et est définie à partir des fonctions de forme
du maillage et est définie à partir des fonctions de forme ![]() par les relations:
par les relations:
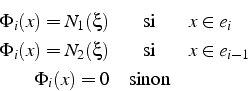
Le programme 4.2.2 implémente sous Maple l'interpolation
éléments finis
![]() sur un maillage de
sur un maillage de ![]() éléments.
éléments.
# Approximation par éléments finis > with(linalg): with(plots): # Nombre d'éléments Ne > L:=3; Ne:=8; # Maillage et coordonnees des pts de maillage > h:=L/Ne; Xp:=[seq(i*h,i=0..Ne)]; # d=degre d'interpolation, Nn=Nombre de noeuds, X=coordonnees des nds > d:=1; Nn:=Ne+1;X:=evalm(Xp): # num=numérotation par élément et long=longueur de chaque element > num:=k->[k,k+1]; long:=k->Xp[k+1]-Xp[k]; # Fonctions de forme de l'element P1 > N1:=unapply(interp([-1,1],[1,0],xi),xi); > N2:=unapply(interp([-1,1],[0,1],xi),xi); # Transformation x=x(xi) vers l'element de reference [-1,1] > Xi:=unapply(N1(xi)*'Xp'[i]+N2(xi)*'Xp'[i+1],xi,i); # Interpolation G d'une fonction g(x) sur le maillage > Interpol:=proc(g) > global Nn: > local G,i; > G:=vector(Nn,0): > for i from 1 to Nn do G[i]:=g(X[i]); end; > return evalm(G); > end proc: # Calcul de la norme de l'erreur d'interpolation: f(x)=fonction # et F= interpolation (calcul sur l'elt de reference) > Erreur:=proc(f,F) > global Ne,Xp; > local err,k,h; > err:=0; > for k from 1 to Ne do > h:=(Xp[k+1]-Xp[k])/2.0; > err:=err+h* > evalf(Int((f(Xi(xi,k))-(F[k]*N1(xi)+F[k+1]*N2(xi)))^2, > xi=-1..1)); > end: > return sqrt(err); > end: > # Example: fonction cos(2x) > f:=x->cos(2.0*x); > F:=Interpol(f); > P1:=plot(f(x),x=0..L): > P2:=plot([seq([X[i],F[i]],i=1..Nn)],style=point,color=blue): > display(P1,P2); > err:=Erreur(f,F);
Le programme est écrit de façon modulaire et général, de telle sorte
que l'on puisse très facilement implémenter une interpolation de degré
![]() quelconque. Pour cela on introduit comme variable le degré
quelconque. Pour cela on introduit comme variable le degré ![]() du polynôme d'interpolation (ligne 8), et on distingue les noeuds
du maillage, que l'on note
du polynôme d'interpolation (ligne 8), et on distingue les noeuds
du maillage, que l'on note ![]() (ligne 6), des points d'interpolation,
que l'on note
(ligne 6), des points d'interpolation,
que l'on note ![]() (ligne 8). On introduit ensuite 2 fonctions (ligne
10): la fonction
(ligne 8). On introduit ensuite 2 fonctions (ligne
10): la fonction ![]() qui pour un élément
qui pour un élément ![]() renvois les numéros
des points d'interpolation de l'élément, et la fonction
renvois les numéros
des points d'interpolation de l'élément, et la fonction ![]() qui calcul simplement la longueur
qui calcul simplement la longueur ![]() de l'élément
de l'élément ![]() . On calcule
ensuite les fonctions de forme de l'élément
. On calcule
ensuite les fonctions de forme de l'élément
![]() comme
polynômes de Lagrange en utilisant la fonction Maple interp
(lignes 12,13). La transformation de l'élément
comme
polynômes de Lagrange en utilisant la fonction Maple interp
(lignes 12,13). La transformation de l'élément ![]() vers l'élément
de référence
vers l'élément
de référence ![]() est noté
est noté ![]() (ligne 15):
(ligne 15):
On écrit ensuite une fonction ![]() qui calcul le vecteur
qui calcul le vecteur
![]() des valeurs d'une fonction f(x) aux points d'interpolation:
des valeurs d'une fonction f(x) aux points d'interpolation:
![]() (lignes
17 à 23).
(lignes
17 à 23).
Enfin on écrit une fonction ![]() qui calcule la norme de
l'erreur entre une fonction
qui calcule la norme de
l'erreur entre une fonction ![]() et son approximation
et son approximation ![]() sur le maillage élément finis. On choisit comme norme, l'intégrale
du carré de la différence (norme
sur le maillage élément finis. On choisit comme norme, l'intégrale
du carré de la différence (norme ![]() ):
):
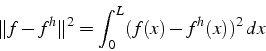
Cette norme mesure l'erreur moyenne sur le domaine de calcul. Pour
cela on calcule l'intégrale élément par élément, en éffectuant pour
chaque élément la transformation vers l'élément de référence. Pour
une approximation
![]() sur un élément
sur un élément
![]() ,
on a:
,
on a:
et l'erreur sur un élément s'écrit:
![\begin{displaymath}
\Vert f-f^{h}\Vert_{e_{k}}^{2}=\frac{h_{k}}{2}\int_{-1}^{+1}(f(x(\xi)-(F[k]*\Phi_{1}(\xi)+F[k+1]*\Phi_{2}(\xi))^{2}dx\end{displaymath}](img748.png)
Le calcul de cette intégrale est laissé à Maple. Pour cela on a utilisé
la fonction d'intégration ![]() sous sa forme directe d'intégration
numérique i.e.
sous sa forme directe d'intégration
numérique i.e.
![]() (ligne 33). Cela évite que Maple
cherche tout d'abord à effectuer une intégration analytique, puis
calcule ensuite la valeur numérique. On gagne ainsi un factor 5 à
10 en temps de calcul, ce qui n'est pas négligeable pour des maillages
importants.
(ligne 33). Cela évite que Maple
cherche tout d'abord à effectuer une intégration analytique, puis
calcule ensuite la valeur numérique. On gagne ainsi un factor 5 à
10 en temps de calcul, ce qui n'est pas négligeable pour des maillages
importants.
La fin du programme est un exemple d'interpolation d'une fonction
![]() sur un maillage de 10 éléments de
sur un maillage de 10 éléments de ![]() Les fonctions
de base et l'interpolation sont données sur la figure (4.13).
L'erreur d'interpolation vaut dans ce cas:
Les fonctions
de base et l'interpolation sont données sur la figure (4.13).
L'erreur d'interpolation vaut dans ce cas:
![]()
Exercice: calculer l'erreur d'interpolation pour des maillages de plus en plus fins.
La solution approchée ![]() par éléments finis
par éléments finis
![]() de (4.20) s'écrit sous la forme:
de (4.20) s'écrit sous la forme:
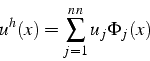
Elle doit vérifier les conditions aux limites fortes ( i.e. la condition
de Dirichlet en ![]() :
:
![]() ). En notant à nouveau que
les fonctions de bases vérifient
). En notant à nouveau que
les fonctions de bases vérifient
![]() , cette
condition impose la valeur nodale de
, cette
condition impose la valeur nodale de ![]() au noeud
au noeud ![]() du maillage:
du maillage:
Les fonctions tests associées ![]() étant des variations de
étant des variations de ![]() ,
elles doivent donc s'annuller en
,
elles doivent donc s'annuller en ![]() . Elles s'écrivent sous la
forme générale suivante:
. Elles s'écrivent sous la
forme générale suivante:
Ces fonctions tests sont des combinaisons linéaires des ![]() fonctions
de base
fonctions
de base
![]() . En remplaçant dans la formulation
faible (4.20) la solution exacte
. En remplaçant dans la formulation
faible (4.20) la solution exacte ![]() par la solution approchée
par la solution approchée
![]() donnée par (4.21) et la fonction test
donnée par (4.21) et la fonction test ![]() par
une de ces
par
une de ces ![]() fonctions de base
fonctions de base
![]() ,
on obtient la formulation faible discrète:
,
on obtient la formulation faible discrète:
Pour obtenir cette relation on a permuté la sommation
![]() et l'intégration
et l'intégration ![]() et on a sortie les coefficients
et on a sortie les coefficients ![]() des intégrales. D'autre part on a remplacé
des intégrales. D'autre part on a remplacé ![]() par sa valeur
par sa valeur
![]() . L'équation (4.23) écrite pour
. L'équation (4.23) écrite pour ![]() est un
système linéaire de
est un
système linéaire de ![]() inconnues
inconnues
![]() (en notant
que
(en notant
que ![]() est fixé par la condition aux limites), qu'il suffit
de résoudre pour obtenir la solution approchée
est fixé par la condition aux limites), qu'il suffit
de résoudre pour obtenir la solution approchée ![]() . De façon
à construire un programme le plus général possible, on considérera
que l'on a
. De façon
à construire un programme le plus général possible, on considérera
que l'on a ![]() inconnues
inconnues ![]() , qui sont données par les
, qui sont données par les ![]() équations (4.23) auxquelles on ajoute l'équation supplémentaire
équations (4.23) auxquelles on ajoute l'équation supplémentaire
![]() . Dans cette approche on construit un système linéaire
de
. Dans cette approche on construit un système linéaire
de ![]() inconnues à
inconnues à ![]() équations. Dans un premier temps cela permettra
de construire la matrice
équations. Dans un premier temps cela permettra
de construire la matrice ![]() et le second membre
et le second membre ![]() du système linéaire sans tenir compte des conditions aux limites et
donc de façon générique. Puis dans un second temps, on appliquera
les conditions aux limites sur le système linéaire: i.e. on remplacera
la première équation par l'équation
du système linéaire sans tenir compte des conditions aux limites et
donc de façon générique. Puis dans un second temps, on appliquera
les conditions aux limites sur le système linéaire: i.e. on remplacera
la première équation par l'équation ![]() et on introduira
le terme lié à la conditions aux limites en
et on introduira
le terme lié à la conditions aux limites en ![]()
Les coefficients génériques de ![]() et de
et de ![]() s'écrivent:
s'écrivent:
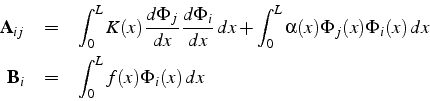
Pour calculer ces coefficients, on effectue un calcul élément par
élément en déterminant les matrices élémentaires et les second membres
élémentaires sur un élément ![]() . Les calculs des intégrales
font intervenir des coefficients variables
. Les calculs des intégrales
font intervenir des coefficients variables ![]() et
et ![]() et nous utiliserons Maple pour calculer les intégrales faisant intervenir
ces coefficients. Une autre approche consisterait à calculer une approximation
éléments finis de ces coefficients sur chaque élément, ou à choisir
une valeur moyenne par élément.
et nous utiliserons Maple pour calculer les intégrales faisant intervenir
ces coefficients. Une autre approche consisterait à calculer une approximation
éléments finis de ces coefficients sur chaque élément, ou à choisir
une valeur moyenne par élément.
Exercice: comparer le calcul de la matrice élémentaire
de raideur avec une approximation de ![]() constante,
constante,
![]() et exacte dans le cas où
et exacte dans le cas où ![]() est un polynôme de degré 1 et 2.
est un polynôme de degré 1 et 2.
Pour le second membre ![]() , nous utiliserons une approximation
, nous utiliserons une approximation
![]() sur le maillage éléments finis:
sur le maillage éléments finis:
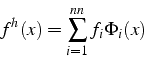
Sur un élément ![]() la matrice élémentaire est la somme d'une
matrice de rigidité
la matrice élémentaire est la somme d'une
matrice de rigidité
![]() et d'une matrice de masse
et d'une matrice de masse
![]() ,
qui pour des éléments finis
,
qui pour des éléments finis
![]() sont des matrices
2*2 puisqu'il y a 2 fonctions de forme
sont des matrices
2*2 puisqu'il y a 2 fonctions de forme
![]() associées
aux 2 points d'interpolations de numéros
associées
aux 2 points d'interpolations de numéros
![]() (figure4.6)
:
(figure4.6)
:
De façon générale, pour des éléments finis
![]() , les matrices élémentaires sont des matrices
, les matrices élémentaires sont des matrices ![]() puisqu'il
faut
puisqu'il
faut ![]() de points d'interpolation (de numéros
de points d'interpolation (de numéros
![]() pour définir un polynôme de degré
pour définir un polynôme de degré ![]() , et que l'on a donc
, et que l'on a donc ![]() fonctions de forme
fonctions de forme
![]() .
.
Avec ces notations, de façon générique (i.e. valable pour un approximation
![]() ,
,
![]() ,
,![]()
![]() ),
les matrices élémentaires s'écrivent:
),
les matrices élémentaires s'écrivent:
Le programme 4.2.4 ci-dessous implémente le calcul de la matrice de rigidité, en programmant la relation (4.24) comme une procédure Maple. On laisse Maple effectuer les intégrations des fonctions de formes. On note enfin que pour renvoyer la valeur de la matrice élémentaire (et non son nom), on utilise la fonction evalm.
# Matrice élémentaire de rigidite > MatRigidite:=proc(k,K) > global d; # dimension de l'interpolation > local Ke,p,q,h; > h:=long(k); > Ke:=matrix(d+1,d+1,0); > for p from 1 to d+1 do > for q from 1 to d+1 do > Ke[p,q]:=2.0/h* > int(K(Xi(xi,k))*diff(N||p(xi),xi)*diff(N||q(xi),xi),xi=-1..1); > end; > end; > return evalm(Ke); > end; >
Si la fonction ![]() est contante, on retouve pour des éléments
est contante, on retouve pour des éléments
![]() la matrice élémentaire suivante:
la matrice élémentaire suivante:
![\begin{displaymath}
\mathbf{K}^{k}=\frac{K}{h^{k}}\left[\begin{array}{cc}
1 & -1\\
-1 & 1\end{array}\right]\end{displaymath}](img785.png)
De même le programme 4.2.4 ci-dessous implémente le calcul de la matrice de masse, en programmant la relation (4.25) .
# Matrice élémentaire de masse > MatMasse:=proc(k,alpha) > global d; # dimension de l'interpolation > local Me,p,q,h > h:=long(k); > Me:=matrix(d+1,d+1,0); > for p from 1 to d+1 do > for q from 1 to d+1 do > Me[p,q]:=h/2.0* > int(alpha(Xi(xi,k))*N||p(xi)*N||q(xi),xi=-1..1); > end; > end; > return evalm(Me); > end;
Si la fonction ![]() est constante, on retouve pour des éléments
est constante, on retouve pour des éléments
![]() la matrice élémentaire suivante:
la matrice élémentaire suivante:
![\begin{displaymath}
\mathbf{M}^{k}=\alpha h^{k}\left[\begin{array}{cc}
1/3 & 1/6\\
1/6 & 1/3\end{array}\right]\end{displaymath}](img786.png)
Le calcul du second membre élémentaire procède de la même démarche.
Pour un élément
![]() , de sommets
, de sommets ![]() ,
l'approximation de
,
l'approximation de ![]() sur un élément
sur un élément ![]() s'écrit en variable
s'écrit en variable
![]() :
:
Pour un élément de degré ![]() , l'approximation de
, l'approximation de ![]() s'écrit:
s'écrit:
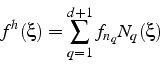
d'où l'on déduit le second membre élémentaire générique :
Le programme 4.2.5 ci-dessous implémente le calcul de ce vecteur élémentaire, en programmant la relation (4.26)
# Second membre elementaire > SmbElem:=proc(k,F) > global d; # dimension de l'interpolation > local Be,q,p,h,noi,ni; > h:=long(k); noi:=num(k); > Be:=vector(d+1,0); > for q from 1 to d+1 do > ni:=noi[q+1]; > for p from 1 to d+1 do > Be[p]:=Be[p]+ > F[ni]*h/2*int(N||q(xi)*N||p(xi),xi=-1..1); > end; > end; > return evalm(Be); > end;
Dans le cas d'une approximation
![]() , on trouve
l'expression:
, on trouve
l'expression:
![\begin{displaymath}
\mathbf{B}^{k}=\frac{h_{k}}{6}\left[\begin{array}{c}
2f_{k}+f_{k+1}\\
f_{k}+2f_{k+1}\end{array}\right]\end{displaymath}](img792.png)
Exercice: démontrer cette dernière relation.
Le calcul de la matrice globale ![]() et du second membre
et du second membre
![]() s'effectue par une procédure générale d'assemblage,
qui calcule les matrices élémentaires élément par élément et ensuite
insère les coefficients de ces matrices à la bonne place dans la matrice
globale.
s'effectue par une procédure générale d'assemblage,
qui calcule les matrices élémentaires élément par élément et ensuite
insère les coefficients de ces matrices à la bonne place dans la matrice
globale.
Pour un élément ![]() de type
de type
![]() ayant comme
numéro de sommets
ayant comme
numéro de sommets
![]() , la matrice élémentaire
, la matrice élémentaire
![]() de dimension
de dimension ![]() contribue aux coefficients
de la matrice globale A suivants:
contribue aux coefficients
de la matrice globale A suivants:
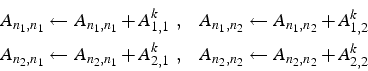
Par exemple, sur le maillage de la figure (4.12), la matrice
élémentaire
![]() sur l'élément
sur l'élément ![]() contribue aux 4 coefficients
suivants de
contribue aux 4 coefficients
suivants de ![]() :
:

L'algorithme d'assemblage général (1) est donnée ci dessous
ainsi que le programme Maple 4.2.6 associé. On notera que
l'on a fait varier les indices ![]() et
et ![]() à partir de 1 (et non
de 0), pour tenir compte du fait que sous Maple (et Matlab) les indices
des tableaux commencent à 1.
à partir de 1 (et non
de 0), pour tenir compte du fait que sous Maple (et Matlab) les indices
des tableaux commencent à 1.
A l'issue de cet assemblage la matrice ![]() et le second
membre
et le second
membre ![]() calculée avec les paramètres de l'exemple précédent
calculée avec les paramètres de l'exemple précédent
s'écrivent pour un maillage de ![]() éléments:
éléments:
![\begin{displaymath}
\mathbf{A}=\left[\begin{array}{ccccccccc}
507.0 & -501.0 & 0...
... 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & -501.0 & 507.0\end{array}\right]\end{displaymath}](img810.png)
Cette matrice est symétrique et tri diagonale (car avec l'interpolation
![]() , une fonction de base associée à un noeud ou degré
de liberté
, une fonction de base associée à un noeud ou degré
de liberté ![]() est non nulle sur l'intervalle
est non nulle sur l'intervalle
![]() ).
).
Exercise: démontrer cette propriété
# Boucle d'assemblage > A:=matrix(Nn,Nn,0): B:=vector(Nn,0): > for k from 1 to Ne do > Ke:=MatRigidite(k,K); > Me:=MatMasse(k,alpha); > Be:=SmbElem(k,Vf); > noi:=num(k); > for p from 1 to d+1 do > ni:=noi[p]; > for q from 1 to d+1 do > nj:=noi[q]; > A[ni,nj]:=A[ni,nj]+Ke[p,q]+Me[p,q]; > end; > B[ni]:=B[ni]+Be[p]; > end; > end: >
Le calcul précédent est générique et ne tiens pas compte des conditions
aux limites. Pour la condition aux limites de Dirichlet en ![]() ,
on remplace la première équation par la condition:
,
on remplace la première équation par la condition:
ce qui reviens à annuler la première ligne de la matrice ![]() ,
puis à mettre un 1 sur le terme diagonale
,
puis à mettre un 1 sur le terme diagonale
![]() , et
, et ![]() dans
dans
![]() . Pour la condition aux limites en
. Pour la condition aux limites en ![]() (condition
mixte), il faut rajouter un terme dans la matrice
(condition
mixte), il faut rajouter un terme dans la matrice ![]() correspondant
à :
correspondant
à :
qui est non nul uniquement pour ![]() . Il faut donc modifier uniquement
le terme diagonale
. Il faut donc modifier uniquement
le terme diagonale ![]() :
:
Pour le second membre ![]() , il faut rajouter le terme
, il faut rajouter le terme
qui est non nul uniquement pour ![]() . Il faut donc modifier uniquement
le dernier terme de
. Il faut donc modifier uniquement
le dernier terme de ![]()
Le petit programme Maple 4.2.7 correspondant s'écrit:
# Conditions aux limites > for j from 1 to Nn do A[1,j]:=0; end: A[1,1]:=1; B[1]:=ue; > A[Nn,Nn]:=A[Nn,Nn]+beta; B[Nn]:=B[Nn]-phi; # Résolution > Uh:=evalf(linsolve(A,B));
Après application des conditions aux limites, la matrice ![]() s'écrit:
s'écrit:
![\begin{displaymath}
\mathbf{A}=\left[\begin{array}{ccccccccc}
1.0 & 0.0 & 0.0 & ...
... 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & -501.0 & 507.0\end{array}\right]\end{displaymath}](img824.png)
et le second membre ![]() :
:
On constate que la matrice ![]() n'est plus symétrique, à cause de
la façon d'implémenter la condition aux limites de Dirichlet. Nous
verrons dans le chapitre suivant comment imposer cette condition en
conservant la symétrie.
n'est plus symétrique, à cause de
la façon d'implémenter la condition aux limites de Dirichlet. Nous
verrons dans le chapitre suivant comment imposer cette condition en
conservant la symétrie.
Avec les paramètres suivants donnés dans le programme Maple 4.2.8
ci-dessous, pour un maillage de ![]() éléments
éléments
# Parametres du problème > L:=3; dd:=0.2;h:=50;Ta:=20;Te:=60; phie:=32; > K:=evalf(6000.0*Pi*dd^2/4): alpha:=evalf(h*Pi*dd): > f:=alpha*Ta: ue:=Te: beta:=0:phi:=phie: # Vecteurs des parametres interpolés sur le maillage > Vf:=Interpol(f):
la solution obtenue vaut:
La comparaison de cette solution éléments finis avec la solution exacte est donnée sur la figure (4.15).
On constate que l'erreur moyenne est très faible et vaut
Pour étudier la précision de la méthode des éléments finis
![]() ,
nous avons calculer l'erreur relative moyenne:
,
nous avons calculer l'erreur relative moyenne:
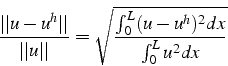
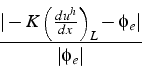
en fonction du nombre d'éléments ![]() du maillage pour des maillages
régulièrement espacés (i.e. la taille
du maillage pour des maillages
régulièrement espacés (i.e. la taille ![]() des éléments est proportionnelle
à
des éléments est proportionnelle
à ![]() ). Les résultats sont tracés en échelle logarithmique sur
la figure (4.16). On constate que l'erreur relative moyenne
varie en
). Les résultats sont tracés en échelle logarithmique sur
la figure (4.16). On constate que l'erreur relative moyenne
varie en
![]() (i.e. en
(i.e. en ![]() ) (comparaison
avec une droite de pente
) (comparaison
avec une droite de pente ![]() ), et que l'erreur relative sur la condition
aux limites varie en
), et que l'erreur relative sur la condition
aux limites varie en ![]() (i.e. en
(i.e. en ![]() ). Ce résultat
montre que l'approximation par éléments finis
). Ce résultat
montre que l'approximation par éléments finis ![]() converge vers
la solution exacte et que cette convergence est d'ordre 2. Ce résultat
est cohérent avec l'erreur d'interpolation, qui comme nous l'avons
vu est d'ordre 2 pour une approximation
converge vers
la solution exacte et que cette convergence est d'ordre 2. Ce résultat
est cohérent avec l'erreur d'interpolation, qui comme nous l'avons
vu est d'ordre 2 pour une approximation
![]() . On peut
en fait démontrer que l'erreur par éléments finis est majoré par cette
erreur d'interpolation.
. On peut
en fait démontrer que l'erreur par éléments finis est majoré par cette
erreur d'interpolation.