suivant: 3.2 Éléments finis monter: 3. Méthode des éléments précédent: 3. Méthode des éléments Table des matières
On veut calculer la température ![]() dans un barreau de longueur
dans un barreau de longueur
![]() , de section
, de section ![]() et de conductivité
et de conductivité ![]() dont l'extrémité gauche
est isotherme (i.e
dont l'extrémité gauche
est isotherme (i.e ![]() ), et l'extrémité droite reçoit un
flux de chaleur
), et l'extrémité droite reçoit un
flux de chaleur ![]() . En plus de la conduction dans le solide
(le flux de chaleur par conduction dans une section s'écrit
. En plus de la conduction dans le solide
(le flux de chaleur par conduction dans une section s'écrit
![]() ),
le barreau échange de la chaleur par convection avec l'air ambiant
à la température
),
le barreau échange de la chaleur par convection avec l'air ambiant
à la température ![]() sur toute sa longueur. En notant
sur toute sa longueur. En notant ![]() le
coefficient d'échange par convection par unité de surface, le flux
de chaleur par convection s'écrit pour un élément de longueur
le
coefficient d'échange par convection par unité de surface, le flux
de chaleur par convection s'écrit pour un élément de longueur ![]() :
:
![]() (où
(où ![]() est le périmètre de la
section du barreau)).
est le périmètre de la
section du barreau)).
En notant ![]() , et
, et ![]() , l'équation d'équilibre s'écrit:
trouver
, l'équation d'équilibre s'écrit:
trouver ![]() solution du système (4.1 )
solution du système (4.1 )
La formulation faible de ce problème s'obtient en multipliant l'équation
par une fonction test ![]() , et en intégrant sur le domaine d'étude.
Il vient:
, et en intégrant sur le domaine d'étude.
Il vient:
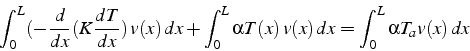
Pour tenir compte des conditions aux limites et symétriser le problème, on effectue une intégration par partie sur les termes de plus haut degré:

Si le problème est bien posé, le terme de bord
![]() doit pouvoir se calculer en fonction des conditions aux limites. Pour
cela on interprète la fonction test
doit pouvoir se calculer en fonction des conditions aux limites. Pour
cela on interprète la fonction test ![]() comme une variation
comme une variation ![]() de la solution
de la solution ![]() . Si on fixe la valeur de la solution en un
point (condition de Dirichlet), sa variation est nulle et la fonction
test
. Si on fixe la valeur de la solution en un
point (condition de Dirichlet), sa variation est nulle et la fonction
test ![]() doit s'annuler en ce point. Pour notre problème, on doit
donc imposer à
doit s'annuler en ce point. Pour notre problème, on doit
donc imposer à ![]() de s'annuller en
de s'annuller en ![]() puisque la valeur de
puisque la valeur de
![]() est fixée en ce point. Par contre en
est fixée en ce point. Par contre en ![]() , on impose aucune
contrainte sur
, on impose aucune
contrainte sur ![]() et on utilise la condition de flux pour calculer
le terme de bord. C'est une condition à la limite naturelle ou condition
de Neuman. Avec ces conditions, le terme de bord se réduit à
et on utilise la condition de flux pour calculer
le terme de bord. C'est une condition à la limite naturelle ou condition
de Neuman. Avec ces conditions, le terme de bord se réduit à ![]() ,
et la formulation faible s'écrit:
,
et la formulation faible s'écrit:
On remarque que dans cette formulation, seule la condition au limite
en ![]() est imposé de façon explicite. On parle alors de condition
forte. La condition en
est imposé de façon explicite. On parle alors de condition
forte. La condition en ![]() n'est pas imposée explicitement, mais
est prise en compte dans la formulation intégrale. C'est une condition
naturelle.
n'est pas imposée explicitement, mais
est prise en compte dans la formulation intégrale. C'est une condition
naturelle.
Exercice: Montrer que la formulation faible (4.2) est équivalente au problème de minimisation (4.3)
Pour résoudre le problème (4.2) (dont il n'existe en général
pas de solution analytique), on recherche une solution numérique approchée
![]() . En éléments finis, cette solution approchée est construite
à partir de 2 données:
. En éléments finis, cette solution approchée est construite
à partir de 2 données:
![\begin{displaymath}
\Omega=\bigcup_{i=1}^{ne}[x_{i-1},x_{i}]\end{displaymath}](img522.png)
Sur chaque segment, on choisit une interpolation polynômiale. Le type de l'interpolation dépend du problème à traiter. Pour notre problème elle doit en particulier respecter les points suivants:
La première condition impose que sur chaque élément le polynôme d'interpolation
![]() soit au moins de degré 1 pour pouvoir calculer les dérivées
premières de la solution qui interviennent dans la formulation faible
(4.2). Sur chaque élément
soit au moins de degré 1 pour pouvoir calculer les dérivées
premières de la solution qui interviennent dans la formulation faible
(4.2). Sur chaque élément
![]() , la solution
approchée est donc un polynôme
, la solution
approchée est donc un polynôme ![]() de degré
de degré ![]() .
.
Pour un polynôme d'ordre 1 sur
![]() (éléments finis
(éléments finis
![]() ), on utilise 2 points d'interpolation: les 2 extrémités
du segment
), on utilise 2 points d'interpolation: les 2 extrémités
du segment
![]() (figure 4.2).
(figure 4.2).
Exercice: déterminer les points d'interpolation pour un polynôme de degré 2, puis 3.
Considérons par exemple le maillage du domaine ![]() de
la figure (4.3) suivant:
de
la figure (4.3) suivant:
L'interpolation ![]() par éléments finis
par éléments finis
![]() d'une fonction
d'une fonction ![]() s'écrit:
s'écrit:
où
![]() sont les valeurs nodales de
sont les valeurs nodales de ![]() aux points de maillage
aux points de maillage
![]() . C'est une
fonction linéaire par morceau et continue sur l'intervalle d'étude
. C'est une
fonction linéaire par morceau et continue sur l'intervalle d'étude
![]() . Sa dérivée
. Sa dérivée
![]() s'écrit:
s'écrit:

C'est une fonction constante par morceau et discontinue aux points de maillage.
Exercice: calculer pour ce même maillage l'interpolation
par éléments finis
![]()
![\includegraphics[width=0.4\textwidth,height=0.3\textheight]{CHAP3/interp}](img540.png) ![\includegraphics[width=0.4\textwidth,height=0.3\textheight]{CHAP3/interp1}](img541.png)
|
Sur la figure (4.4), on a tracé l'interpolation par éléments
finis de la fonction
![]() et de sa dérivée sur ce
maillage de 3 segments en utilisant des polynômes de degré 1. On constate
que l'approximation
et de sa dérivée sur ce
maillage de 3 segments en utilisant des polynômes de degré 1. On constate
que l'approximation
![]() est bien continue, mais que
la dérivée est discontinue aux points de maillage.
est bien continue, mais que
la dérivée est discontinue aux points de maillage.
On rappelle que l'erreur entre une fonction ![]() et son polynôme
d'interpolation
et son polynôme
d'interpolation ![]() de degré
de degré ![]() sur l'intervalle
sur l'intervalle ![]() passant
par les
passant
par les ![]() points d'interpolation
points d'interpolation
![]() s'écrit:
s'écrit:
![\begin{displaymath}
f(x)-P(x)=\frac{\prod_{j=1}^{l+1}(x-x_{j})}{(l+1)!}f^{(l+1)}(\chi) \mbox{ avec }\chi\in[a,b]\end{displaymath}](img547.png)
Exercice: en étudiant la fonction
![]() ,
démontrer la formule précédente.
,
démontrer la formule précédente.
Pour une approximation linéaire sur un segment
![]() ,
l'erreur d'interpolation s'écrit
,
l'erreur d'interpolation s'écrit
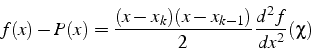
On vérifie que l'erreur s'annulle aux points d'interpolation et est
proportionnelle à la dérivée seconde de ![]()
A partir de cette relation locale, on peut déduire par calcul directe
les majorations d'erreurs suivantes pour la norme du maximum et la
norme moyenne de l'erreur sur l'intervalle
![]() de longueur
de longueur
![]() .
.
![\begin{eqnarray*}
\max_{x\in[x_{k-1},x_{k}]}(\vert f(x)-p(x)\vert) & \le & \frac...
...}\sqrt{\int_{x_{k-1}}^{x_{k}}(\frac{d^{2}f}{dx^{2}}(\chi))^{2}dx}\end{eqnarray*}](img552.png)
Exercice: en intégrant l'erreur d'interpolation, démontrer ces formules
On vérifie que l'erreur moyenne d'approximation par éléments finis
![]() est en
est en ![]() , i.e. est proportionnelle
au carré de la longueur des éléments en un point de l'intervalle.
, i.e. est proportionnelle
au carré de la longueur des éléments en un point de l'intervalle.
Exercice: montrez que l'erreur avec des éléments finis
![]() est en
est en ![]()
L'approximation par éléments finis est définie de façon locale sur
chaque élément (4.4). De façon à pouvoir la manipuler plus
facilement, on va l'exprimer de façon globale. Pour cela on détermine
une expression générique de l'approximation sur un élément
![]() .
.
Pour ce faire on introduit une transformation géométrique qui permet
de passer d'un élément quelconque
![]() à un élément
de référence
à un élément
de référence ![]() , sur lequel on va définir l'approximation de
manière générique.
, sur lequel on va définir l'approximation de
manière générique.
Cette transformation affine
![]() s'écrit:
s'écrit:
Pour une approximation
![]() , on a 2 points d'interpolation
et tout polynôme de degré 1
, on a 2 points d'interpolation
et tout polynôme de degré 1 ![]() s'écrit sur l'intervalle de
référence comme combinaision linéaire des 2 polynômes de Lagrange
s'écrit sur l'intervalle de
référence comme combinaision linéaire des 2 polynômes de Lagrange
![]() et
et ![]() associés à ces 2 points d'interpolations:
associés à ces 2 points d'interpolations:
Ce sont les deux “fonctions de forme” de l'élément
![]() . Le tracé de ces fonctions de forme est donné sur la figure (4.6).
. Le tracé de ces fonctions de forme est donné sur la figure (4.6).
Exercice: déterminer les 3 fonctions de formes pour
un élément
![]()
En utilisant le changement de variable ![]() (4.5),
un polynôme de degré 1 en x sur un élément
(4.5),
un polynôme de degré 1 en x sur un élément
![]() s'écrit:
s'écrit:
Attention: lorsque l'on calcule la dérivée de l'approximation
élément finis, la dérivée dans l'élément
![]() n'est
pas égale à la dérivée dans l'élément de référence. Il faut tenir
compte du changement de variable:
n'est
pas égale à la dérivée dans l'élément de référence. Il faut tenir
compte du changement de variable:

Pour un polynôme de degré 1, on obtient:
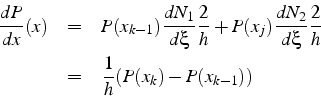
Exercice: calculer la dérivée d'une approximation élément
finis
![]()
Avec ces nouvelles notations, l'approximation élément finis ![]() de la fonction f(x) dans la relation (4.4) s'écrit
de la fonction f(x) dans la relation (4.4) s'écrit
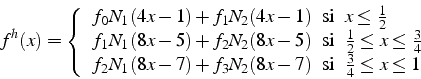
on constate que ![]() est une fonction linéaire des 4 valeurs nodales
est une fonction linéaire des 4 valeurs nodales
![]() . On peut donc écrire
. On peut donc écrire ![]() comme
une combinaison linéaire de ces valeurs:
comme
une combinaison linéaire de ces valeurs:
où les fonctions
![]() sont définies
par
sont définies
par
Exercice: pour ce même maillage, déterminer les fonctions
de base
![]()
Ces fonctions de base vérifient les propriétés importantes suivantes:
Nous allons maintenant chercher une approximation par éléments finis
de la solution du problème (4.2). Pour cela on choisit le
maillage suivant du domaine de calcul ![]() (c'est le même
maillage que précédemment, mais sur le domaine de calcul de longueur
(c'est le même
maillage que précédemment, mais sur le domaine de calcul de longueur
![]() du problème (4.2)):
du problème (4.2)):
On choisit ensuite sur ce maillage une approximation par élément finis
![]() de la solution approchée
de la solution approchée ![]() de (4.2).
Pour ce maillage de
de (4.2).
Pour ce maillage de ![]() éléments, le nombre de points nodaux est
égale à
éléments, le nombre de points nodaux est
égale à ![]() , et
, et ![]() s'écrit:
s'écrit:
On notera
![]() les valeurs nodales
les valeurs nodales
![]() ,
ce qui permet d'écrire
,
ce qui permet d'écrire ![]() sous la forme:
sous la forme:
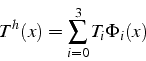
La solution du problème (4.2) doit vérifier les conditions aux limites fortes ( Dirichlet), i.e.:
La valeur nodale ![]() est donc fixée, et
est donc fixée, et ![]() s'écrit:
s'écrit:
Le problème discrétisé possède donc 3 degrés de liberté (ou inconnues):
les 3 valeurs nodales
![]() . De façon générale après
application des
. De façon générale après
application des ![]() conditions aux limites fortes, la solution élément
finis possède
conditions aux limites fortes, la solution élément
finis possède ![]() degré de liberté. Pour un maillage de
degré de liberté. Pour un maillage de ![]() éléments
éléments
![]() , on a
, on a ![]() .
.
En remplaçant la solution exacte par la solution approchée (4.9) dans l'équation (4.2) il vient la formulation faible discrète:
Ayant la forme (4.9) de la solution approchée
![]() ,
on peut en déduire les fonctions tests
,
on peut en déduire les fonctions tests ![]() associées, puisque
ce sont des variations
associées, puisque
ce sont des variations ![]() de
de ![]() qui s'écrivent:
qui s'écrivent:
On vérifie que ces fonctions tests s'annullent en ![]() (condition
de Dirichlet). Ces fonctions tests sont des combinaisons linéaires
des 3 fonctions de base
(condition
de Dirichlet). Ces fonctions tests sont des combinaisons linéaires
des 3 fonctions de base
![]() associées aux 3
degrés de liberté
associées aux 3
degrés de liberté
![]() .
.
En choisissant comme fonctions tests ![]() dans (4.10),
respectivement les 3 fonctions de base
dans (4.10),
respectivement les 3 fonctions de base
![]() ,
on obtient les 3 équations qui permettent de calculer les 3 inconnues
,
on obtient les 3 équations qui permettent de calculer les 3 inconnues
![]() :
:

C'est un système linéaire de 3 équations à 3 inconnues, qui s'écrit
après regroupement des termes sous la forme matricielle:
![]() ,
où la matrice
,
où la matrice ![]() le second membre
le second membre ![]() et le vecteur inconnu
et le vecteur inconnu ![]() sont donnés par:
sont donnés par:
![\begin{displaymath}
\mathbf{A}=\left[\begin{array}{ccc}
\int_{0}^{L}(K\frac{d\Ph...
...frac{d\Phi_{3}}{dx}+\alpha\Phi_{3}\Phi_{3})dx\end{array}\right]\end{displaymath}](img612.png)
![\begin{displaymath}
\mathbf{B}=\left[\begin{array}{c}
\int_{0}^{L}\alpha T_{a}\P...
...frac{d\Phi_{3}}{dx}+\alpha\Phi_{0}\Phi_{3})dx\end{array}\right]\end{displaymath}](img614.png)
soit sous forme générique:
On remarque que la matrice ![]() est symétrique puisque la
formulation faible est elle même symétrique en
est symétrique puisque la
formulation faible est elle même symétrique en ![]() et
et ![]() .
.
La solution de la formulation faible discrète (4.10) s'obtient
donc par résolution d'un système linéaire. Il nous reste à calculer
la matrice ![]() et le second membre
et le second membre ![]() . Connaissant
l'expression des fonctions de base (4.7), un calcul directe
des intégrales permettrait d'obtenir la matrice
. Connaissant
l'expression des fonctions de base (4.7), un calcul directe
des intégrales permettrait d'obtenir la matrice ![]() et le
vecteur
et le
vecteur ![]() . Cette approche n'est possible que pour un petit
nombre de degré de liberté, et on préfère utiliser une approche systématique
pour le calcul de
. Cette approche n'est possible que pour un petit
nombre de degré de liberté, et on préfère utiliser une approche systématique
pour le calcul de ![]() et
et ![]() , qui s'appelle l'assemblage.
, qui s'appelle l'assemblage.
Pour le calcul des coefficients ![]() et
et ![]() , nous allons
tout d'abord donner quelques propriétés des fonctions de base
, nous allons
tout d'abord donner quelques propriétés des fonctions de base ![]() (voir figure 4.8):
(voir figure 4.8):
D'après la relation (4.13), la calcul de ![]() fait intervenir
2 types d'intégrale. On décompose alors
fait intervenir
2 types d'intégrale. On décompose alors ![]() en 2 matrices:
en 2 matrices:

la matrice ![]() est appelée matrice de rigidité (ou de raideur)
et
est appelée matrice de rigidité (ou de raideur)
et ![]() matrice de masse.
matrice de masse.
Pour calculer ces intégrales on décompose l'intégrale sur le domaine
![]() en somme d'intégrales élémentaires sur chaque élément
en somme d'intégrales élémentaires sur chaque élément
![]() .
.

On est donc ramené à un calcul d'intégrales élémentaires sur chaque
élément. En utilisant les propriétés des fonctions de base ![]() ,
chaque intégrale élémentaire est non nulle sur un élément
,
chaque intégrale élémentaire est non nulle sur un élément
![]() si et seulement si les noeuds
si et seulement si les noeuds ![]() et
et ![]() appartiennent tous
les deux à cet élément. Pour des éléments
appartiennent tous
les deux à cet élément. Pour des éléments
![]() , on a
4 cas possibles:
, on a
4 cas possibles:
où ![]() et
et ![]() sont les numéros des 2 sommets de l'élément
sont les numéros des 2 sommets de l'élément
![]() .
.
Avec ces notations, et en utilisant les codes de couleur de la figure
(4.9) pour les éléments du maillage, le premier élément
de la matrice ![]() (4.12) s'écrit
(4.12) s'écrit

puisque le noeud 1 a pour support les éléments ![]() (
(![]() )
et
)
et ![]() (
(![]() ). Par contre l'élément
). Par contre l'élément ![]() s'écrit:
s'écrit:
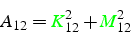
On a donc l'expression de ![]() sous la forme:
sous la forme:
![\begin{displaymath}
_{\mathbf{A}=\left[\begin{array}{ccc}
\color{red}K_{22}^{1} ...
...lack} & \color{blue}M_{22}^{3} \color{black}\end{array}\right]}\end{displaymath}](img647.png)
Il reste donc à calculer ces matrices élémentaires pour calculer ![]() .
Pour ce faire on revient à la définition (4.7) des fonctions
de base
.
Pour ce faire on revient à la définition (4.7) des fonctions
de base ![]() en fonction des fonctions de forme
en fonction des fonctions de forme ![]() en effectuant le changement de variable (4.5) sur l'élément
de référence. Sur un élément
en effectuant le changement de variable (4.5) sur l'élément
de référence. Sur un élément ![]()
![]() (de longueur
(de longueur
![]() ), on a:
), on a:
En effectuant le changement de variables ![]() (4.5)
dans l'intégrale, il vient:
(4.5)
dans l'intégrale, il vient:
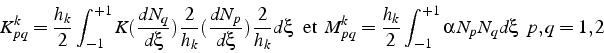
Ces deux matrices élémentaires sont symétriques. De plus la somme
des coefficients des lignes (et donc des colonnes) de
![]() est nulle parce que la somme des fonctions de forme
est nulle parce que la somme des fonctions de forme
![]() est égale à 1.
est égale à 1.
Exercice: démontrer que la somme des lignes (et des colonnes) de la matrice de rigidité est nulle
Pour des coefficients ![]() et
et ![]() constants, ces 2 matrices
élémentaires s'écrivent, après le calcul simple des intégrales:
constants, ces 2 matrices
élémentaires s'écrivent, après le calcul simple des intégrales:
![\begin{displaymath}
\mathbf{K}^{k}=\frac{K}{h_{k}}\left[\begin{array}{cc}
1 & -1...
...3} & \frac{1}{6}\\
\frac{1}{6} & \frac{1}{3}\end{array}\right]\end{displaymath}](img655.png)
Exercice: démontrer les expressions précédentes
En notant que les éléments du maillage ont pour longueur :
![]() ,
on obtient la matrice A suivante (en coloriant en rouge,
vert et bleu les contributions des éléments 1,2 et 3):
,
on obtient la matrice A suivante (en coloriant en rouge,
vert et bleu les contributions des éléments 1,2 et 3):
On vérifie la symétrie de la matrice.
Le calcul du second membre procède de la même démarche. Le calcul
des intégrales se fait élément par élément en tenant compte des propriétés
des fonctions de base. L'expression du second membre ![]() de (4.13) contient 2 types de termes:
de (4.13) contient 2 types de termes:
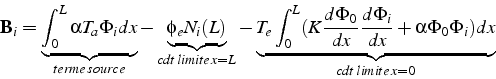
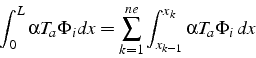
et on utilise les propriétés des fonctions de base ![]() . Pour
des éléments
. Pour
des éléments
![]() , ces intégrales élémentaires sur un
élément
, ces intégrales élémentaires sur un
élément ![]() sont non nulles uniquement si
sont non nulles uniquement si ![]() ou
ou ![]() . On a donc à calculer 2 intégrales élémentaires par élément, qui
s'écrivent sous la forme d'un vecteur second membre élémentaire:
. On a donc à calculer 2 intégrales élémentaires par élément, qui
s'écrivent sous la forme d'un vecteur second membre élémentaire:
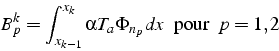
où ![]() et
et ![]() sont les 2 numéros des sommets de l'éélment
sont les 2 numéros des sommets de l'éélment
![]() .
.
Avec cette notation, le terme source du second membre ![]() s'écrit:
s'écrit:
![\begin{displaymath}
\mathbf{B}=\left[\begin{array}{c}
\color{red}B_{2}^{1} \colo...
...}\\
\color{blue}B_{3}^{2} \color{black}\end{array}\right]+C.L.\end{displaymath}](img661.png)
Pour le calcul des seconds membres élémentaires, on utilise le changement
de variable ![]() (4.5) sur l'élément de référence.
En utilisant la relation (4.16), il vient:
(4.5) sur l'élément de référence.
En utilisant la relation (4.16), il vient:

Si le coefficient ![]() et la température de l'air
et la température de l'air ![]() sont
constants, le second membre élémentaire s'écrit:
sont
constants, le second membre élémentaire s'écrit:
![\begin{displaymath}
\mathbf{B}_{p}^{k}=\alpha T_{a}h_{k}\left[\begin{array}{c}
\frac{1}{2}\\
\frac{1}{2}\end{array}\right]\end{displaymath}](img663.png)
Exercice: démontrer l'expression précédente.
On en déduit la contribution du terme source dans le second membre
![]()
![\begin{displaymath}
\mathbf{B}=\alpha T_{a}L\left[\begin{array}{c}
\color{red}\f...
...\
\color{blue}\frac{1}{8} \color{black}\end{array}\right]+C.L.\end{displaymath}](img664.png)
La contribution des termes liés aux conditions aux limites n'interviens
que sur certaines composantes de ![]() . La contribution de
la condition au limite en
. La contribution de
la condition au limite en ![]() fait intervenir le produit de la
fonction de base
fait intervenir le produit de la
fonction de base ![]() par une fonction de base
par une fonction de base ![]() .
Comme il a été indiqué dans les propriétés des fonctions de base,
ce produit est non nul uniquement pour
.
Comme il a été indiqué dans les propriétés des fonctions de base,
ce produit est non nul uniquement pour ![]() (et on a donc uniquement
une contribution dans
(et on a donc uniquement
une contribution dans
![]() ). L'intégrale se calcule sur
l'élément
). L'intégrale se calcule sur
l'élément ![]() :
:
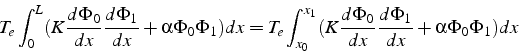
Ce terme correspond justement aux intégrales élémentaires (4.14)
et (4.15) pour l'élément
![]() multiplié
par
multiplié
par ![]() :
:
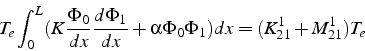
La contribution de la condition aux limites en ![]() fait intervenir
fait intervenir
![]() , qui est non nul uniquement pour
, qui est non nul uniquement pour ![]() . On a donc
uniquement une contribution dans
. On a donc
uniquement une contribution dans ![]() qui s'écrit:
qui s'écrit:
Le second membre complet s'écrit alors:
Pour la résolution numérique, on considère un barreau d'aluminium
de longueur ![]() , de diamètre
, de diamètre ![]() , dont le coefficient
de conductivité thermique vaut
, dont le coefficient
de conductivité thermique vaut
![]() . Il est maintenu
à une température
. Il est maintenu
à une température
![]() en
en ![]() et on impose un flux
de
et on impose un flux
de
![]() en
en ![]() . Il est refroidit dans l'air à température
ambiante
. Il est refroidit dans l'air à température
ambiante
![]() par convection forcée avec
par convection forcée avec
![]() (pour de la convection naturelle
(pour de la convection naturelle
![]() ).
).
Pour vérifier le calcul précédent, nous allons tout d'abord ne pas
tenir compte de la convection (i.e. ![]() ). Dans ce cas la solution
exacte de l'équation (4.1) est triviale. La répartition de
température est linéaire et vérifie:
). Dans ce cas la solution
exacte de l'équation (4.1) est triviale. La répartition de
température est linéaire et vérifie:
Le système linéaire discret s'écrit:
![\begin{displaymath}
\left[\begin{array}{ccc}
376.99 & -251.33 & 0\\
-251.33 & 5...
...\left[\begin{array}{c}
7539.82\\
0\\
-32.00\end{array}\right]\end{displaymath}](img687.png)
ce qui donne après résolution la répartition de température suivante:
![\begin{displaymath}
\left[\begin{array}{c}
T_{1}\\
T_{2}\\
T_{3}\end{array}\ri...
...left[\begin{array}{c}
59.74\\
59.61\\
59.49\end{array}\right]\end{displaymath}](img688.png)
C'est exactement la solution analytique aux noeuds du maillage
![]() .
On constate ainsi que si la solution exacte est linéaire, la solution
par éléments finis est égale à la solution exacte. Cela est naturelle,
car l'approximation par élément finis
.
On constate ainsi que si la solution exacte est linéaire, la solution
par éléments finis est égale à la solution exacte. Cela est naturelle,
car l'approximation par élément finis
![]() approche
exactement une solution linéaire. On note aussi que la variation de
température dans la barre est très faible dans ce cas (de l'ordre
approche
exactement une solution linéaire. On note aussi que la variation de
température dans la barre est très faible dans ce cas (de l'ordre
![]() ), car le flux de chaleur en sortie
), car le flux de chaleur en sortie ![]() est
faible .
est
faible .
Dans le cas ![]() et avec des coefficients constants, on peut
encore déterminer la solution analytique. Les calculs sont un peu
plus complexes, et on donne le programme Maple 4.1.6 ci dessous
qui permet de calculer cette solution.
et avec des coefficients constants, on peut
encore déterminer la solution analytique. Les calculs sont un peu
plus complexes, et on donne le programme Maple 4.1.6 ci dessous
qui permet de calculer cette solution.
# Programme Maple pour le calcul de la solution annalytique
> restart:
# Equation du problème
> -K*diff(T(x),x$2)+alpha*T(x)=alpha*Ta;eq:=%:
# Solution générale
> dsolve(eq,T(x)):Tex:=unapply(rhs(%),x);
# Determination des constantes avec les conditions aux limites
> Tex(0)=Te;
> K*D(Tex)(L)=phi;
> S:=simplify(solve({%,%%},{_C1,_C2})):
> Tex:=unapply(simplify(subs(S,Tex(x)),trig),x);
# Application
> L:=3; K:=evalf(6000*Pi*0.2^2/4); alpha:=evalf(50.0*Pi*0.2);
> Ta:=20; Te:=60; phi:=-32;
> plot(Tex(x),x=0..L,title="solution exacte");
Avec ce programme, on obtient l'expression suivante pour la solution
exacte ![]() :
:
En remplaçant les valeurs numériques dans la matrice (4.17) et le second membre (4.18), on obtient le système suivant pour la solution approchée par éléments finis:
![\begin{displaymath}
\left[\begin{array}{ccc}
400.56 & -247.40 & 0.0\\
-247.40 &...
...[\begin{array}{c}
7775.44\\
471.24\\
203.62\end{array}\right]\end{displaymath}](img693.png)
ce qui donne après résolution la répartition de température approchée
![]() :
:
![\begin{displaymath}
\left[\begin{array}{c}
T_{1}\\
T_{2}\\
T_{3}\end{array}\ri...
...left[\begin{array}{c}
45.51\\
42.26\\
41.12\end{array}\right]\end{displaymath}](img694.png)
La solution analytique pour ces mêmes points de calcul vaut:
![\begin{displaymath}
\left[\begin{array}{c}
T_{1}\\
T_{2}\\
T_{3}\end{array}\ri...
...left[\begin{array}{c}
45.67\\
42.42\\
41.28\end{array}\right]\end{displaymath}](img695.png)
La solution exacte étant de type exponentielle, l'approximation par
éléments finis ne peut pas donner la solution exacte. On constate
cependant que dans ce cas la solution élément finis est très précise,
puisque l'erreur nodale est inférieure à ![]() (i.e. un
écart relatif de
(i.e. un
écart relatif de ![]() ).
).
Quelques remarques:
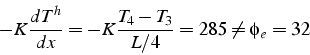
On montrera dans la suite que les conditions aux limites naturelles sont vérifiées exactement par la solution approchée que lorsque le maillage devient très fin: i.e. à la limite quand la solution approchée tends vers la solution exacte.