3.4 Applications au cas de coefficients non constants

Pour terminer cette étude, nous allons appliquer la méthode des éléments finis pour résoudre le problème précédent dans le cas où la section du barreau est variable: i.e. $S=S(x)$, et l'extrémité $x=L$ est à l'air libre. Ce problème est un problème classique d'ailette de radiateur, qui permet d'évacuer la chaleur d'un support à une température $T_{e}$ par échange convectif avec l'air ambiant à température $T_{a}$.

Figure 4.23: Température dans un barreau de section variable

Dans ce cas le flux de chaleur $\phi_{e}$ à l'extrémité s'écrit: $\phi_{e}=hS(T-T_{a})$, et l'équation d'équilibre s'écrit:

$$\left\{ \begin{array}{c} -\frac{d}{dx}(K(x)\frac{dT}{dx})+\a... ...-K(L)\frac{dT}{dx}(L)=\alpha(L) (T(L)-T_{a})\end{array}\right.$$

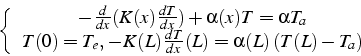
Nous allons traiter avec les programmes précédents 3 cas correspondants à 3 ailettes de section rectangulaire variable. Ces 3 ailettes ont une longueur $L=0.1 m$, une largeur $H=0.2 m$, mais une épaisseur variable telle que:

1. une section $S(x)=H*D(x)$ croissante d'épaisseur $D(x)=0.025+0.050\frac{x}{L}$
2. une section $S(x)=H*D(x)$ décroissante d'épaisseur $D(x)=0.075-0.050\frac{x}{L}$
3. une section $S(x)=H*D(x)$ constante d'épaisseur $D(x)=0.05 m$

L'épaisseur moyenne étant la même pour les 3 ailettes, elles ont un même volume $V=10^{-3} m^{3}$, mais des surfaces d'échange différentes.

Le programme Maple 4.4 ci-dessous donne les paramètres du problème dans le cas d'une convection forcée avec $h=10^{4} W/m^{2}/K$.

programme Maple 4.4: Paramétres pour le calcul de l'ailette à section variable

# Parametres du problème: section rectangulaire
> L:=0.10; H:=0.20;
> dd:=x->0.075-0.050*x/L;
> #dd:=x->0.025+0.050*x/L;
> #dd:=x->0.05;
> h:=10000;Ta:=20;Te:=60;
> S:=unapply(dd(x)*H,x);pp:=unapply(2*(dd(x)+H),x);
> alpha:=unapply(h*pp(x),x);
> K:=unapply(6000.0*S(x),x);
> f:=unapply(alpha(x)*Ta,x);
> ue:=Te: beta:=h*S(L); phi:=h*S(L)*Ta;

En utilisant un maillage de $ne=16$ éléments $\mathcal{P}^{1}$, on obtiens les résultats suivants pour les 3 types d'ailette que l'on a tracé sur la figure (4.24). A titre de comparaison, on a aussi tracé la solution analytique obtenue avec Maple pour le cas 3 (ailette de section constante). Cela nous permet de vérifier que la solution éléments finis $\mathcal{P}^{1}$ avec un maillage de $ne=16$ éléments est suffisamment précise, puisque la solution exacte et la solution approchée sont quasiment confondues.

Figure: Solution $\mathcal{P}^{1}$ pour les 3 sections d'ailette

On constate sur cette figure (4.24) que la température à l'extrémité de l'ailette est la plus faible dans le cas 1, et la plus grande dans le cas 2. Cela peut s'expliquer par une surface d'échange plus grande à l'extrémité de l'ailette dans le cas 1 que dans le cas 2 ( 3 fois plus petite), et dans le cas 3 (2 fois plus petite).

Cependant si l'on calcul le flux de chaleur $\phi=-kS(\frac{dT}{dx})_{x=0}$ évacué par l'ailette, on trouve les résultats suivants:

$$\phi_{1}=178650 W, \phi_{2}=18620 W, \phi_{3}=19350 W$$

ce qui montre que dans ce cas l'ailette la plus efficace est l'ailette 3 de section constante. En effet même si dans le cas 1 la température dans l'ailette est plus faible, et donc le gradient de température plus important, la section en $x=0$ est plus faible que dans le cas 3, et donc globalement le flux est plus petit. C'est exactement le contraire pour l'ailette 2.