Sous-sections

Pour valider le calcul, on va vérifier des propriétés de conservation de la solution. La solution exacte $T_{e}$ vérifie l'équation (2.1). En intégrant cette équation sur le domaine $\Omega=\Omega_{1}\cup\Omega_{2}$ , et en notant que sur $\Omega_{1}$ , il vient:

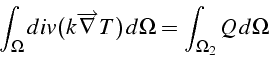
$\begin{displaymath} \int_{\Omega}div(k\overrightarrow{\nabla}T) d\Omega=\int_{\Omega_{2}}Q d\Omega\end{displaymath}$

En utilisant le théorème de la divergence, on obtiens la relation suivante:

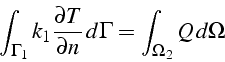
$\begin{displaymath} \int_{\Gamma_{1}}k_{1}\frac{\partial T}{\partial n} d\Gamma=\int_{\Omega_{2}}Q d\Omega\end{displaymath}$

qui traduit le fait que le flux de chaleur évacué par le radiateur est égale à la puissance dissipée par effet joule dans le câble.

Pour la solution approchée $T^{h}$ , on trouve avec FEMLAB

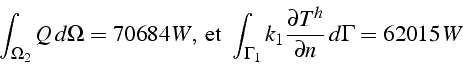
$\begin{displaymath} \int_{\Omega_{2}}Q d\Omega=70684 W, \textrm{\mbox{et\... ..._{1}}k_{1}\frac{\partial T^{h}}{\partial n} d\Gamma=62015 W\end{displaymath}$

soit une différence de 12% pour degrés de liberté. Il faut alors raffiner considérablement le maillage pour ramener cette différence à quelques % (avec un maillage 4 fois plus fin de degrés de liberté, le flux de chaleur vaut et l'erreur est encore de 5%). Cette différence est due à la singularité sur le flux qui se développe sur les angles du radiateur.

Une meilleur stratégie pour augmenter la précision du calcul est alors d'utiliser l'adaptation de maillage, i.e. de raffiner localement le maillage aux endroits ou la solution est la moins précise (i.e. la où le flux de chaleur varie beaucoup). C'est la version 2 du modèle.

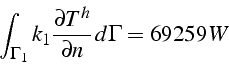
ce qui donne une erreur de 2% pour degrés de liberté.

Pr. Marc BUFFAT
marc.buffat@univ-lyon1.fr
2008-02-28

2.2 Modèle FEMLAB

2.2.1 description du modèle version 1

2.2.2 exécution du modèle version 1

2.2.3 validation du modèle 1

2.2.4 description du modèle version 2

2.2.5 exécution du modèle version 2

2.2.6 validation du modèle 2