suivant: 8.4 Contrainte dans le monter: 8. Contraintes et Multiplicateur précédent: 8.2 Contraintes sur les Table des matières
Considérons le problème de Poisson suivant dans le cercle unité ![]() .
.
avec des conditions aux limites homogènes sur le cercle ![]() de rayon 1:
de rayon 1:
La formulation faible du problème s'écrit:
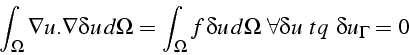
Pour cela on reformule le problème en terme de multiplicateur de Lagrange,
en introduisant une inconnue supplémentaire ![]() : la force supplémentaire
à appliquer au centre. Le problème s'écrit:
: la force supplémentaire
à appliquer au centre. Le problème s'écrit:
Trouver ![]() et
et ![]() tels que:
tels que:
La formulation faible est obtenue en multipliant la première équation
par la fonction test ![]() de
de ![]() et la seconde par la fonction
test
et la seconde par la fonction
test ![]() de
de ![]() :
:
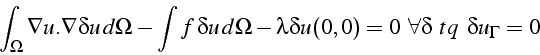
Ce système s'interprète comme les conditions de minimisation de la fonctionnelle:
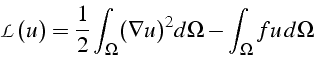
soumise à la contrainte ![]() .
.
On écrit donc que les gradients (par rapport à ![]() ) de
) de
![]() et de la contrainte sont parallèles:
et de la contrainte sont parallèles:
et que la contrainte est vérifiée:
Ce sont les conditions de minimisation de la fonctionnelle ![]() de
de ![]() et
et ![]() suivante:
suivante:
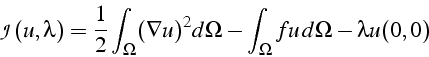
Le multiplicateur de Lagrange ![]() est alors la force à appliquer
en
est alors la force à appliquer
en ![]() pour imposer le déplacement
pour imposer le déplacement ![]() .
.
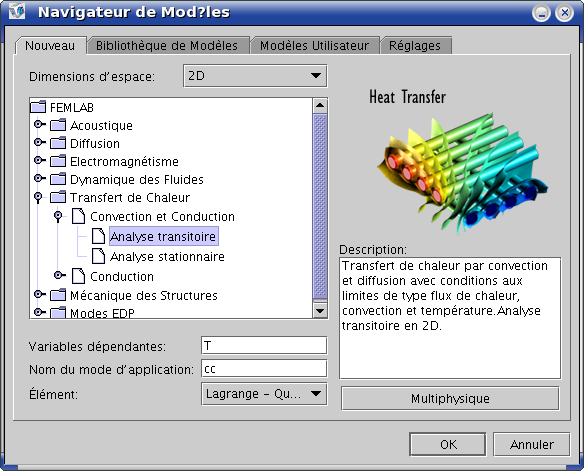
Sous FEMLAB, on introduit un point en ![]() et on impose en ce point
une contrainte
et on impose en ce point
une contrainte ![]() . On sélectionne le mode “Contraintes
faibles” ideal dans le menu Physique->Propriété.
. On sélectionne le mode “Contraintes
faibles” ideal dans le menu Physique->Propriété.
La contrainte faible ![]() est imposée dans le champ “contrainte”,
et FEMLAB introduit automatiquement le multiplicateur de Lagrange
associé
est imposée dans le champ “contrainte”,
et FEMLAB introduit automatiquement le multiplicateur de Lagrange
associé ![]() (noté
(noté ![]() ) et les termes faibles associées:
) et les termes faibles associées:
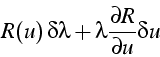
La solution est de la forme suivante:
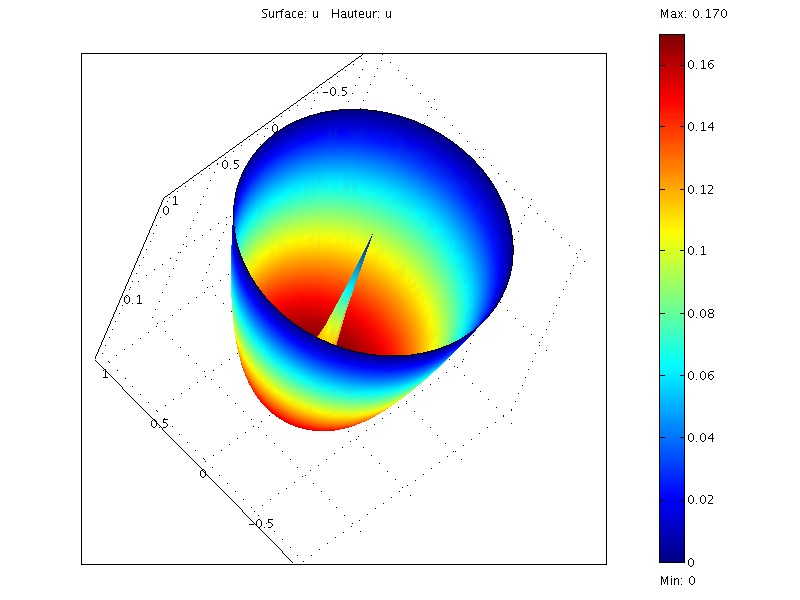
La valeur du multiplicateur ![]() (force à appliquée) est obtenue
avec le menu “post-traitement -> graphique -> point”
et en selectionnant lm1.
(force à appliquée) est obtenue
avec le menu “post-traitement -> graphique -> point”
et en selectionnant lm1.
description du modele FEMLAB (version HTML)