8.4 Contrainte dans le domaine

Soit un champ de vitesse 2D $\overrightarrow{U}=(u_{1},u_{2})$, dans un carré unité $\Omega=[0,1]x[0,1]$ , vérifiant les contraintes suivantes:

1. sur la frontière supérieure $\Gamma_{1}(y=1)$: $\overrightarrow{U}=(1,0)$
2. sur les 3 autres frontières $\Gamma_{0}(y=1,x=0,x=1)$: $\overrightarrow{U}=(0,0)$.

et à divergence nulle: $div \overrightarrow{U}=0$

On veut déterminer parmi tous les champs de vitesse $\overrightarrow{U}$ vérifiant les conditions aux limites précédentes et à divergence nulle, celui qui minimise la fonctionnelle $\mathcal{L}(\overrightarrow{U})$ suivante:

$$\mathcal{L}(\overrightarrow{U})=\frac{1}{2}\int_{\Omega}\lef... ...bla}u_{1})^{2}+(\overrightarrow{\nabla}u_{2})^{2}\right)d\Omega$$

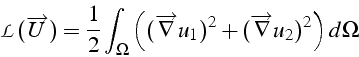
On écrit donc que les gradients (par rapport à $u$) de $\mathcal{L}(u)$ et de la contrainte sont parallèles:

$$<\nabla_{u}\mathcal{L}(\overrightarrow{U}),\delta\overrightarrow{U}>_{\Omega}=<\lambda,div \delta\overrightarrow{U}>_{\Omega}$$

soit

$$\int_{\Omega}\nabla u_{1}.\nabla\delta u_{1} d\Omega+\int_... ...2}}{\partial y}) d\Gamma \forall\delta u_{1},\delta u_{2}$$ (8.4)

Ce sont les conditions de minimisation par rapport à $\overrightarrow{U}$ de la fonctionnelle $\mathcal{J}$ de $\overrightarrow{U}=(u_{1},u_{2})$ et $\lambda$ suivante:

$$\mathcal{J}(u_{1},u_{2},\lambda)=\frac{1}{2}\int_{\Omega}\le... ...d\Omega-\int_{\Omega}\lambda div\overrightarrow{U} d\Omega$$ (8.5)

La minimisation par rapport à $\lambda$s'écrit:

$$-\int_{\Omega}\delta\lambda div\overrightarrow{U} d\Omega=0 \forall\delta\lambda$$ (8.6)

qui est bien équivalent à la condition de divergence nulle $div\overrightarrow{U} =0$

Attention, ce problème de minimisation n'admet pas une solution unique, car le multiplicateur $\lambda$ est définie à une constante arbitraire près. En effet pour un couple solution $(\overrightarrow{U},\lambda)$ des équations 8.4 et 8.6, tout couple $(\overrightarrow{U},\lambda+C)$, $C\in\mathcal{R}$, est aussi solution de 8.4, car :

$$\int_{\Omega}C div\overrightarrow{\delta U} d\Omega=\int... ...{\Gamma}\delta\overrightarrow{U}.\overrightarrow{n} d\Gamma=0$$

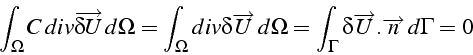
puisque $\delta\overrightarrow{U}$ s'annulle sur le bord (condition de Dirichlet sur $\overrightarrow{U}$), et de 8.6 car:

$$\delta(\lambda+C)=\delta\lambda$$

Il faut donc imposer une contrainte sur $\lambda$, par exemple la valeur en $(0.5,0)$.

En terme d'approximation, si la solution $\overrightarrow{U}$ est un polynôme de degré $k$, la contrainte $div\overrightarrow{U}$ est un polynôme de degré $k-1$, et donc l'interpolation pour $\lambda$ doit être de degré $k-1$.

Ce multiplicateur de Lagrange $\lambda$ s'interpréte comme la pression $p$ du problème de Stokes suivant :

$$\begin{eqnarray*} -\nu\Delta\overrightarrow{U} & = & -\overrightarrow{\nabla}p\\ div\overrightarrow{U} & = & 0\end{eqnarray*}$$

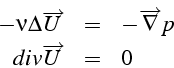
dont la formulation faible s'écrit:

$$\nu\int_{\Omega}\nabla u_{1}.\nabla\delta u_{1} d\Omega+\n... ...}\delta u_{1}+\frac{\partial p}{\partial y}\delta u_{2})d\Omega$$

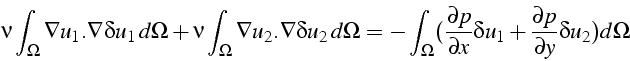
En intégrant par partie le terme de droite, et en tenant compte des conditions aux limites sur $\delta\overrightarrow{U}$, il vient:

$$\nu\int_{\Omega}\nabla u_{1}.\nabla\delta u_{1} d\Omega+\n... ...{\partial x}+\frac{\partial\delta u_{2}}{\partial y}) d\Gamma$$

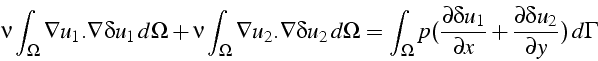
qui est exactement l'équation (8.4) avec $\lambda=p$ et $\nu=1$.

La condition d'incompressibilité $div \overrightarrow{U}=0$ s'interpréte donc comme une contrainte sur le champ de vitesse, et la pression $p$ comme le multiplicateur de Lagrange associé à cette contrainte: i.e. la force à exercée sur l'écoulement pour maintenir la densité constante.

On remarque aussi que pour ce problème de Stokes, la pression $p$ est définie à une constante arbiraire près.

8.4.1 Modèle FEMLAB

Avec FEMLAB, on introduit 3 variables, $u_{1}$ et $u_{2}$ solution d'une equation de Laplace avec les conditions aux limites sur la vitesse, et un multiplicateur de Lagrange $lm$ (forme faible sous domaine) . On introduit la forme faible des équations

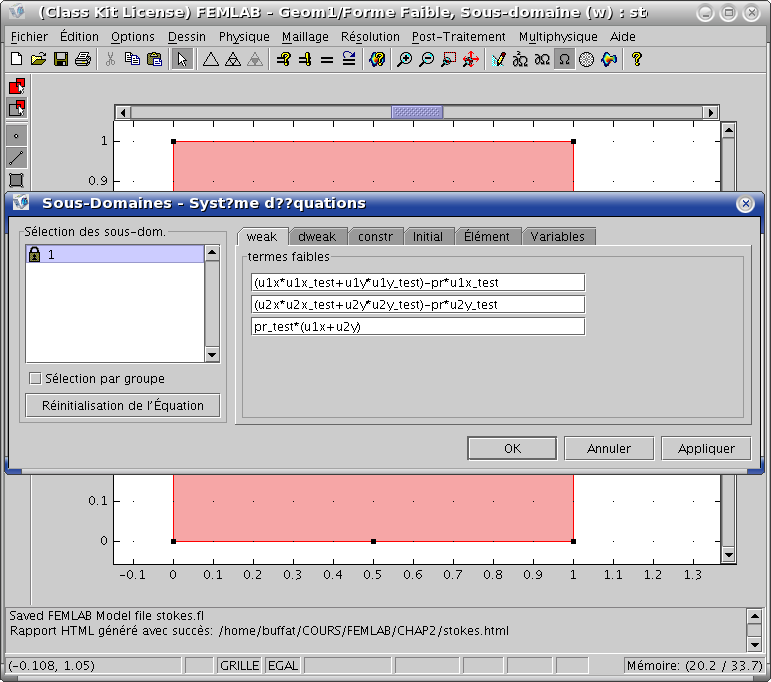
On introduit le point $(0.5,0)$ avec une contrainte $pr=0$ pour fixer le niveau de la pression. La solution est de la forme suivante:

description du modele FEMLAB

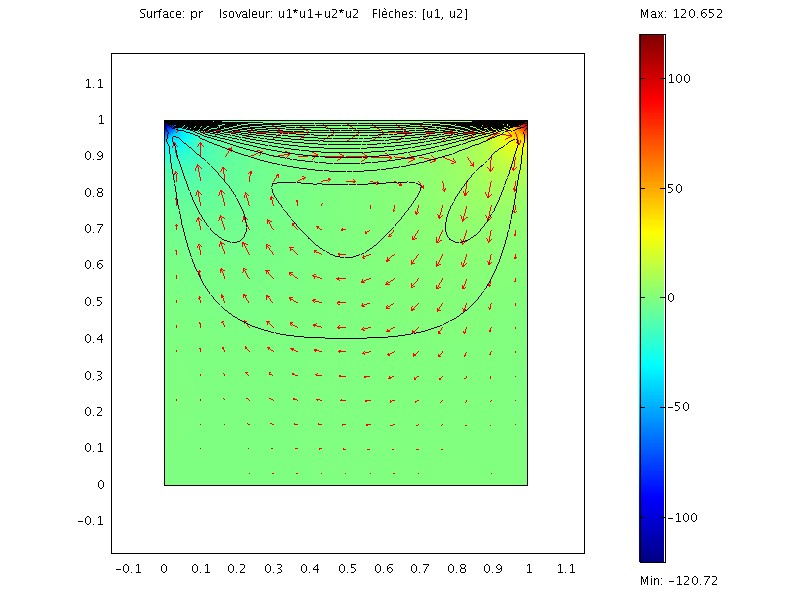
description du modele FEMLAB (version HTML)