suivant: 8.3 Contrainte de force monter: 8. Contraintes et Multiplicateur précédent: 8.1 Introduction Table des matières
Les conditions aux limites de Dirichlet peuvent être interprété comme des contraintes sur la solution. Elles sont donc imposées à travers l'introduction de multiplicateur de Lagrange.
Considérons le problème de Poisson suivant dans le cercle unité ![]()
On interprète la condition aux limites ![]() comme une contrainte.
comme une contrainte.
La formulation variationnelle s'écrit: trouvez ![]() minimisant
minimisant
![]()
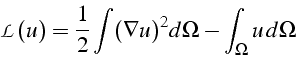
sous la contrainte ![]() .
.
On écrit donc que les gradients (par rapport à ![]() ) de
) de
![]() et de la contrainte sont parallèles:
et de la contrainte sont parallèles:
soit
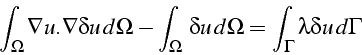
Ce qui correspond à la minimisation de la fonctionnelle
![]()
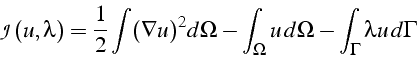
Le multiplicateur de Lagrange ![]() s'interprète donc comme la
valeur de
s'interprète donc comme la
valeur de
![]() sur la frontière permettant
d'obtenir
sur la frontière permettant
d'obtenir ![]() . Le problème d'équilibre associé s'écrit:
. Le problème d'équilibre associé s'écrit:
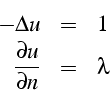
où ![]() est tel que la solution vérifie
est tel que la solution vérifie ![]() .
.
L'intérêt de cette approche par rapport à la condition de Dirichlet
classique est que l'on a accès à la valeur exacte ![]() de
de
![]() ,
alors que la solution élément finie
,
alors que la solution élément finie ![]() fournit uniquement une
approximation
fournit uniquement une
approximation
![]() .
.
Sous FEMLAB, on peut imposer les contraintes sur les conditions aux limites sous deux formes. Pour cela on sélectionne le mode “Contraintes faibles” ideal dans le menu Physique->Propriété.
La forme implicite consiste alors, dans le menu “condition
aux limites”, à introduire la condition ![]() à imposer dans
le champ constr, du tableau Faible (weak)
à imposer dans
le champ constr, du tableau Faible (weak)
FEMLAB introduit automatiquement le multiplicateur de Lagrange associé
![]() (noté
(noté ![]() ) et les termes faibles associées:
) et les termes faibles associées:
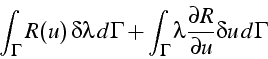
La seconde méthode est d'introduire explicitement le multiplicateur
de Lagrange ![]() sur la frontière
sur la frontière ![]() en ajoutant, dans
le mode multi-physique, une équation faible supplémentaire pour cette
contrainte (Forme Faible, limite). Pour la première équation, on impose
des conditions de Neuman homogène (i.e. par de contribution d'intégrale
de bord dans la formulation), et on introduit dans la seconde équation
les intégrales de bords manquantes:
en ajoutant, dans
le mode multi-physique, une équation faible supplémentaire pour cette
contrainte (Forme Faible, limite). Pour la première équation, on impose
des conditions de Neuman homogène (i.e. par de contribution d'intégrale
de bord dans la formulation), et on introduit dans la seconde équation
les intégrales de bords manquantes:
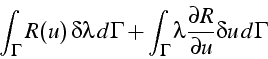
sous la forme: lm*u_test+lm_test*u dans les conditions
aux limites sur ![]() (noté lm).
(noté lm).
La solution calculée à la forme suivante:
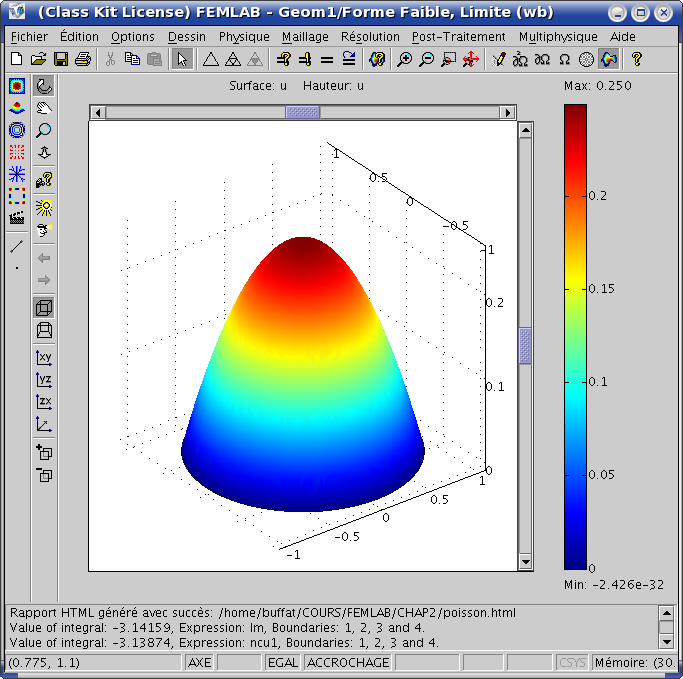
Cette solution est identique à la solution calculée avec des conditions
de dirichlet. La seule différence est qu'avec l'approche des multiplicateurs,
on a accès une meilleur approximation ![]() de
de
![]() .
En effet la solution exacte vérifie
.
En effet la solution exacte vérifie
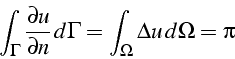
et on vérifie avec FEMLAB que
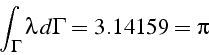
alors que la solution élément finis fournie:
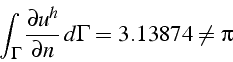
La méthode des multiplicateurs de Lagrange pour les conditions aux limites permet d'avoir accès à une meilleur approximation des fluxs ou des contraintes sur les frontières.
description du modele FEMLAB (version HTML)