8.1 Introduction

La prise en compte de contraintes supplémentaires est un point essentiel dans les applications. Dans la méthode des éléments finis, cette prise en compte se fait à l'aide de multiplicateurs de Lagrange.

On pourra consulter l'introduction suivante sur le multiplicateurs de Lagrange www.slimy.com/˜steuard/tutorials/Lagrange.html

D'un point de vue mécanique, ces multiplicateurs s'interprètent comme des forces supplémentaires appliquées au système.

8.1.1 Un exemple classique: le problème du laitier

Un laitier doit se rendre d'un point $M$ (la laiterie) à un point $C$ (la ferme) pour chercher le lait. Il doit cependant s'arrêter près de la rivière, qui est la courbe $g(x,y)=0$. Quel est le trajet le plus court pour aller de $M$ à $C$ en passant par un point de la courbe $g(x,y)=0$?

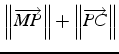Ce qui est équivalent à déterminer le point $P$ de la courbe $g(x,y)=0$ tel que la distance $\left\Vert \overrightarrow{MP}\right\Vert +\left\Vert \overrightarrow{PC}\right\Vert$ soit la plus petite possible. Soit, mathématiquement:

Trouvez le point $P$ tel que $f(P)=\left\Vert \overrightarrow{MP}\right\Vert +\left\Vert \overrightarrow{PC}\right\Vert$ soit minimum sous la contrainte $g(P)=0$

Ce problème admet une solution graphique: on trace les ellipses de foyers $M$ et $C$. Chaque ellipse correspond à une courbe $f(P)=cste$ (la distance d'un point d'une ellipse aux foyers est constance puisqu'on trace une ellipse avec une corde et 2 piquets). Le point $P$ recherché correspond à l'intersection de la plus petite ellipse tangente à la courbe $g(x,y)=0$.

Mathématiquement, cela consiste à écrire qu'en $P$ la tangente à l'ellipse $f(P)=cste$ est parallèle à la tangente à la courbe $g(P)=0$. Ces deux vecteurs sont parallèles si:

$$\overrightarrow{grad} f(P) =\lambda \overrightarrow{grad} g(P)$$ (8.1)

où $\lambda$ est une facteur multiplicateur, appelé multiplicateur de Lagrange.

Les 2 équations 8.1 et la contrainte $g(P)=0$ forment un système de 3 inconnues $(x,y,\lambda)$ que l'on résout pour avoir la solution. Par exemple, pour $M=(0,0)$, $C=(1,0)$ et $g(P)=y-cos(x)$, la solution (obtenue avec Maple) s'écrit:

$$x=1.119, y=0.436, \lambda=1.654$$

et correspond à l'ellipse $f(x,y)=1.654$

De façon générale, la condition de minimisation d'une fonction $f$ sous contrainte $g=0$ impose que le gradient de la fonction à minimiser $f(X)$ soit parallèle au gradient de la contrainte $g(X)=0$:

$$\overrightarrow{\nabla_{X}}f = \lambda\overrightarrow{\nabla_{X}}g$$

$$g(X) = 0$$ (8.2)

8.1.2 La méthode des multiplicateurs de Lagrange

La relation 8.2 et l'équation de la contrainte peut aussi s'interpréter comme la condition de minimisation de la fonctionnelle $F(X,\lambda)$ de $X$ et $\lambda$ suivante:

$$F(X,\lambda)=f(X)-\lambda g(X)$$

dont le gradient vaut:

$$\overrightarrow{\nabla_{X}}F = \overrightarrow{\nabla_{X}}f-\lambda\overrightarrow{\nabla_{X}}g$$

$$\overrightarrow{\nabla_{\lambda}}F = -g(X)$$ (8.3)

La condition de minimisation de $F(X,\lambda)$ équivaut donc aux équations (8.2).