suivant: 6.10 Méthode de Krylov monter: Solveur linéaire itératif précédent: 6.8 Méthode de décomposition Table des matières
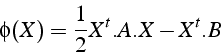
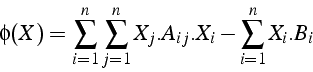
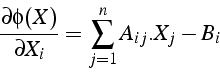
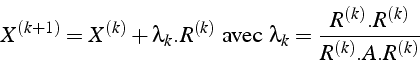
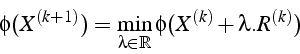
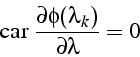
La convergence de la méthode de gradient dépend du conditionnement
de la matrice ![]() . Plus le conditionnement augmente, et plus la vitesse
de convergence diminue.
. Plus le conditionnement augmente, et plus la vitesse
de convergence diminue.
Pour améliorer la convergence, on préconditionne le système en multipliant
par une matrice de préconditionnement ![]() :
:
telle que
![]() , i.e. que
, i.e. que ![]() est le même
spectre de valeurs propres que
est le même
spectre de valeurs propres que ![]() (
(
![]() ).
).
La direction de descente ![]() est telle qu'elle est orthogonale
à la direction précédente
est telle qu'elle est orthogonale
à la direction précédente ![]() :
:
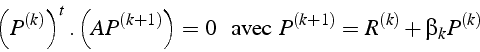
d'où:
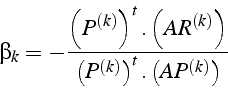
L'itération de gradient conjugué s'écrit:
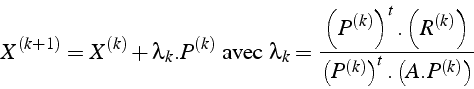
La convergence de la méthode est quadratique, i.e. en
![]()
englishméthode de gradient sous Maple